从RC电路的充电谈起
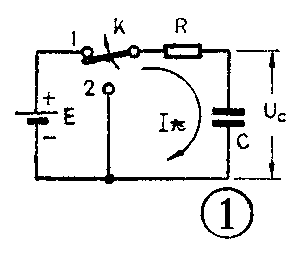
图1是一个RC串联电路,当开关扳到“1”时,电路和电源接通,电源就对电容C充电。假定开始时电容器上没有电荷,也就是U\(_{C}\)=0,那么开关合上的瞬间充电电流最大,其值为
I\(_{充}\)=\(\frac{E}{R}\)
随着时间的增长,电容器上积累的电荷逐渐增加,电压也逐渐升高,充电电流就逐渐减小。经过一段时间之后,电容器上的电压U\(_{C}\)便等于电源电压E,这时充电电流等于零,充电过程也就结束。在充电过程中,电容器上电压的变化可以用一条曲线来表示,见图2。
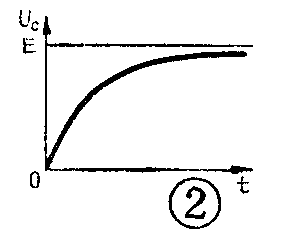
那么究竟要经过多少时间才能使电容器上的电压充到等于E呢?充电时间都是和哪些因素有关系呢?
我们知道,电容器的容量越大,能储存的电荷就越多,因此充电时间的长短和电容器的容量有关:容量越大,充电时间就越长;相反,容量越小,充电时间就越短。另外,电路中的电阻也和充电时间有关,电阻阻值越大,电路的充电电流就越小,电荷积累得就慢,充电时间就长;电阻阻值越小,充电电流越大,充电时间就短。因此充电时间既和电容容量有关,又和电阻阻值有关,电容和电阻的数值越大,充电时间就越长。
一把特殊的尺子——时间常数
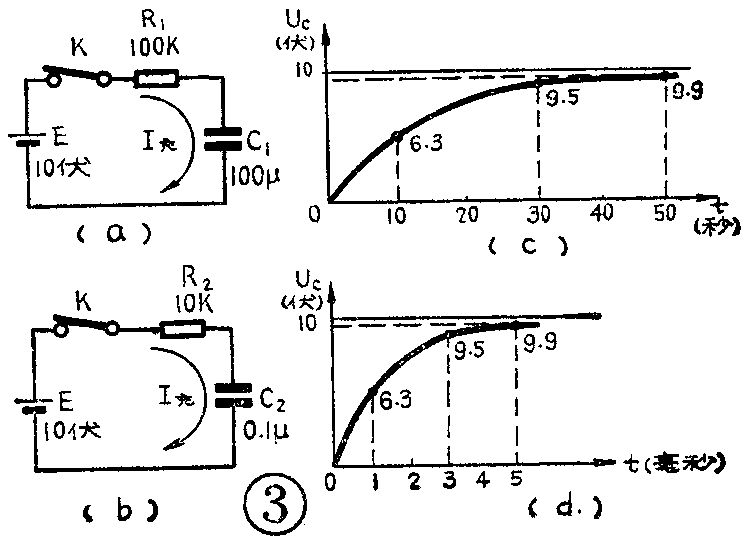
以上我们定性地分析了RC的数值和充电时间的关系,下面我们再进行定量地分析。假定有两个RC电路(见图3a、b),一个电路的RC数值较大,另一个较小,把它们都接到10伏的电源上,通过测量可得到它们的充电曲线(见图3c、d)。从曲线可以看到,图3a要经过50秒才使U\(_{C}\)达到9.9伏,而图3b却只要5毫秒就能达到9.9伏。这两个电路形式上完全相同,只是RC的数值不同,结果充电时间差别很大。那么它们的充电过程有没有共同的规律呢?在图3a中,R1=100K,C\(_{1}\)=100μF,如果求出RC的乘积:
R\(_{1}\)C1=100×10\(^{3}\)×100×10-6=10欧·法
同样对图3b的电路求得:
R\(_{2}\)C2=10×10\(^{3}\)×0.1×10-6=1×10\(^{-3}\)欧法
再来看看RC乘积的单位是什么:
欧·法=\(\frac{伏}{安}\)·库;伏=\(\frac{安·秒}{安}\)=秒
原来它的单位就是时间单位“秒”。因此,
R\(_{1}\)C1=10秒,R\(_{2}\)C2=1毫秒。
如果拿RC乘积的秒数和充电曲线对照,就可以发现它们有共同的规律:经过一个RC的时间后,它们都被充到6.3伏,三个RC时间后都充到9.5伏,五个RC时间后都充到9.9伏。这就是说,它们充到相同高度所用的时间被它们各自的RC乘积去除,所得的商相等,因此可以用RC的乘积作为衡量它们的充电时间的一把特殊的尺子,只要知道了RC的乘积,充电充到一定高度所用的时间也就知道了。由于RC乘积的单位是秒,因此就把它叫作“时间常数”,通常用τ来表示。
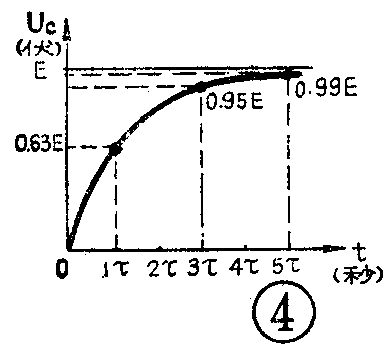
用时间常数τ这把尺子,可以找出所有RC串联电路充电规律的通用曲线,见图4。从图4可以看到,经过一个τ,电容被充到电源电压的0.63倍,即U\(_{C}\)=0.63E,在3τ时达到0.95E,5τ时达到0.99E。不管τ的大小如何,也不管电源电压E的大小如何,都是按这一规律充电的。
把图1中的开关从1扳到2时,电容C通过电阻R放电。刚开始的瞬间放电电流最大,它等于
I\(_{放}\)=-UCR
式中的负号表示放电电流和充电电流方向相反。
那么放电时的规律又是怎样的呢?
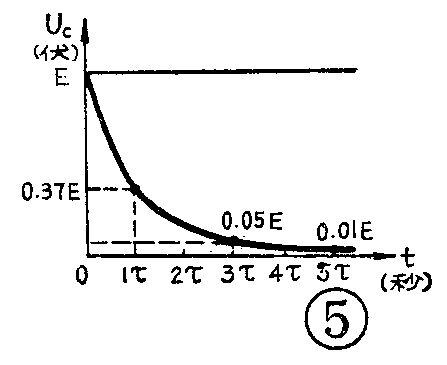
研究后发现,把RC电路的充电曲线倒过来就是它的放电曲线,而且同样可以用时间常数τ作为衡量放电时间长短的尺子,如图5。从图5看到,时间为1τ时,电容上的电压降到电源电压的0.37倍(放掉了0.63倍),即U\(_{C}\)=0.37E,3τ时UC=0.05E,5τ时U\(_{C}\)=0.01E。因此在研究分析RC电路放电的规律时,同样可以用时间常数τ这把尺子和这条通用曲线。
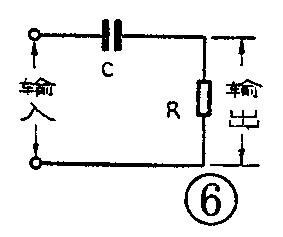
微分电路与耦合电路
由以上分析可以知道,在电容器充放电过程中,电容上的电压和先放电电流从起始值变到某个一定的数值所需要的时间又决定于电阻R和电容C的乘积,即时间常数τ。了解了这一点以后,有些现象就很容易理解了。例如,脉冲电路里常用的微分电路和耦合电路,在形式上完全相同,见图6,但它们的作用不同,原因就在于它们的时间常数不同。当图6中的R=10K,C=0.01μF时,设它的时间常数为τ\(_{1}\),则τ1=RC=0.1毫秒。这时我们在输入端加进脉冲幅度为10伏、宽度为1毫秒的矩形脉冲(见图7a),分析一下输出电压的波形。脉冲电压在t\(_{1}\)时加到输入端,这时电容C开始充电,经过1τ=0.1毫秒,UC=6.3伏;3τ=0.3毫秒,U\(_{C}\)=9.5伏。由于脉冲宽度为1毫秒,远远大于时间常数τ,因此到1毫秒时UC已基本等于10伏。接着在t\(_{2}\)时放电,经过1τ=0.1毫秒,UC=3.7伏;3τ=0.3毫秒,U\(_{C}\)=0.05伏,1毫秒后已基本等于零。电容上的电压变化如图7b。
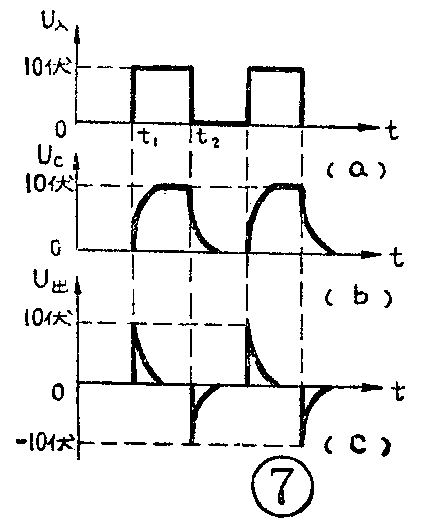
在电容充电时电阻R上的电压U\(_{R}\)=U-UC,也就是用图7a的矩形脉冲电压减去图7b的U\(_{C}\)充电电压,得到UR的电压变化波形如图7C。可见在输入为正脉冲时U\(_{R}\)是个正的尖脉冲。在电容放电时,由于UC+U\(_{R}\)=0,因此UR=-U\(_{C}\)。也就是UR的变化波形和U\(_{C}\)正好相反,可见在输入电压从正变为零时UR是个负的尖脉冲。这种输入矩形脉冲后在输出端能产生交替的正负尖脉冲的电路正是微分电路。
现在保持输入脉冲周期T不变而把R和C的数值加大,例如R=100K,C=0.1μF,则τ\(_{2}\)=RC=10毫秒。当电路输入正脉冲对电容C充电时,因为τ2很大,电容C上的电压U\(_{C}\)刚充上一点点,输入脉冲就从正变成了零(见图8a、b),又因为UR=U-U\(_{C}\),所以正脉冲的绝大部分电压都加到电阻R上(见图8c)。当输入脉冲从正降到零时,电容C放电,因为UC数值很小,根据U\(_{R}\)=-UC,所以U\(_{R}\)也很小但方向相反。从图8c看到UR的波形是和输入脉冲波形(图8a)基本相同的,也就是说,输入脉冲经过这个电路传送到了输出端,因此这时它是一个耦合电路。总之,在脉冲周期T不变的情况下,由于τ\(_{1}\)<<T,电路是微分电路;τ2>>T,电路则变成了耦合电路。
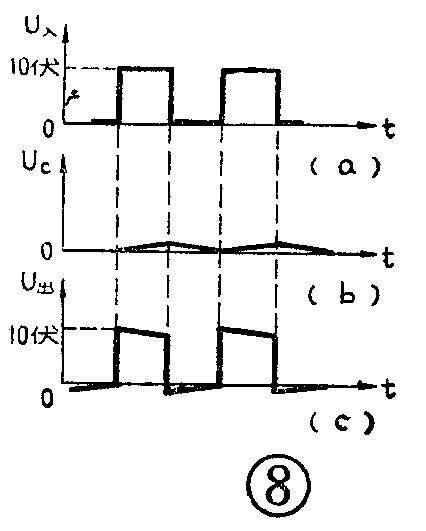
另一种情况,如果保持电路的形式和RC的数值不变,即保持电路的时间常数τ不变,而使输入脉冲的周期T变化,同样,只要是τ<<T,电路就起微分作用;而当τ>>T时,电路就起耦合作用。有些初学者对同一个形式的电路有时是耦合电路,有时又是微分电路,往往感到不易理解,有了时间常数的概念,它们两者就很容易区别了。
用万用表检测大电容
我们再举一个用万用表检测大电容的例子,这也和时间常数有关。把万用表放在测电阻的“×1K”或“×10K”档上,用表笔接电容器的两个电极,如果表笔搭上电极的瞬间表针偏转很大,以后又渐渐返回到起始点附近,就可以断定这个大电容基本上是好的。这是什么原因呢?原来用万用表测大电容的电路就是一个RC由联电路(见图9)。这种电路的时间常数τ很大,充电时间长,所以从表针上可以看到充电电流缓慢的变化。电容器容量越大,充电时间就越长。随着电容器上电压的增加,充电电流逐渐减小,表针也就渐渐返回到起始点。用这种方法不能判断小容量电容器的好坏。因为在测小容量电容时,由于τ的数值很小,只有几十毫秒甚致更短,表针还没来得及摆动充电电流就已降到零,所以就看不到表针的偏转或者只是微微颤动一下就停止了。
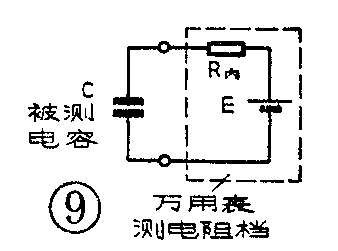
那么为什么一定要放在“×1K”或“×10K”档上呢?因为万用表的欧姆档开关在不同的位置上内阻是不同的,“×1”或“×10”档内阻很小,“×1K”或“×10K”档的内阻很大。所以当开关放在“×1K”或“×10K”档上测电容器时,由于时间常数τ大,充电时间长,可以看到表针的摆动。而在“×1”或“×10”档上,因为τ很小,充电时间短,表针稍一摆动就回到了起始点。所以用这种方法测试大电容器的好坏时,都是放在高阻量程上,这是为了得到较大的时间常数,使表针摆动明显。(方波)