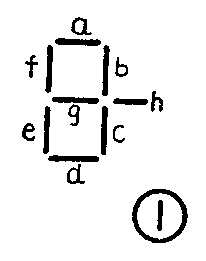
荧光数码管的数码由八段笔画组成,见图1。这些笔画是荧光数码管的阳极。只要控制各笔画的电压,使需要发光(点燃)的笔画接正电压,不需要发光的接0伏,就能显示某一数字。例如,若给图1中的a、b、c、d、e、f各段接正电压,使它们同时发光,则将显示数字“。
怎样控制各段的电压以显示不同的数字呢?这就需要设计一套译码电路(叫作译码器)。设计译码器可以用列式法,也可以用卡诺图化简法。本刊以前介绍过,卡诺图化简法具有规律性强等优点,所以我们这里只介绍卡诺图化简法。此外,这样作也是为使大家进一步熟悉卡诺图的应用提供一个实例。
译码器的作用
在介绍如何设计译码器之前,先谈谈译码器的作用。数码管的译码器接在8421编码的十进制计数器和数码管之间,见图2。译码器的作用是把十进制计数器的不同状态(代表着不同的数字)变换成与十进制数相对应的高电平,送到数码管的某些笔画段上,使这些笔画段点燃,从而显示出相应的数字。
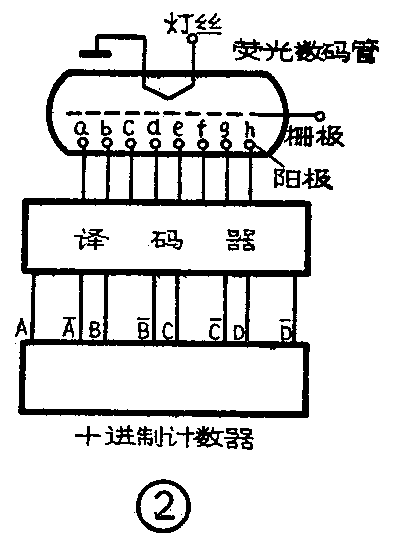
十进制计数器由四个双稳态触发器构成,每个触发器都有两个输出端,如A和A-、 B和B-等等(见图2)。而且这两个输出端对地的电压总是一高一低,如A高则A-低,反之,A-高则A低。这实际上代表着触发器的两种不同的稳定状态。我们令输出端A、B、C、D为高电平时,触发器的状态用“1”表示,A--、C-、D-为高电平时,触发器的状态用“0”表示,则图2所示的四个触发器可以有十六种不同的组合状态,见表1。我们又令0000~1001这十种组合状态代表0~9十个数字(这十个数字和它们的状态编号正好吻合),这就把计数器的状态和数字联系起来了,也就是说,四个触发器的每一种组合状态应当在数码管上显示哪一个数字也就清楚了。从1010~1111这六种组合状态在十进制计数器中不可能出现(因为在十进制计数器内部有反馈,每当第10个脉冲输入时,计数器就反馈为0),所以把它们叫作禁止项。
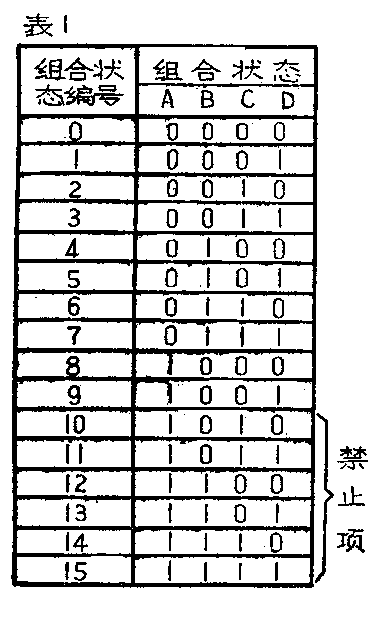
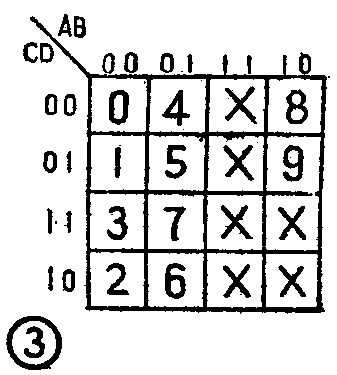
表1也可以画成卡诺图的形式,如图3所示。图3所示卡诺图的意义和表1完全对应,其中填写“X”的方格代表禁止项。有了图3所示的卡诺图,就为用卡诺图化简法设计译码器提供了参考矩阵。
下面我们再看荧光数码管。表2列出了荧光数码管中发光的笔画与字形的对应关系。填1的段表示发光,填0的段表示不发光。由这个表可以清楚地看出每一个笔画段需要在显示哪些字形时发光。例如a段,当需要显示数字0、2.3、5、6、7、8、9中的任意一个时,它都要发光。这就是说,当计数器处于上述数字的任一状态时,通过译码器传送到a段的电平都必须是高电平。图3和表2清楚地表明了译码器的输入和输出的关系,译码器的设计就是根据这种关系来进行的。

译码器的设计
我们仍以数码管笔画的a段为例,说明译码器的设计过程。前边谈到,在显示数字0、2、3、5、6、7、8、9当中的任意一个时,a段都需要发光。根据这个前提,就可以画出代表a段发光的卡诺图,见图4。可以把图4和图3对照来看,图4中,凡需要a段发光的数字所在的方格均填1,不需要发光的则填0,这样就把需要使a段发光的数字和计数器的相应组合状态结合起来了。图中的“X”仍代表禁止项。在图4所示的卡诺图上,把一些方框圈起来合并(即运用卡诺图化简法),就可以列出表示a段发光的最简逻辑表达式了。列式之前,先说明两个问题:
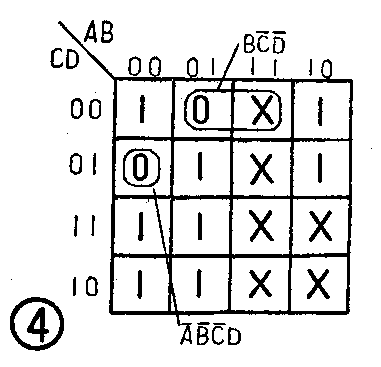
一、化简的时候,既可以合并填1的方格,也可以合并填0的方格。合并填1的方格可以列出需要a段发光的最简逻辑表达式;合并填0的方格则可以列出不需要a段发光的最简逻辑表达式,两者只差一个非号。究竟是合并填1的方格,还是合并填0的方格,则由具体情况来定,哪一个简单,则合并哪一个,对图4来说,显然合并填0的方格较简单。
二、禁止项也可以参加化简。因为禁止项是不可能出现的,所以它们参加化简,并不影响逻辑功能,却能使逻辑表达式更为简单。例如在图4中,数码4所在位置的方格填有0,表示数码4不需要a段发光。由于它周围都不是填0的方格,根据卡诺图化简法,只能把它自己圈起来,于是得到代表这个方格的逻辑表达式A-BC-D-。但是,它右边是一禁止项,可以把它和这一禁止项圈起来,得逻辑表达式BC-D-。BC-D-式中没有因子A,表明A可以为0,也可以为1。当A=0时,BC-D-就代表A-BC-D-,而当A=1时,它就代表ABC-D-。由于ABC-D-这一禁止项不可能出现,所以BC-D-实际只代表A-BC-D-,但BC-D--BC-D-简单。
图4所示的卡诺图,对0化简以后得到的最简逻辑表达式为
F-\(_{a}\)=A-B-C-D+BC-D-
该式的意义是,当计数器的状态为A-B-C-D(也就是A、B、C、为0, D为1时)或为BC-D-时,a段不需要发光,就是a段不应加高电平。根据这个式子,就可以画出a段应当加高电平的译码电路。
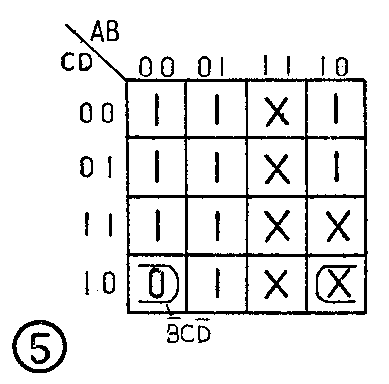
再举一个C段的例子。由表2可见,当显示数码0、1、3、4、5、6、7、8、9中的任意一个时,C段都要发光,由此便可得到C段的卡诺图,如图5所示,化简后为
F-\(_{c}\)-CD-
其它各段的化简过程不再详述(关键是根据表2填写卡诺图),读者可自行推导。下面直接给出各段化简后的逻辑表达式:
F\(_{b}\)=B-+BC-D-+BCD
F-\(_{d}\)=BC-D-+BCD+A-B-C-D-
F-\(_{e}\)=D+BC-D-
F-\(_{f}\)=CD+A-B-C-D+A-B-C
F-\(_{g}\)=A-B-C-+BCD
F\(_{h}\)=BC-D-
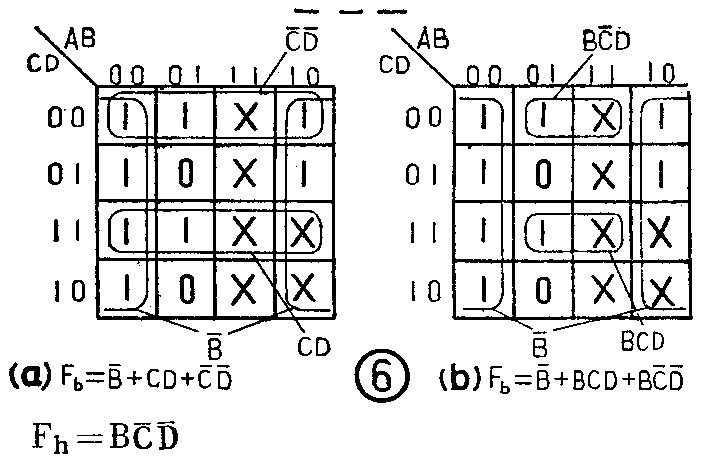
应该特别指出,按卡诺图化简法化简所得到的逻辑表达式,从每一段来说,可能是最简式,但从整个译码器的逻辑结构来说,不一定是最简的。因此,各段化简后,应对简化的逻辑表达式进行综合分析,考查,反复推敲,找出尽可能多的公共项。公共项越多,整个逻辑电路的结构就越简单。为了求得尽量多的公共项,就要对每段化简后的逻辑表达式进行修正。以b段为例,从卡诺图化简法本身来看,应当按图6a的圈法化简,化简后的逻辑表达式为
F\(_{a}\)=B-+CD+C-D-
这个式子单从b段来看是最简的,但从整体来看,因为在其它发光段中有公共项BCD和BC-D-,所以这种圈法并不合理,而以圈6b所示的圈法化简才是合理的。因为这样可以省去CD和C-D-两个与门,而从公共与门BCD和BC-D-中各多引出一个端子就可以了。
如果我们采用的器件是与非门而不是与门和或门的话,各段的逻辑表达式还需用逻辑代数变换成如下的形式:根据这些逻辑表达式怎样画出译码器的逻辑电路图呢?首先要找出这些逻辑表达式中都包含哪些独立的与非门(其中公共项即重复的只需列出一个),结果发现共有六个,它们是A-B-C-D、BC-D-、BCD、A-B-C、CDA-B-C-,把这六个与非门画出来,见图7。然后再从这六个与非门中引出相应的端子,组成能使各段发光的逻辑电路。例如,由于,F\(_{a}\)=A-B-C-D·BC-D-,所以就由与非门A-B-C-D和BC-D-各引出一个端子,作为图7中与非门1的输入端,与非门2的输出端便是Fa。其它各段电路画法依此类推。
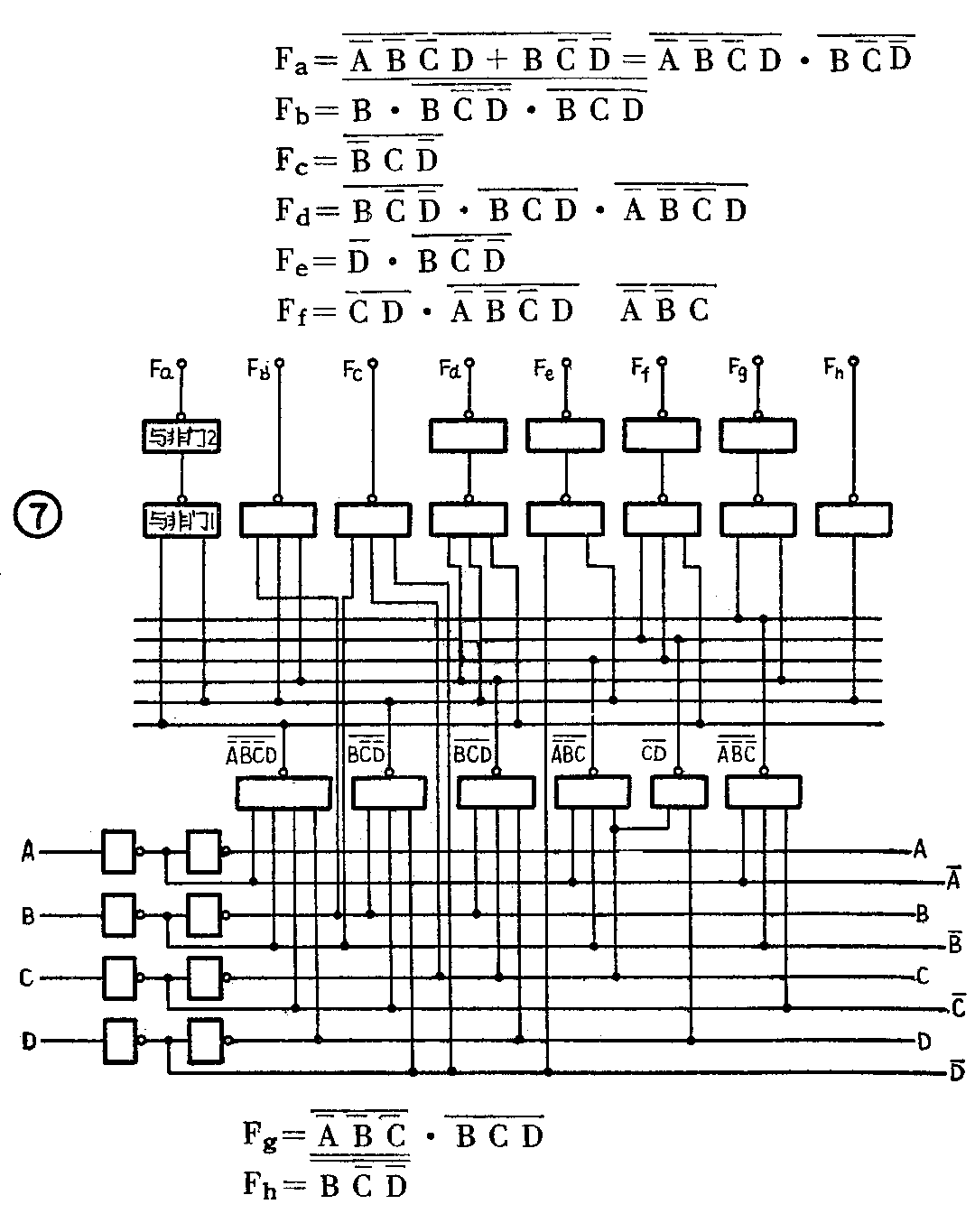
逻辑电路画好以后,还需要进行验证,看看是否有误。我们举数字0为例,说明验证方法。由表1可知,当计数器的状态为0000时,它代表数字0,这时数码管就应当显示0,也就是应当使a、b、c、d、e、f各段发光,g、h、段不发光。计数器状态为0000,说明A、B、C、D均为低电平;而A-B-C-D-均为高电平。由此便可得到A-B-C-D=1、BC-D-,于是F\(_{a}\)便为1,即Fa为高电位,因此a段点燃。用同样的方法也能得知F\(_{b}\)、Fc、F\(_{d}\)、Fe、F\(_{f}\)这时也都为高电位,而Fg、F\(_{h}\)则为低电位。这就证明数码管显示的确实是数字0。其它数字也可以用此法验证,这里就不详述了。需要说明,由于一个数码管只能显示0~9十个数字,所以每个数码管和与其相连的一套电路只能代表多位数字中的一位,如个位、十位等等。若需要显示多位数字。则相应需要多套电路。详细情况这里就不介绍了。(求真)