万用表直流电压和直流电流的测量误差

使用万用表测量晶体管电路的直流电压和直流电流时，往往会发生一些怪现象，使初学者迷惑不解。

图1是一个普通晶体管放大器，用万用表测得晶体管发射极电压V\(_{e}\)=1.8V，基极电压Vb＝2.06V。由于V\(_{be}\)=Vb-V\(_{e}\)，根据测得的数值，则Vbe=2．O6V－1.8V=0.26V。我们知道，硅管的b\(_{e}\)结导通电压Vbe＞0.5V，而图1中3DG\(_{4}\)（硅管）的Vbe只有0.26V，因此它应该处于截止状态。可是，如果晶体管截止， R\(_{e}\)上的电压Ve=1.8V又是从哪里来的呢？这是一个怪现象。下面再看图2。图2中的电流表先后分别串联到晶体管的发射极和集电极电路中，结果得到这样一组数据：I\(_{c}\)=1.75mA，Ie=1.45mA。本来在晶体管电路中应该满足I\(_{e}\)=Ic＋\(_{I}\)b，即I\(_{c}\)＜Ie，而测出的数据却是I\(_{c}\)＞Ie这又是一个怪现象。

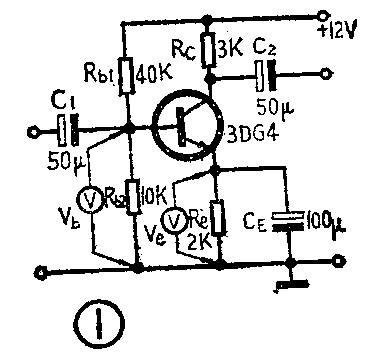
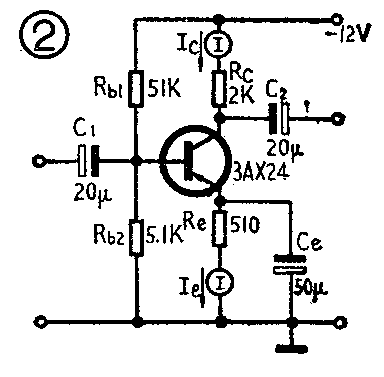
出现这些怪现象，是电路有错误吗？不是。是晶体管的性能不良吗？也不是。一般说来，这些怪现象的产生，是由于万用表的测量误差引起的。下面我们就以国产MF9型万用表为例，具体分析测量误差产生的原因。

图3是国产MF9型万用表直流电压和直流电流档位的简化电路图，这是一般万用表常用的电路型式。

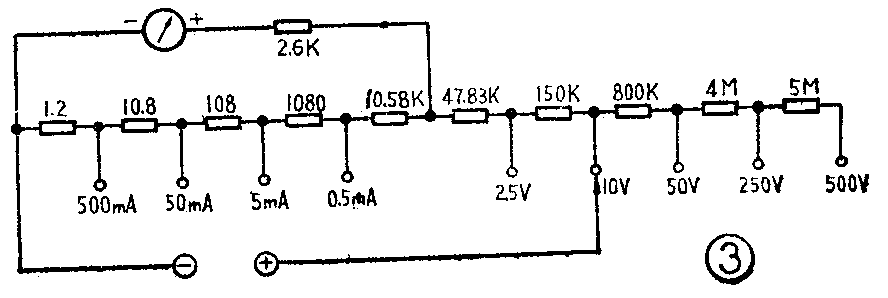
我们在测量电压时，总是把电压表并联到被测电路上，因此电压表对被测电路有分流作用。分流作用的大小和电压表的内阻（78笔两输入端电阻）有关。根据电阻串并联公式可由图3计算出2.5V档内阻

由上面求出的数值不难看出，电压表的内阻与档位的电压值成正比，一般称二者的比值为直流电压档的灵敏度，用KΩ／V表示。对于每一种表，它是一个特定的常数，也是一个质量指标，一般都在万用表的表面给出。例如国产MF9型及500型万用表，灵敏度都是20KΩ／V。这个比值可以用电压的任何一档求出，如10V档的r\(_{1}\)0=200KΩ，则灵敏度为200KΩ／10V=20KΩ／V。各档求出的结果都相同。反过来，知道了灵敏度，也可以很方便地求出各个档位的内阻。如MF9型万用表250V档的内阻r250=20KΩ／V×250V= 5MΩ。

通过上面的分析可知，（1）万用表电压档的内阻是一个可以求出的有限值；（2）内阻的大小随档位电压值而变化，档位电压值越小，内阻越低。

现在我们再回到图1的问题上来。首先我们用计算的方法求出基极电位V\(_{b}\)和发射极电位Ve的值。在β较大时，I\(_{b}\)很小，可忽略不计，所以基极电压就等于Rbl、R\(_{b2}\)的分压，即Vb=12V×10K／（40K＋10K）=2.4V，发射极电压V\(_{e}\)= Vb-0.6V＝2.4V－0.6V=1.8V。下面我们再分析为什么计算值和测量值不符。当我们用2.5V档去测量发射极电压V\(_{e}\)时，就把电表内阻r2·5（50KΩ）并联到R\(_{e}\)（2KΩ）两端，这就改变了发射极电阻的数值。设改变后的发射极电阻为R′e，则R′\(_{e}\)=50KΩ×2KΩ／（50KΩ＋2KΩ）≈2KΩ。可见发射极电阻变化不大，可忽略，因此发射极电压的测量值与计算值基本相符（均为1.8V）。而在测量Vb时，由于r\(_{2·5}\)与Rb2并联，得R′\(_{b2}\)=50KΩ×10KΩ／（50KΩ＋10KΩ）=8.3KΩ。R′b2与R\(_{b2}\)相比，变化较大，Rbl将与R′\(_{b2}\)重新分压，结果得V′b=12V×8.3KΩ／（40KΩ＋8.3KΩ）=2.06V，这就是电表测出的数值，这个值与原计算值（2.4V）就不相符了，测量误差就是这样引起的。

由于在测量V\(_{b}\)的瞬间，Vb降低到V′\(_{b}\)，电路已工作在另一种状态，Ve当然也要随之降低。但当把表笔从基极拿开再去测量V\(_{e}\)时，Vb又恢复了原来的状态，因此V\(_{e}\)也恢复了正常值。由此可见，在分头测量Vb和V\(_{e}\)时，晶体管实际上是工作在两种不同的状态，用其中一个有测量误差的状态下的Vb值减去另一个测量误差很小的状态下的V\(_{e}\)值，这就造成了Vbe=0.26V的怪现象。

为了减小电压的测量误差，必须使电表内阻r远远大于被测两点间的等效直流电阻。因此在测量的时候，应根据晶体管电路的特点，正确地选择测试点，尽量测低电阻上的电压，而避免测高电阻上的电压。例如图1电路可根据V\(_{b}\)＝Ve＋V\(_{be}\)，测出Ve及V\(_{be}\)求出Vb，而不必去直接测V\(_{b}\)。在必要时，也可采用提高电压档位的办法来增加电表内阻r。如在图1中若采用10V档测量，r10=200KΩ，则满足r\(_{l}\)0》Rb2，R\(_{b2}\)与r10并联后数值变化很小，因此V\(_{b}\)的测量误差也就很小。所选电压档位越高，内阻r越大，由r引起的测量误差就越小。但是，由于电表表面的刻度是按档位的满度值校准的，指针偏转的角度越小，刻度指示误差越大，所以两种情况要兼顾。

测量电流时，必须把电流表串联到电路中，这就要求电流表相对于被测电路来说，具有极低的内阻，以减小它对被测电路工作状态的影响。附表列出了国产MF9型万用表电流档各档的内阻数值，它们也是随档位而变化的量。

下面我们具体分析电流档内阻对测量结果的影响。在图2中，我们先把电表串联到集电极电路中，档位选在5mA。由附表可知，这时电表内阻为120Ω。这个电阻和负载电阻串联、得R′\(_{c}\)=2KΩ＋0.12KΩ＝2.12KΩ。显然，因为负载电阻变化不大，Ic的变化也不会很大，所以流过电表的电流与不加电表时电路中的电流误差较小，可忽略。而在测量I\(_{e}\)时，电表串联到发射极电路，则R′e＝510Ω＋120Ω＝630Ω，显然，R′\(_{e}\)比Re大。发射极电阻变大后将使V\(_{e}\)的值升高。由于基极电位取决于Rbl、R\(_{b2}\)的分压，基本上是固定的，根据Vbe=V\(_{b}\)-Vc，则V\(_{e}\)升高将引起Vbe下降，从而使I\(_{b}\)下降，并导致Ic和I\(_{e}\)也下降。因此，测量Ie的瞬间，由于电流档内阻的影响，电路将工作于另一种状态，这时测出的I\(_{e}\)值就会较正常值低，以致得出Ic＞I\(_{e}\)的荒谬结果。

为得到尽量小的电流测量误差，必须使电表内阻r远远小于被测电路的等效直流电阻。因此和测量电压时一样，测量电流时也需要选择合适的测试点。不过测量电流时应选被测电路直流等效电阻较大的测试点，这一点和测量电压时正好相反。例如在测量晶体管工作电流时，把电表接在集电极电路中测量I\(_{c}\)要比接在发射极电路中测量Ie误差小得多。必要时也可采用增大量程的方法减小电表内阻。如在图2中，若用50mA去测量I\(_{e}\)，由于电表内阻只有12Ω,则对测量的影响将会大大减小。当然也要注意读数太小时刻度误差将会增大。（刘铁夫）