两个相邻最小项的合并方法
将逻辑表达式搬上卡诺图以后,就要应用卡诺图进行化简了。化简的过程,就是在卡诺图上合并最小项的过程。那么,什么叫最小项呢?卡诺图中任何一个方格都代表着一个确定的乘积项,例如在图8所示的卡诺图中,A、B的01列和C、D的11行交叉的方格就代表着乘积项A-BCD,同理, A、B的01列和C、D的10行交叉的方格则代表着AB-CD-。这些乘积项有两个共同的特点;第一,它们都包含了卡诺图的全部变量;第二,这些变量不是以原变量的形式出现,就是以反变量的形式出现,而且只出现一次。对于这样的乘积项,我们就叫它最小项。
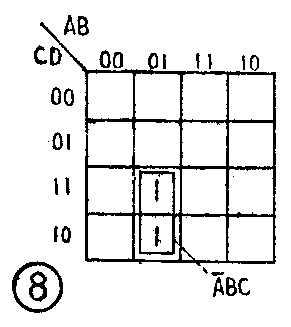
知道了什么叫最小项以后,我们再介绍它的合并方法。所谓合并,实际上是利用卡诺图上最小项之间的某种关系,直接写出代表这些最小项的最简逻辑表达式。从图8所示的四变量卡诺图的结构可知,它的水平变量A、B和垂直变量C、D都是按00、01、11、10的规律变化的,这种变化规律就使相邻的两行之间必有一个变量互补,相邻的两列之间也必有一个变量互补,结果导致任意相邻的两个方格(最小项)都有一个变量互补。卡诺图化简法就是利用了相邻最小项之间的这种互补关系来实现的。例如,图8中有两个相邻的方格填1,如果用最小项的形式写出它们的逻辑表达式则为:
F=A-BCD+A-BCD- (6)
由于它们含有互补变量D和D-,根据公式D+D-=1,可以将(6)式化简:
F=A-BCD+A-BCD-=A-BC(D+D--BC
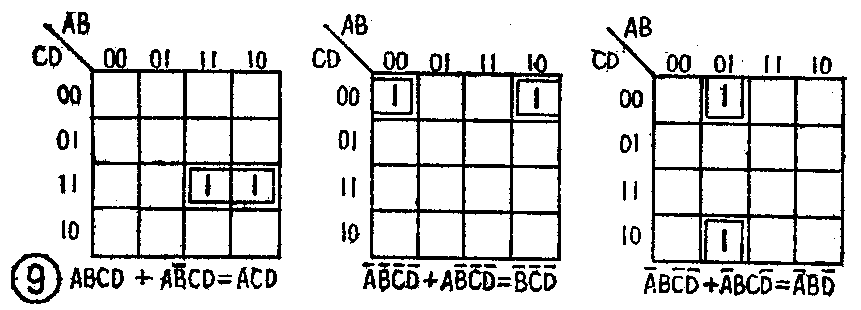
这样就消去了它们的互补变量,只留下了一个乘积项(是它们的公因子),而这个乘积项就是代表这两个方格的最简逻辑表达式。实际的作法当然不是这样一步一步地用数学式子进行推导,而是,只要见到卡诺图上有两个填1的方格是相邻的,就用小框把它们圈起来,直接写出它们的公因子。这就是在卡诺图上合并两个最小项的方法。此外,在卡诺图上,虽然上下边缘对应的方格和左右边缘对应的方格在位置上并不相邻,但由于它们也各有一个变量是互补的,因此也能够像相邻最小项一样,合并成一个乘积项,为此,我们也认为它们是相邻的。图9列举了各种相邻情况的两个最小项的合并方法。
四个和八个相邻最小项的合并步法
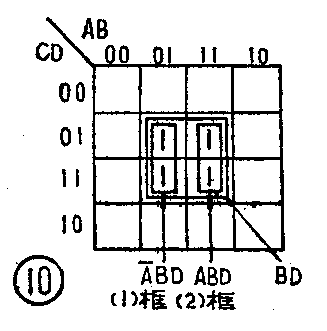
图10有四个相邻的最小项,根据两个相邻最小项的合并方法,可以先把(1)框和(2)框分头合并,然后把它们加起来,于是得逻辑表达式
F=A-BD+ABD (7)
式(7)中的两项仍含有互补变量A和A-,因此还能进一步化简:
F=A-BD+ABD=BD(A-+A)=BD
由此我们可以得出结论:凡是四个相邻的最小项也可以合并成一个乘积项,该乘积项就是四个相邻最小项的公因子。在图上合并的方法是将四个相邻最小项用一个小框圈住,直接写出它们的公因子。上下边缘、左右边缘对应的四个最小项也和相邻的四个最小项一样,可以用小框圈住加以合并。图11列举了几种四个相邻最小项的合并情况。
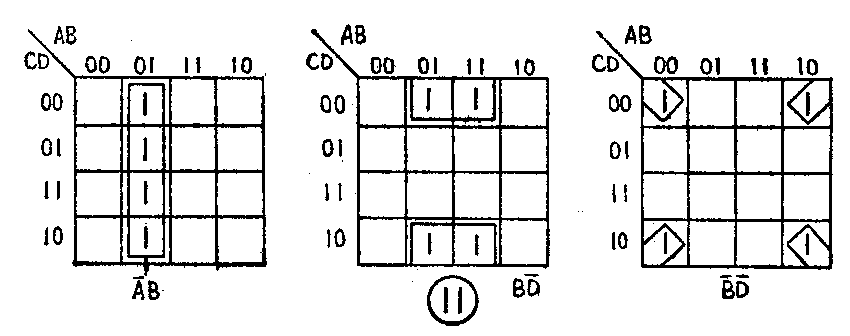
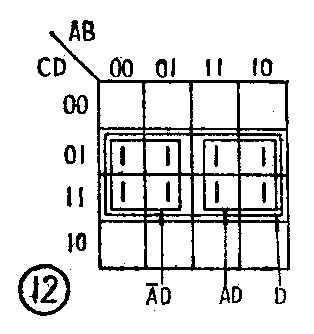
图12有八个相邻的最小项,也可以先把它分成两部分,每一部分则包含着四个相邻的最小项,分头合并后再相加得:
F=A-D+AD (8)
显然(8)式中仍含有互补变量,因此还可以进一步化简
F=A-D+AD=D(A-+A)=D
由此我们又得出结论:八个相邻的最小项也可以合并成一个乘积项,这个乘积项是八个相邻最小项的公因子。合并的方法是将八个相邻最小项用一个小框圈住,直接写出它们的公因子。上下边缘和左右边缘对应的八个最小项,也和相邻的八个最小项一样,可以用小框圈住加以合并。图13画出了这两种合并的情况。
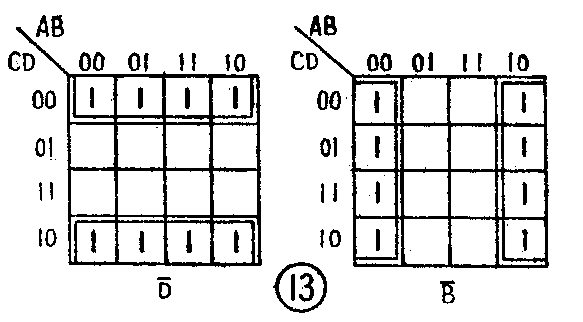
以上我们介绍了二、四、八个相邻最小项的合并方法。这里有两个问题需要注意:一是只有相邻的和上下边缘对应的最小项才能合并成为一个乘积项,而且被合并的最小项的个数必须是二、四、八等数字,其它数字,如六个相邻最小项就不能合并成为一个乘积项。二是一次圈住的相邻最小项的个数越多越好。如有四个最小项相邻,则要一次圈住四个,而不要两个一组分头去圈。
利用卡诺图化简举例
上面我们介绍了如何把逻辑表达式搬上卡诺图,也介绍了如何在卡诺图上合并最小项。这两步实际上就是利用卡诺图化简逻辑表达式的全过程。下面我们再通过几个实例,连贯地介绍一下这个过程。
例1:化简F=A-BC-+BCD-(C+D--B-CD-第一步,将逻辑表达式转换成与或形式:
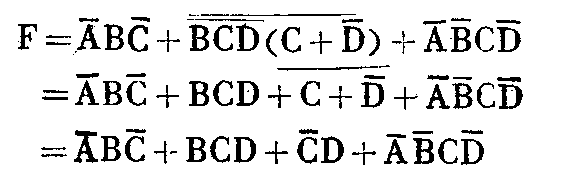
第二步,将逻辑表达式搬上卡诺图:
首先确定卡诺图的格式。上式共有四个变量A、B、C、D,因此需用四变量卡诺图的格式。其次把逻辑表达式逐项搬上卡诺图,得图14。第三步,在卡诺图上合并最小项:
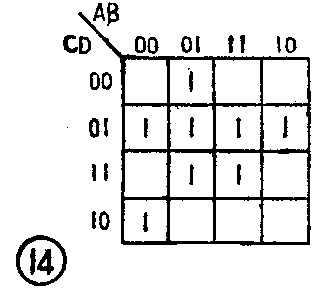
合并的方法是,从任一个填1的方格开始,寻找和它相邻的填1的方格一起圈起来,圈住的数目越多越好。再从另外填1的方格开始,重复上述过程,直到卡诺图上全部填1的方格都被圈过为止,不得漏圈。本例的合并过程参看图15。图中(1)框的公因子(即化简的结果)为C-D,(2)框的公因子为A-BC-,(3)框的公因子为BD,(4)框填1的方格是孤立的,和哪一个填1的方格都不相邻,因此,只能将它本身圈起来。第四步,把各小框的化简结果加起来,便得最简逻辑表达式:
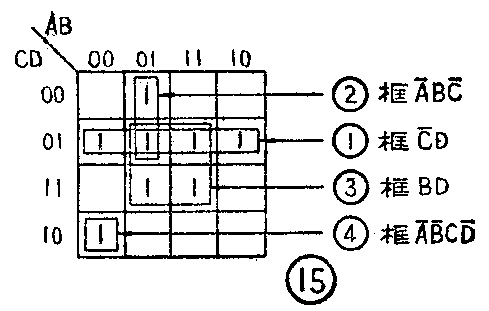
F=A-BC-+C-D+BD+A-B-CD-
例2:已知卡诺图如图16所示,求用它表示的最简逻辑表达式。
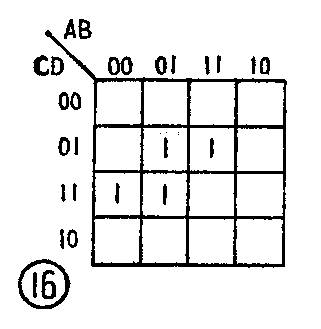
如果根据例1的步骤和方法,最后可得逻辑表达式
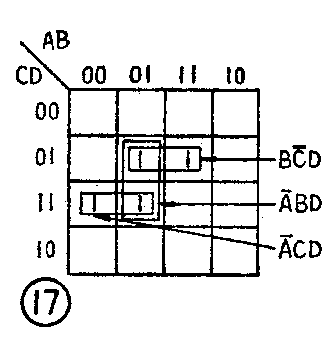
F=A-CD+A-BD+BC-D(参看图17)
然而上式并不是最简逻辑表达式,我们可将其中的公因子Dl提出来,于是得:
F=(A-C+A-B+BC-)D
括号内的A-B可应用基本公式“去第三项律”而消去,这样便得:
F=(A-C+BC-)D=A-CD+BC-D
此式才是最简逻辑表达式。
为什么会出现不是最简的情况呢?由图17可以看出,对应多余乘积项A-BD的小框圈起来的两个填1的方格都被圈过两次,而另外两个小框都至少有一个填1的方格未被圈过两次。因此,在用卡诺图化简逻辑表达式时又应注意以下两点:
一、卡诺图上所有填1的方格,都至少应被圈过一次。此点保证了逻辑表达式不会因为化简而被弄错。
二、每个圈起来的小框中,至少应保证有一个方格未被圈过两次。此点保证了所得结果为最简逻辑表达式。
至此,我们就把用卡诺图化简逻辑表达式的方法介绍完了。为了进一步说明用卡诺图化简的优越性,下面我们再举一例。
例3:化简F=AB--D+DC+BD
先用卡诺图化简法。因为上式本身就是与或式,所以可直接填写它的卡诺图,得图18。在图18上合并最小项的结果得最简式
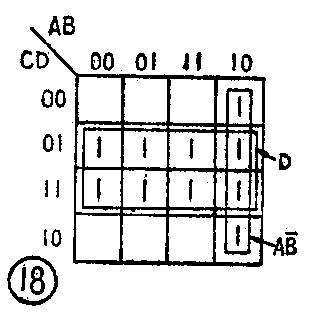
F-+D
再用公式化简法,化简过程如下:
F-+A-D+DC+BD
-+(A-+B)D+DC
--D+DC
利用公式A+A-B=A+B,-看作是一个变量,则
AB--D+DC
-+D+DC
-+D
两种方法加以比较,可以明显地看出,卡诺图化简法规律性很强,不管多么复杂的式子,只要按照规定的几个步骤去作,都能得出明确的结果。公式化简法则没有什么确定的规律性,而是需要一定的技巧。由此就可见卡诺图化简法的优点了。(杨延善)