用卡诺图化简逻辑表达式

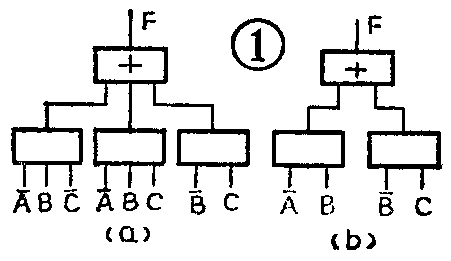
代表一定逻辑功能的逻辑表达式可以有很多个，和这些逻辑表达式相对应的逻辑电路自然也就不同，这中间会有繁简的差别。为了判断一个逻辑电路是不是已达到最简，可以先写出它的逻辑表达式，然后应用逻辑代数中的定律、规则和基本公式对它进行检查，看看是不是还能化简。如果已无法再化简，我们就认为这个逻辑电路是最简单的。例如，对于图1a的逻辑电路，可写成下列逻辑表达式：

（1）式前两项提公因子A-B后得：

因为C-＋C=1，因此上式为：

查看（2）式比（1）式简单，而且已无法再化简，因此我们便可得出结论：图1a的电路不是最简单的，而由（2）式画出的图1b电路才是最简单的。

上面说的化简逻辑表达式的方法称为“公式法”或“代数法”。这种方法在1980年第11期曾作过介绍，这里只简单地提一下。该方法的优点是过程简单，书写方便。但是，它却有很大的缺点，第一，人们必须熟记逻辑代数中的各个定律、规则和基本公式；第二，化简过程没有什么确定的规律性，基本上是使用“试探”方式；第三，最终的结果是不是最简单，也不容易看出来。这些缺点对于初学者，或不经常设计逻辑电路的人来说，更加显得突出。为了克服这些缺点，人们找到了一种规律性较强的、直观的、用图形来化简逻辑表达式的方法，这就是本文将要介绍的卡诺图化简法。

以前我们介绍过真值表。在介绍卡诺图之前，我们先把真值表的意义复习一下。为了便于说明问题，我们来考察一个只有两个变量的逻辑表达式：

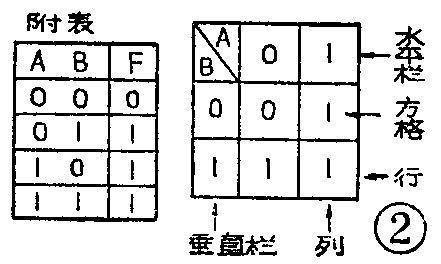
（3）式说明了什么样的逻辑功能呢？第一，只要A=1，不管B是0还是1，F都为1；第二，B=1、A=0，F也为1；第三，A=0、B=0，F便为0。如果将上述的逻辑功能列成表格，就是所谓的真值表，见附表。真值表将输入变量为各种可能的状态时所得到的输出函数的状态都列了出来，并无遗漏，因此它和逻辑表达式本质是相同的，只是形式不同，一个采用数学公式的形式，另一个则采用表格的形式。

说明了其值表与逻辑表达式的关系之后，我们再把附表的形式作一些变换，例如变成图2的形式。变换的方法是：把附表中的变量A和B分别放在图2中的水平栏和垂直栏内。例如将A放在水平栏内，由于它有两个状态（0和1），每一个状态占水平栏内的一个方格，因此共占两个方格。把B放在垂直栏内，它也只有两个状态，因此也占垂直栏内的两个方格。我们把垂直的方格串叫作列，水平的方格串叫作行。那么，在行和列交叉的方格内，正好应该是附表中F的状态。例如，当A=0、B=0时，在附表中有F=0，这个0就应填写在A=0的那一列和B=0的那一行的交叉的方格之中。显然，附表和图2的实质内容是一样的，只是表格的画法有点变动而已。附表中的F栏就是图2中的A和B交叉的方格。已经说过，附表叫作真值表，于是图2可以叫作“真值图”。由于卡诺（人名）在1953年首先提出这种真值图并利用它来化简逻辑表达式，因此一般都称真值图为“卡诺图”。

卡诺图既然是由真值表演变而来的，当然它也具有真值表的一切特征。例如，对于同一个逻辑功能来说，虽然可以有多个不同的逻辑表达式，但它们的真值表却只有一个，因而它们的卡诺图也只有一个。对于不同的逻辑功能来说，它们的真值表不同，因而它们的卡诺图也不相同。

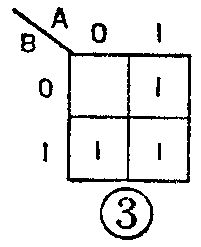
上面我们介绍了有两个变量（A和B）的卡诺图的格式。由于卡诺图的结构是人为规定的，因此在画法上并不统一，实际上，具有两个变量的卡诺图，更常见的画法如图3所示。图3是把图2中水平变量栏上方和垂直变量栏左方的外框线去掉，而且为了简便起见，在方格中只标出1，不标出0。

当逻辑表达式有三个变量或四个变量时，自然也应当有和它们相对应的三变量或四变量的卡诺图。三变量卡诺图的格式如图4所示。三个变量用字母A、B、C来表示，水平栏上放置变量A和B，垂直栏上放置变量C。由于在水平栏上的变量有两个，因此共有四种状态组合。我们规定这四种状态组合从左到右按照“00、01、11、10”的顺序放在水平栏上。垂直栏的情况和二变量卡诺图一样，从上到下按照“0、1”的顺序放置。四变量卡诺图的格式如图5所示。四个变量用字母A、B、C、D来表示，其中A和B放在水平栏上，C和D放在垂直栏上。它们的状态组合的放置顺序均为00、01、11、10。至于五变量或更多变量的卡诺图，由于过于复杂，实际工作中较少使用，因此就不再加以介绍了。

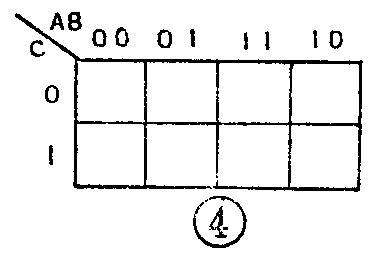
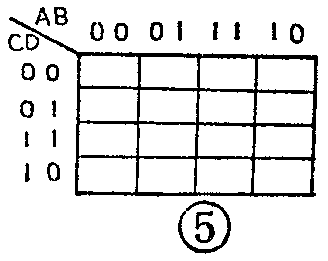
需要说明，在图4、5中，水平变量和垂直变量交叉的方格均是空的，没有填1。这是因为我们没有给出具体的逻辑表达式，所以无法知道应该在哪个方格里填1。不同的逻辑功能具有不同的逻辑表达式，因此它们所对应的填1的方格也不同。下面我们就介绍如何画出和一个逻辑表达式相对应的卡诺图，也就是如何将逻辑表达式搬上卡诺图。

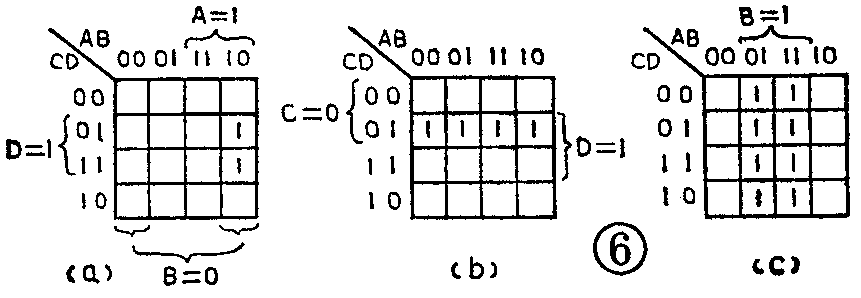
对于这个问题，当然可以仿照由附表变成图2的那种作法，先把逻辑表达式变换成真值表，再由真值表变成卡诺图。但是这种作法很麻烦。下面我们要介绍的是直接将逻辑表达式搬上卡诺图的方法。这个方法分两步进行：首先是必须弄清逻辑表达式具有几个变量（几个不同的字母），以便确定使用几变量的卡诺图格式；其次是将逻辑表达式中的每一项逐个地搬上卡诺图。例如有逻辑表式

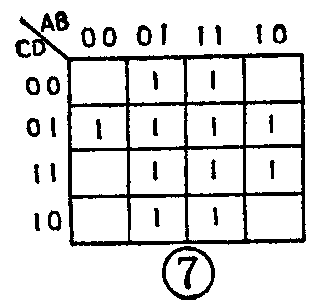
我们考察（4）式，得知它有四个变量：A、B、C、D，因此应当用四变量的卡诺图格式（图5）。可以先将（4）式中的第一项AB-D搬上图5，得图6a。这一项的意思是当A＝1、B＝0、D＝1时，函数值F便为1。察图6a中满足A=1的方格有“11”和“10”两列，满足B=0的方格有“00”和“10”两列，满足D=1的方格有“01”和“11”两行。由于AB-D中各变量相互之间是“与”的关系，因此满-D=1的方格应是同时满足A=1、B=0、D=1的方格。由图6a可以看出，同时满足这些要求的方格只有两个，因此只能在这两个方格上填1，说明这两个方格就代-D=1。按照同样的方法，把第二项C-D搬上图5，得图6b，把第三项B搬上图5，得图6c。注意图6a和图6b以及图6c中填1的方格有重迭，但这不会影响函数的值。因为AB-D、C-D和B这三项是逻辑加的关系，即使在某些方格中，它们都为1，由于1+1=1，其结果仍然为1。最后，将图6a、b、c相加，则得图7。这就是说，图7所示的卡诺图就代表着逻辑表达式

以上我们由图6一步一步地得到图7，如果熟练了，则可以直接画出图7，而省掉图6所示的中间步骤。

最后再说明一点，逻辑表达式（4）具有“与或”式的形式，也就是说，它是由几个乘积项相加而构成的，而每一个乘积项中都不出现一个非号下面覆盖两个或两个以上变量的情形。如果不是“与或”式的形式，就应该首先将它变成“与或”式的形式，然后再按上述步骤进行。例如，设逻辑表达式为

则首先应该用摩根定律将B＋A-C中的大非号去掉，得：

再将A-C中的大非号去掉，得：

最后用分配律将B-乘入（A＋C-）中，得：

这就变成了与或式的形式了。（下期续）(杨廷善)