没有立方根运算键怎样开立方？

编者按：本刊今年第三期刊登了吴波同志的“没有立方根运算键也能开立方吗？”一文以后，引起了很多读者的兴趣，纷纷来信来稿，指出探讨扩大袖珍计算器的使用范围问题很有实际意义。但是大家都认为吴波同志所提出的方法太复杂，需要动手又动笔，运算过程中容易产生差错。不少同志提出了不采用笔记的方法，只用按键就能得出答案，既简便，又不易出错。我们从中仅选出了三篇发表，其它同类文章，限于篇幅，恕不能一一刊登出来。

在我们讨论开立方的按键程序之前先作一个实验。使用只有开平方功能的算术计算器，按入27这个数字后，按动10次开平方功能键，然后按2次乘号键（有的计算器按1次就可以，按2次也无妨），接着按10次等号，然后又按2次乘号，接着再按30次等号，这时计算器的显示数就是27的立方根的近似值。各种计算器按完后的显示数可能在小数点第三位以后不完全一样，这是因为它们的运算器大小不一样的缘故，但它们和3（27的立方根）的误差都很小，如果把小数部分四舍五入，那就得3。这是用什么道理开立方的呢？下面从计算器和数学两方面来分析这个问题。

先从计算器谈起。有些算术计算器上有X\(^{2}\)这个功能键，而有些则没有。我们已经知道，没有X2功能键的计算器也能作乘方运算，办法是按动[×][×][=]键。例如按入数字a以后，接着按动[×][×][=]键，则显示a\(^{2}\)的数值。读者可用任意数字代替a，实验一下，肯定是对的。若在按动[×][×]键以后，不只是按1次[=]键，而是连续按[=]键，则是将a这个数连续自乘。按1次等号，就自乘1次得a2，按2次等号就自乘2次得a\(^{3}\)，按n次等号则得an+1。这时如果再按2次[×]键，以后按[=]键则是要将a\(^{n}\)+1这个数进行自乘，按1次[=]键得（an+1)\(^{2}\),按2次[=]键得（an+1)\(^{3}\)，按m次[=]键得（an+1)\(^{m}\)+1=a(n+1)(m+1)。根据这个原理，在求一些数的乘方时，可以大大节省按动[=]键的次数。例如，求2\(^{24}\)=？输入2并按动[×][×]键以后，本应连续按动23次[=]键。但是由于24=3×8=3×2×2×2，所以224=2\(^{3×2×2×2}\)={[(23)\(^{2}\)]2}\(^{2}\)。于是，在计算器上就可以这样按：2[×][×][=][=][×][×][=][×][×][=][×][×][=]。按完后所显示的结果就是224幂。

以上介绍了用计算器求平方和连续自乘的按键方法，下面结合一些数学分析，推导开立方的程序。

从代数方根运算法则我们知道，\(\sqrt{a}\)=\(\sqrt{4}\)\(^{a}\)=a\(\frac{1}{4}\)=a\(^{1;2}\)2,\(\sqrt{a}\)=\(\sqrt{8}\)a=a\(\frac{^{1}}{8}\)=a1;23。由此可见，在计算器上，按1次平方根功能健，即开1次平方，按2次则连续开2次平方，即开2\(^{2}\)次方，按n次，则开2n次方。如果能找出适当的n、m值，使m／2\(^{n}\)=1／3，则a1/3=a\(^{m}\)/2n。显然，a\(^{m}\)/2n=（a\(^{1}\)/2n）\(^{m}\)。a1/2\(^{n}\)就是将a开n次平方，（a1/2\(^{n}\))m就是将a开n次平方以后，再进行m次乘方。这就是用开方、乘方运算代替开立方运算的数学根据。2\(^{n}\)是这样的一系列数:2、4、8、16、32、64、128、256、512、1024、2048、4096……。既然m/2n=1/3，那么m就应当是2\(^{n}\)被3除以后所得的商数。但上述2n的一系列数都不能被3整除，只能通过四舍五入取其近似值。2\(^{n}\)的值越大，m/2n越接近1/3。例如取2\(^{n}\)=1024，则m=1024÷3=341.3≈341，于是得a1/3≈a\(^{341}\)/1024=（a1/1024）\(^{341}\)=（a1/210)\(^{341}\)。用计算器求（a1/210）\(^{341}\)时，按键次序应是先开方后乘方。因为若先乘方，计算器可能发生溢出，而溢出后就无法运算了。此外，为了减少按键操作次数，我们又把341化为11×31，因此，3a≈(a\(^{1}\)/210)\(^{341}\)=（a1/2\(^{1}\)0)11×31=[（a\(^{1}\)/210)\(^{11}\)]31的按键程序是：

从理论上讲，n和m取得越大，m／2\(^{n}\)就越接近1／3，计算出来的结果就越精确。但由于受到计算器运算系统位数的限制，n和m取得过大，精度并不会提高。一般2n取1024已经足够了。因此可以把上述程序作为开立方的固定程序来记。用熟了以后，计算起来是很方便的。

上面介绍了近似计算\(\sqrt{3}\)\(^{a}\)的按键程序，那么能不能推而广之计算一些更复杂的问题呢？回答是能！比如求6a=?可使\(\sqrt{6}\)\(^{a}\)=\(\sqrt{3}\)a≈a\(^{341}\)/2048=[(a1/2\(^{11}\))11]\(^{31}\)，这个式子和3a比较，只是开平方的次数比\(\sqrt{3}\)\(^{a}\)多1次，这就是说只要在按[倍喟1次就可以了。又如，求6a\(^{5}\)的值时，可使\(\sqrt{6}\)a\(^{5}\)=(\(\sqrt{3}\)a)\(^{5}\)≈(a1/2\(^{11}\))11×31×5，按键程序是：

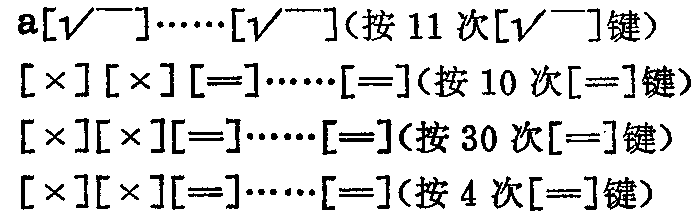
以此类推，可以求出一个数的任意次开方。（董健廉）

下面我介绍一种不用手记而开立方的简便方法。我们用数学方法把13表达成下列无穷乘积：

取前面若干项的乘积，它们的值都是\(\frac{1}{3}\)的不同精度的近似值。例如：

我们可以看到，取的项数越多，其乘积就越接近\(\frac{1}{3}\)。事实上，只要取四～五项就足够准确了。在这个基础上，就可以推导出计算\(\sqrt{3}\)\(^{a}\)=a1/3的近似公式：

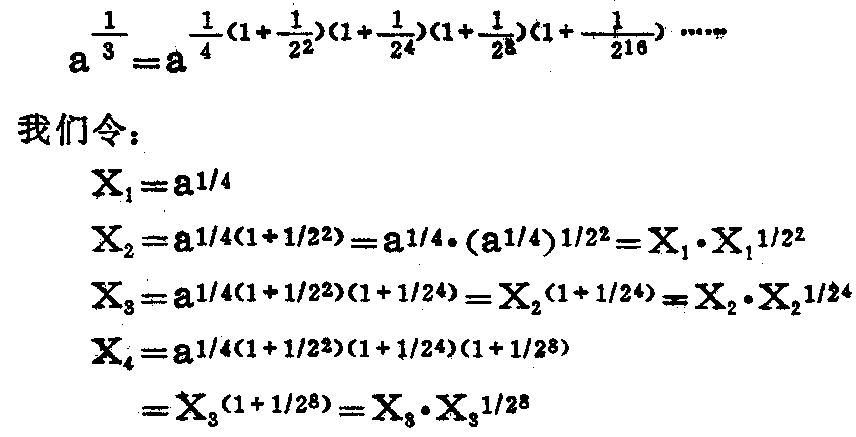
由上面的推导，可以得出这样的结论：如果已计算出\(\sqrt{3}\)\(^{a}\)的一个近似值X\(_{n}\)，那么按下列公式就可算出另一个准确度更高的近似值Xn＋1。该公式为：X\(_{n＋1}\)＝Xn·X\(_{n}\)（1/2）2\(^{n}\)，而Xn（1／2）\(^{2}\)n就是将X\(_{n}\)连续2\(^{n}\)次开平方，这在计算器上操作是很方便的。这样我们就可以很容易地得到如下的按算方法：

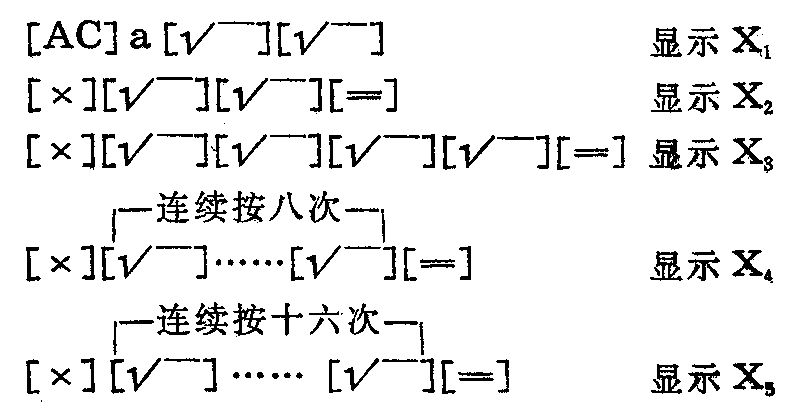
上述按键程序是有规律的：显示X\(_{2}\)以后，每再按一次[×]键，则[陌炊问驮黾右槐丁Ｕ飧龇椒虻ヒ准恰⒍冶阌谠谑褂弥邪淳纫笕≈怠＠1：求\(\sqrt{3}\)\(^{27}\)=？

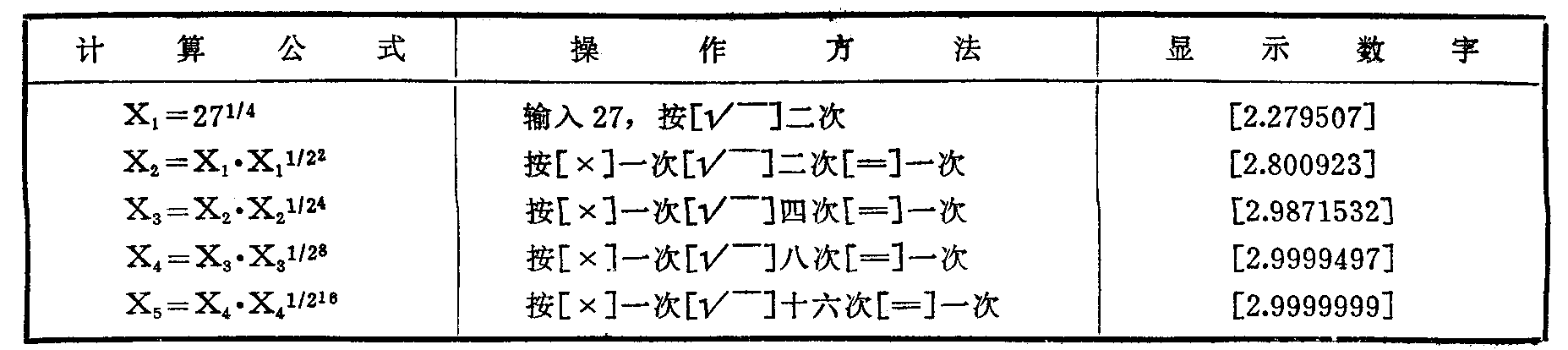
如何掌握运算精度呢？我们认为，当1＜a＜1000时，取到X\(_{4}\)或X5，一般就能满足运算精度的要求了。至于大于1000（或小于1）的正数，可以先把它缩小（或扩大）10\(^{3}\)\(_{n}\)倍，使它转换成1000与1之间的数，求出该数的立方根后，再扩大（或缩小）10n倍。

先按上述方法求出\(\sqrt{3}\)\(^{27}\)≈2.9999999，于是得

如果a是负数，则先把它的绝对值开立方，然后再加上“-”号即可以了。

将上述方法推广一下，还可以得到求\(\sqrt{5}\)\(^{a}\)的近似公式。

读者可参考前述方法找出求\(\sqrt{5}\)\(^{a}\)的按键程序。（杨声）

我这里提供用[⒎降挠忠环椒āＲ阎桓鍪齛，要求开立方。我们先假设a的立方根为X，则X\(^{3}\)=a。将此式两边各乘以X,则得X4=aX,于是X=\(\sqrt{4}\)\(^{aX}\)。这样我们就把开立方的问题化为开四次方的问题了。我们知道，用计算器开四次方，就是连续两次按动[Ｉ鲜街校琣是给出的数，X是待求的数。因为等式两边都有X,我们又不知道X是多大，所以也就无法求出aX的具体值，当然也就不能用连续按两次[姆椒ń玜X开四次方。怎么办呢？我们可以先假设4aX中的X为一确定的数X\(_{0}\)（这个数和真正的X值不会相等，因为是随意假设的，不是求出来的），于是就可以求出\(\sqrt{4}\)\(^{aX}\)0的值了。方法是将a与X\(_{0}\)相乘，再连续按两次[Ｎ颐橇頧1=4aX\(_{0}\)。因为X1是用a和假设的X\(_{0}\)两者求出来的，包含了正确的成分，所以X1一定比X\(_{0}\)接近于我们所要求的X值。试举一例，求\(\sqrt{3}\)\(^{8}\)=？根据X1=4aX\(_{0}\)可得X1=\(\sqrt{4}\)\(^{8X}\)\(_{0}\)。随意假设X0＝1，则X\(_{1}\)＝48×1=1.6817928，可见X1比X\(_{0}\)接近于\(\sqrt{3}\)\(^{8}\)=2。利用求出的X1值，还可再求X\(_{2}\)=4aX1,求出的X\(_{2}\)又一定又比X1接近于真正的X值。如上例中令X\(_{2}\)=\(\sqrt{4}\)\(^{8X}\)1=48×1.6817928=1.9152065，可见X\(_{2}\)更接近于2。以此类推，还可求出X3=\(\sqrt{4}\)\(^{aX}\)\(_{2}\)，X4=4aX\(_{3}\)，……Xn=\(\sqrt{4}\)\(^{aX}\)\(_{n}\)-1。实际上，这是一个无限次的数学逼近的过程，只要n取得足能大，求出的Xn与真正的X值误差就会很小，可以忽略不计。

前边谈到，X\(_{0}\)可以随意假设，不管X0和真正的X值相差多大，一步步求下去，总能逼近所要求的X值。只是两者相差较大时，求的次数要多一些。为简单起见，我们就固定地取X\(_{0}\)=1，于是得：

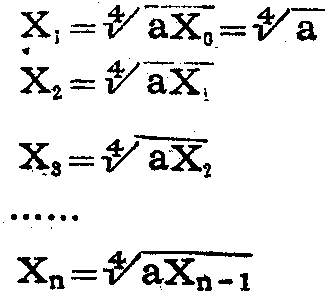
由此我们不难导出求立方根的按键程序：

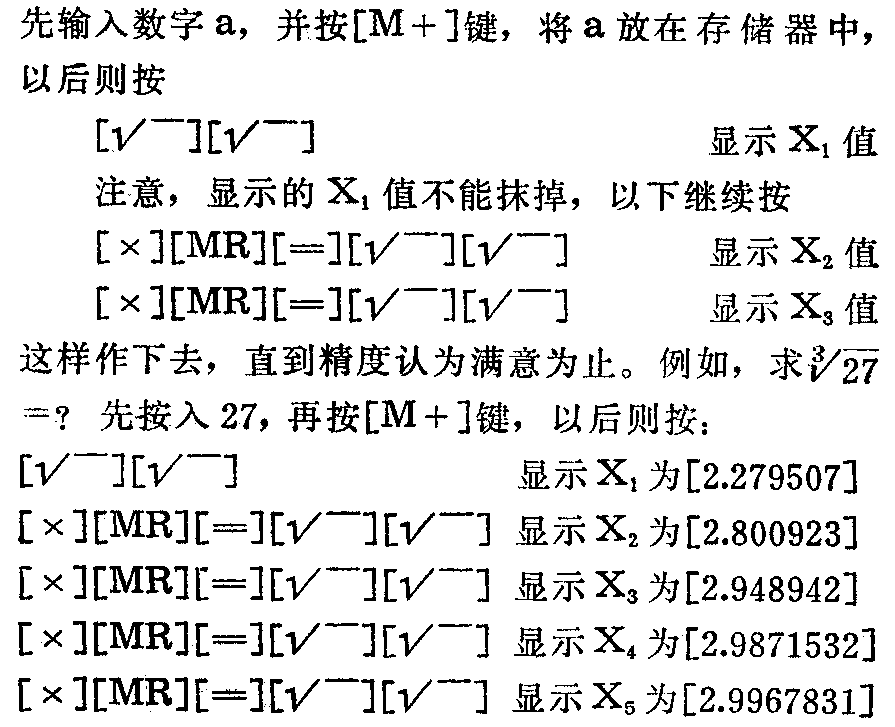
我们知道，27的立方根是3，这里按了五次以后显示的数X\(_{5}\)已经很接近于3，如果认为精度还不够高，可以再继续按下去。但是，由于计算器字长（八位）的限制，像上面的例题，当n=13时，X13=2.9999999，再运算下去还是这个数，精度不会再提高了。

利用同样的推导方式，可以找出开五、六、七……次方的按键程序。下面以开五次方为例，加以说明。

设开数a的五次方。令\(\sqrt{5}\)\(^{a}\)=X, 则X5=a。两边各乘以X\(^{3}\)，得X8=aX\(^{3}\)，X=8aX\(^{3}\)。又令X\(_{1}\)=\(\sqrt{8}\)aX\(^{3}\)0，取X\(_{0}\)=1，则X1=8a, X\(_{2}\)=\(\sqrt{8}\)\(^{aX}\)31,X\(_{3}\)=\(^{8}\)aX32……X\(_{n}\)=\(\sqrt{8}\)\(^{aX}\)3n-1。

取a为32，则按键程序为:

读者可根据以上方法推导开任意次方的按键程序。（徐丹峰）