我们知道,逻辑代数中每个逻辑表达式所表示的逻辑功能都可以用相应的逻辑电路来实现,逻辑表达式和逻辑电路是一致的。有经验的人,看到一个逻辑表达式,就能立即画出它的逻辑电路图;反之,看到一个逻辑电路图,也能很快地列出它的逻辑表达式。这是两种最基本的技能,学习逻辑电路知识必须首先要掌握它。
怎样画图和怎样列式
下面我们就谈谈已知逻辑表达式怎样画出它的逻辑电路图,而已知逻辑电路图,又怎样列出它的逻辑表达式。
假定有一个逻辑表达式为P=AB+B--,要求画出它的逻辑电路图。我们看到这个式子大非号下第一项AB是“与”的关系,可用一个两输入端与门来实现;第二项B-是把B取反,可用一非门来实现;这两项之间又是“或”的关系,因此应该把与门和非门的输出分别送到一个或门的两输入端。因为整个式子还有一个“非”号,表示要整个地取反一次,所以上述或门的输出还要加接一个非门。这样,按左边是输入,右边是输出的规定,就可画出逻辑电路图1a。最后再整理一下,把输出端的或门和非门合并成或非门而得到图1b。这就是逻辑式P=AB+B-的逻辑电路图。
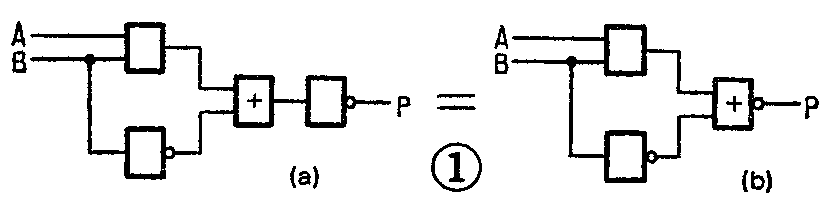
从逻辑式画出逻辑电路图的方法大致是:
(1)弄清楚每一项以及项与项之间的逻辑关系,用相应的逻辑框图代替;
(2)接从左到右的顺序逐项画出逻辑框图,最后得出全式的逻辑图。也可以在每个框图的输出端写上它们的逻辑关系式,这样看起来更清楚。
(3)最后再进行整理,得到完整和清晰的逻辑电路图。
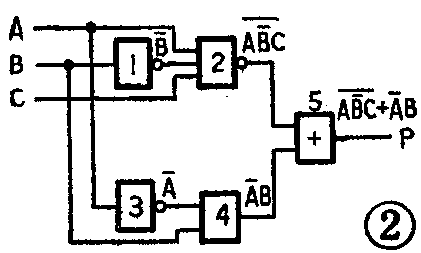
下面我们再结合图2,看看怎样列出一个逻辑电路的逻辑表达式。我们可以先把这些门按从左到右的顺序编上号,然后再从左边输入端开始,一一地写出每个门的输入和输出间的逻辑关系。图2中门1的输出是B-,门2-C,门3是A-,门4是A-B,最后门5的输出,也就是整个电路的逻辑表达式为
P=AB-C+A-B
与门和或门的变换
在对逻辑问题进行电路设计时,一般都是先列出逻辑表达式,然后再用相应的逻辑电路来实现它。但是,在搞技术革新时,实现逻辑表达式所要求的元器件和我们手头上已有的不一定相符。例如,电路中需要或门,而手头上只有与非门,这时就需要将逻辑表达式进行变换。
以前我们讲过摩根定理,其中等式
A+B--B-
的左边是一个或非门(图3a),右边是两个非门进行逻辑乘(图3b)。另一个等式
AB---
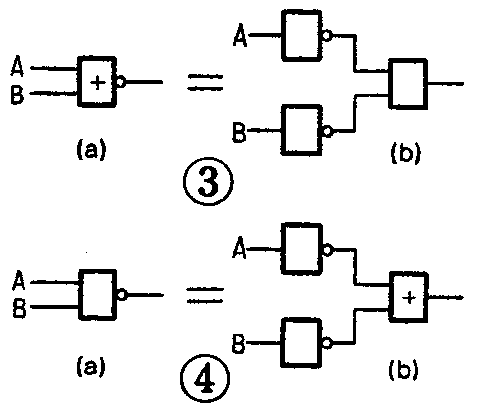
的左边是一个与非门(图4a),右边是两个非门进行逻辑加(图4b)。
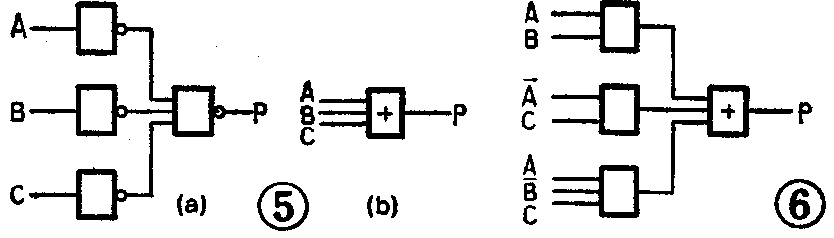
从这两个式子我们可以看到,与门和或门是可以互相转换的,就是说,在不改变逻辑功能的前提下,可以把与门交换成适当形式的或门,也可以把或门变成适当形式的与门。例如用这种方法可以很方便地把图5a变换成图5b。它们的逻辑式为A-B-C-=A+B+C。图5a是与非门,图5b是或门。又如,以前介绍过的异或门,其逻辑表达式为P=AB--B。用电路实现它,既需要与门,又需要或门。如果用摩根定理进行变换,则

最后的式子只需要与非门一个品种。
利用摩根定理进行与门和或门的变换,在逻辑设计中是经常会遇到的,这个方法不但要学会,而且要记熟。
逻辑表达式的公式化简法
由设计直接得到的逻辑表达式往往很繁杂,对这样的表达式,除了根据已有的材料进行适当交换以外,在大多数情况下,都需要化简。这里自然会提出一个问题,就是对于不同类型的表达式来说,怎样才算是“最简”?
在实际应用中,一般都以与或式作为标准表达式,然后给它以“最简”的标准。因为,第一,原始设计得到的表达式多为与或式;第二,与或式和其它类型的表达式互换较简单。一般我们把与或式中的与门数叫作项数,与门输入端数(包括重复的)叫作变量。例如图6所对应的逻辑表达式P=AB+A-C-C共有3个与门(3项),7个输入端(包括重复的共7个变量)。因此,与或式的最简标准应是:首先项数必须最少;其次,在项数最少的条件下,变量数也最少。
化简逻辑表达式有多种方法,现在介绍利用逻辑代数的基本公式进行化简的方法,通常有下列三种:(为便于理解,附表中列出了一些常用的公式供参考)
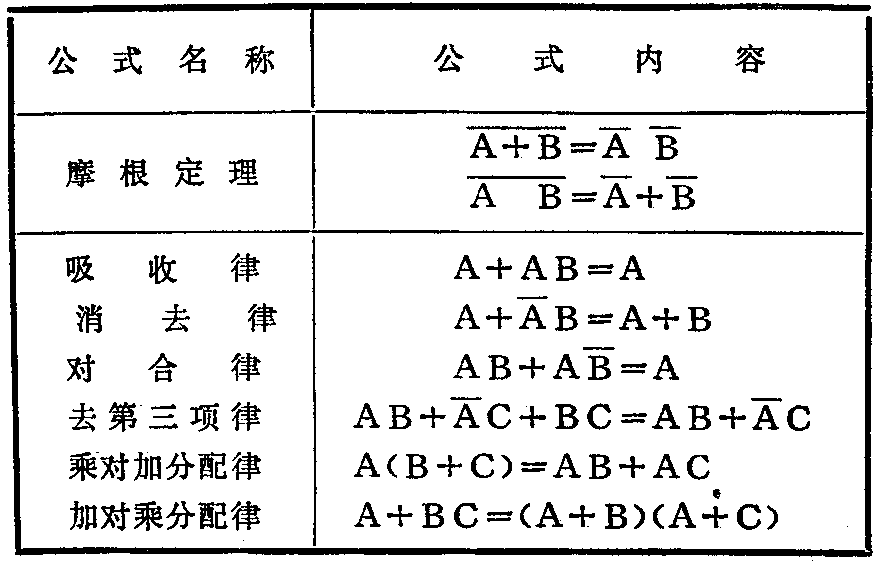
(1)合并法 利用基本公式把两项合并成一项,并在合并过程中消去一个变量。
例1: P=AC+AC-
=A(C+C-)=A(∵C+C-=1)
可以将本式看成是一个常用公式,用文字说明则为:两与项有公共因子,且余下的部分又互补(相反)时,则此二项可用公共因子代之。
例2:P-C-C
=A(B-C+B-C
本例把整个B-C看成是一个因子。
(2)消去法 利用公式A+AB=A及A+A-B=A+B消去多余的项和多余的因子。
例3:P=AB--BC
=A---BC(用摩根定理)
=A--(∵A--BC=A-)
例4:P=AB+A-C+B-C
=AB+(A--)C
=AB+AB-C(用摩根定理)
=AB+C(把AB看成是一个因子)
(3)配项法 在不影响表达式逻辑功能的情况下,加上一项,或给某项乘一因子,然后再用合并法或消去法化简。
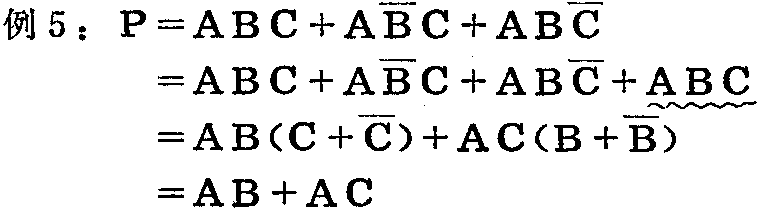
本例根据公式A+A=A,在式中增加一项ABC,然后再用合并法化简。
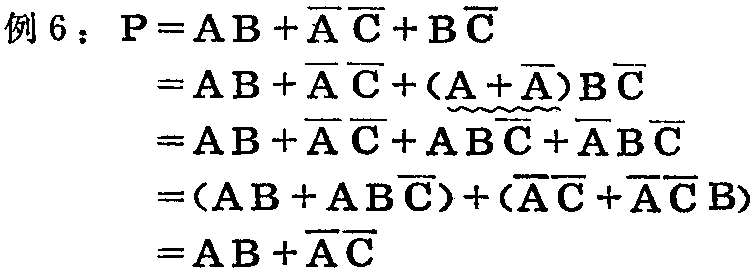
本例是在BC-项上乘以因子(A+A-)。
在公式化简法中,也可以把本式当作一个常用公式来使用。用文字说明则为:与或式中,两个与项之一包含了原变量A,另一项包含了反变量A,而且此两项的其余因子都是第三个与项的因子,则第三个与项是多余的,可取消。
实际上,化简一个逻辑表达式可能同时要用到合并法、消去法和配项法等等,只要运用得巧妙,就可以把一个复杂的式子变得很简单。但是,公式法化简逻辑表达式规律性不强,往往要经过几次试探。如对于例6,初学者就很难想到要乘一个因子(A+A-)。为便于初学者较好地掌握它,现归纳几点原则供参考。
(1)要熟记逻辑代数的各个基本公式,尤其是那些和普通代数在形式上毫无共同之处而又不直观的公式,更应熟记。
(2)一般来说,应先通过摩根定理和分配律,将待化简的表达式变换成与或式,然后再观察表达式是否有满足附表中所列的吸收律、消去律、对合律等情况,最后尚需试探用摩根定理和分配律变换表达式中的局部因子或某几项,再观察是否满足吸收律等。
(3)逻辑表达式中有时几个变量可以看成是一个变量(如例2中的B-C),这样再用基本公式进行变换就方便了。
总之,如待化简的表达式较简单,采用公式法化简是很方便的,但是,当表达式较复杂时,往往难以获得最简式,这就需要采用即将介绍的“卡诺图”法了。(方波)