怎样使用函数型袖珍电子计算器

函数型袖珍电子计算器除具备一般型计算器的运算功能（详见本刊1979年第9期）以外，还可进行三角函数、反三角函数、双曲函数、反双曲函数、对数函数、幂函数、阶乘等运算，并能进行角度换算和统计计算等等。尽管各种函数型计算器的功能有些区别，但同一功能键的操作过程却是类似的。我们以八位液晶式CASIOfX—2200型计算器（见图1）为例，简要介绍它的使用方法，供广大爱好者参考。

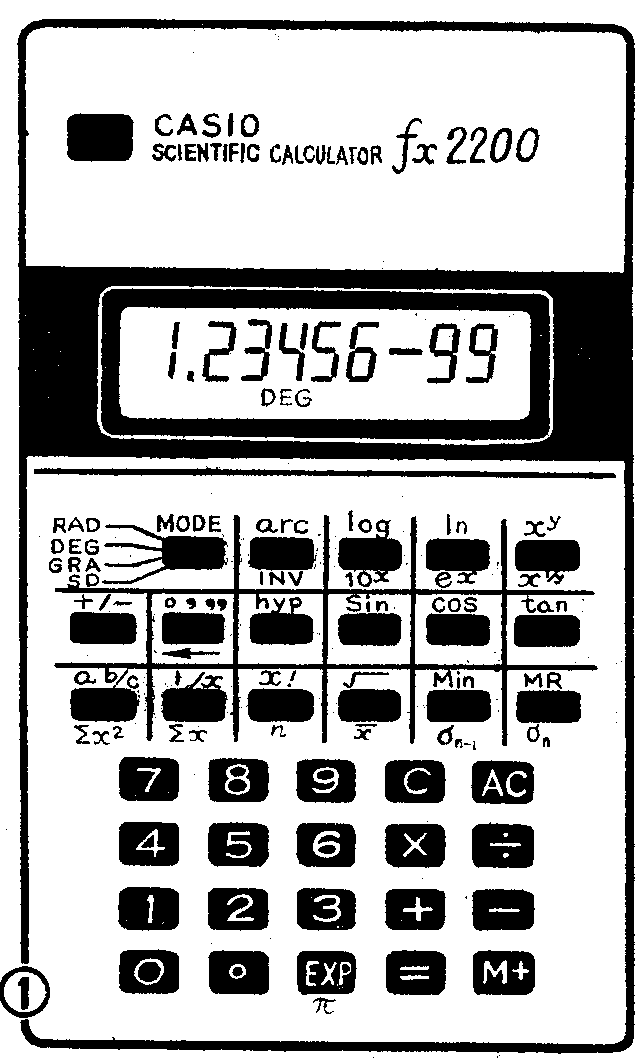
图1中显示屏上方的黑色键是电源开关。其余的键均在显示屏下方，其中数字键及一般功能键如[+]、[-]等键的标注与作用和一般型计算器相同，本刊1979年第9期已有介绍，这里不再赘述。以下就图1中未曾介绍过的按键予以说明。

［MODE］角度模式键或称度——弧度——公制度模式选择键。角的国际度量制有三种，即“度、分、秒制”（用DEG表示）、“弧度制”（用RAD表示，1弧度=180°／π≈57°17′54″）、“公制度制”（用GRA表示，这是欧洲目前正在使用的一种新的分度制，100GRA=90°=π／2弧度）。因此，在进行三角函数或反三角函数运算前，应根据角度的不同单位制，先选好相应的角度模式键，然后才能计算。选择的方法是连续按动［MODE］键，显示屏将依次显示“DEG”、“RAD”、“GRA”字样，表明选择的是哪一种单位制。

此外，在连续按动此键时，显示屏还会出现“SD”字样，这是用作统计计算的标志，详见后述。

［EXP/π］输入阶码（指数置数）与π共用键。在科学实验或工程计算中，经常以A×10\(^{n}\)的指数形式来表达一个数，称为一个数的科学表示法。其中A叫作“尾数”，n叫作“阶码”。进行这一类数的运算时，按此键后即可输入阶码数。例如输入-1.2345×10－99，则需依次按动1.2345［+/-］［EXP］99［+/-］键，计算器的显示见图2。

一个数以上述科学表示法显示时，均以显示屏的最后两位表示阶码。阶码有正负符号，该符号也占一位，正号时符号位空位，没有显示，负号时则显示“-”号。因此阶码的范围是±99，代表10\(^{±99}\)。由于阶码占了显示的位数，尾数的位数就得比八位少，尾数为正时，最大为六位；尾数为负时，最大为五位。

另外，该键是一个双重功能键，除有上述功能外，还兼作兀输入用。凡按动数字键以后再按动此键，表明该数要用科学表示法来显示，而不是输入π值；如果开机后首先按动此键，或在按动各种功能键如［+］、［-］、［×］、［÷］、［=］键以后，再按动此键，则输入π值。

［sin］［cos］［tan］三角函数键。求一角度的三角函数时，应先选好相应的角度模式，再输入角度数，最后按动三角函数键，即可显示出函数值。例如求sin30°=？先按［MODE］，至显示屏出现“DEG”，再依次按30［sin］等键，则显示函数值0.5。

［hyp］双曲函数键。在按［sin］、［cos］、［tan］键之前，先按［hyp］键，可计算出双曲函数值sinh、cosh、tanh。如求sinh3.6=？则按3.6［hyp］［sin］等键后，即显示结果18.2855。

［arc/INV］反三角函数与反函数共用键。按三角函数键之前，若按此键，可求反三角函数值，但同样要注意事先选定角度模式。如求sin\(^{－1}\)0.5=？若选“DEG”，按动.5［arc］［sin］等键，则显示30，即30°。

进行反双曲函数运算时，也按此键，操作步骤与反三角函数相似，只需多按一次［hyp］键。

该键还用作其它反函数的运算。由于［log／10\(^{x}\)］、［ln／ex］、［X\(^{y}\)／X1/y］与［°′″/←］都是双重功能键，为了区别按动同一键时的不同功能，当进行10\(^{x}\)、ex、X\(^{1}\)/y运算和角度换算时，应先按此键。其操作如下述。

［log／10\(^{X}\)］常用对数与常用反对数共用键。求一个数的常用对数（即以10为底的对数）时，输入该数字后按动此键，即显示对数值。求10X（已知X求10\(^{X}\)）时，则需先将X输入，再依次按动［INV］与此键。

［ln／e\(^{X}\)］自然对数与自然反对数共用键。求以e（=2.7182818）为底的数的对数时，需按此键。求eX时，输入X值后则需顺序按动［INV］键与此键。

［X\(^{y}\)／X1/y］两种幂函数的共用键。已知X和Y的值，求X\(^{y}\)时，依次按X［Xy］Y［=］键，即可得出结果。已知X和Y的值，求X\(^{1}\)/y时，依次按X［INV］［X1/y］Y［=］键，即可得出结果。

［°′″/←］度、分、秒（60进制）与十进制度数换算键。由度、分、秒转换为十进制度数时，需按此键。如14°25′36″=14.426666°，则按14［°′″］25［°′″］36［′″］后即显示14.426666°。若由十进制度数转换为度、分、秒时，应在输入度数后先按［INV］键，再按此键。如12.3456°=12°20′44″，则按12.3456［INV］［←］后显示［12\(^{0}\)4］，其中数字右上方的明为六十进制的度、分、秒。

［a\(\frac{b}{c}\)/∑X\(^{2}\)］分数与平方和共用键。输入分数时按此键，如输入2／5按2［ab;c］5［a\(\frac{b}{c}\)］，显示［2荩挥秩78;9，则按7［a\(\frac{b}{c}\)］8［ab;c］9［a\(\frac{b}{c}\)］，显示［769荨Ｏ允镜谋曛荆代表是分数。若需将分数化为小数，应再按［=］［ab;c］键（见分数运算实例）。

在统计计算时（按［MODE］键显示“SD”工作方式），按此键后可直接求出统计数据的平方和（见后）。

［1／X／∑X］倒数与总和共用键。输入一数字后按此键，可求出该数的倒数值。统计计算时按此键，可求出统计数据的总和（见后）。

［X！/n］阶乘与统计数据数目共用键。按数字键后再按此键，可求出其阶乘值，如求7！（=1×2×3……×7），只需按7［X！］键即显示5040。统计计算时按此键可显示已输入的数据个数（见后）。

［-］平方根与平均值共用键。输入数字后按此键，即得该数的平方根值。统计计算时，按此键可求出输入数据的平均值（见后）。

［Min／σ\(_{n－1}\)］存储输入与抽样标准离差共用键。一般运算时按此键，可将显示的数值输入存储器。在运算过程中，可以随时按［MR］键，将已存数读出，而已存数在存储器中并不消失、只有再按［Min］键存入新数时，原存数才自动清除。以前介绍过的［M＋］键，每存入新数时，都和原存数叠加，这是［Min］与［M+］的重要区别。统计计算时按此键，可求出抽样标准离差σn－1（见后）。

［MR／σ\(_{n}\)］存储读出与总体标准离差共用键。读出存储数据时按动此键；统计计算时，按此键后可求得总体标准离差值σn（见后）。

以上是f\(_{x}\)—2200型计算器的各种功能键的标注与作用。下面我们将通过运算实例进一步熟悉该计算器的使用方法。

函数型计算器都包括一般型计算器的功能，因此一般运算都能进行，而且优越性更大。CASIOf\(_{x}\)—2200型计算器在进行一般运算前，应先按动［MODE］键，使其显示RAD、DEG、GRA中的任何一种都可以，但不能显示SD。SD是统计计算的标志。

四则运算：

操作：［AC］12［+］3［＝］［×］89［÷］7［=］结果显示［190.71428］，显示的方式与一般型计算器相同。

操作： ［AC］12369［×］7532［×］74103［=］显示为［6.90368 12］。注意显示结果采用了科学表示法，这是函数型计算器的优越之处，此例若用一般型计算器计算（不能用科学表示法显示）由于得数超过所能显示的位数将出现“溢出”。

操作：［AC］1.23［÷］56［÷］78.9［=］显示为［2.78381-04］，答案仍采用科学表示法。如使用一般型计算器（八位式）则仅能显示［0.0002783］，精确度就降低了。

操作：［AC］7.9［EXP］56［÷］4.6［EXP］74［×］1.3［EXP］23［=］，显示［223260.86］。本答案又以数的一般形式来表达，因为若用科学表示法，由于位数的限制也会降低精确度。足见，该计算器能根据计算结果恰当地选取数的表达形式，以便使显示的结果尽量精确，非常巧妙。

定数运算：该机也能作定数运算，现举两例说明其操作步骤与特点。

由例2可见，被除数（或被减数）为定数时，利用附加存储器来运算则较便利。

混合运算：

结果显示［-720］。

第一次按［Min］键是存入（2＋8）的计算结果10，第二次按［Min］键是重新存入（9＋3）×10的计算结果120，而原存数10自动清除。按［M＋］是将显示数120再与存储数相加。

分数运算：

三角函数运算：

反三角函数运算：

双曲函数运算：

显示［4.48169］。

在计算sinh1.5时，按［Min］键先将1.5存入存储器，为的是计算cosh1.5时，只按一次［MR］键即可，而不必再按［1］［·］［5］三个键。

反双曲函数运算：

对数logx、lnx运算：

指数10\(^{x}\)、ex运算：

幂X\(^{y}\)与方根X1/y运算：

注意此例的输入顺序与（1）、（2）例不同，并连续按两次［X\(^{y}\)］键，这是定数幂运算的操作步骤所要求的。

倒数1／X与阶乘X！运算：

本例题采用了定数除法的操作步骤，即按动两次［÷］键，随之输入的数便成为被除数，从而使运算更加简便。足见计算器的操作步骤并不是一成不变的，可根据每一题目的具体情况灵活掌握。

在生产、管理以及科学实验中，常常需要对一些数据进行整理、分析，从而找出它们的内在规律性，这就要用统计计算的方法。在统计计算中，一些统计量（即通过观测数据计算得出的一些数量特征，是观测数据的函数）的计算是比较麻烦的。然而，利用函数型计算器进行计算则很方便。函数型计算器一般能迅速地求出统计数据的平均值X-、个数n、总和∑X，平方和∑X\(^{2}\)、总体标准离差σ\(_{n}\)、抽样标准离差σn-1等六个统计量，以便用于定量分析。这六个统计量中的前四个（X-、n、∑X、∑X2）意义比较明确，不再解释。下面简单介绍一下σ\(_{n}\)、σn-1的意义。举例来说，甲、乙两射手打靶，他们各射击三发子弹，甲命中9、7、2环，乙命中6、6、6环，显然，他们的射击次数n都是3，总环数都是18，平均环数都是6。这是否能说明两人的射击本领相同呢？对于这个问题，我们一看就能得出明确的结论：乙射手的本领要比甲射手高明。因为甲三次击中的环数分散性很大，其中一次击中9环就带有偶然性。乙虽未击中在靶心（10环）附近，然而三次击中的环数相同，说明乙的技术水平稳定，假如调整一下准星，乙射手很可能还会把成绩提高。对于这样简单的问题，我们能进行直观分析。但是对于复杂的问题，例如在科学实验中记录的几十个、几百个观测数据，就无法进行直观分析了，这时就可利用标准离差公式进行计算。在上例中，甲的σ\(_{n}\)=2.9439202，乙的σn=0，甲的σ\(_{n}\)＞乙的σn，σ\(_{n}\)越大，说明分散程度越大。所以不管多么复杂的数据，都可以通过计算σn来了解它们的特征。

σ\(_{n}\)和σn-1都是说明一组数据的分散程度的，其中：

利用计算器计算这些统计量时，应首先按［MODE］键，至显示屏出现“SD”字样，便是处于统计计算的工作方式了。

例：根据下面一组实验数据计算X-、n、∑X、∑X\(^{2}\)、σ\(_{n}\)、σn-1：

55、54、51、55、53、53、54、52

以上我们简要介绍了f\(_{X}\)—2200型袖珍电子计算器的功能和基本操作方法。由这个介绍可知，函数型计算器能够快速地完成科学实验和工程设计中很多复杂的应用计算，为我们的学习和工作带来很大的方便。不同类型的计算器的功能和操作方法都有些区别，但是只要熟练地掌握了一种计算器的操作方法，对于其它类型的计算器，经过仔细琢磨，也是不难掌握的。（陈亚东）