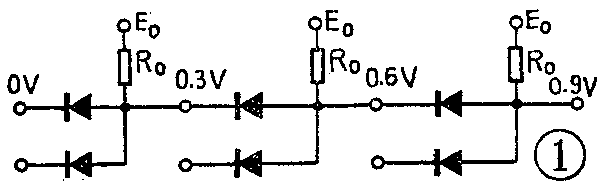
上一篇(今年第6期22页)我们介绍基本逻辑门电路时,为了突出讲逻辑关系这个主要问题,忽略了较小的二极管正向压降的影响。实际上锗二极管有0.3伏左右的压降,硅二极管有0.6伏左右的压降。在许多基本逻辑门电路互相联接的时候,二极管压降的影响就不能再忽略了。如图1所示,当第一级输入信号为0伏时,经过第一个“与”门之后就变成了0.3伏,经过两个就成了0.6伏,经过三个就成了0.9伏,这就严重地偏离了原来的数值,以致使逻辑关系发生变化而造成错误。因为存在着这样的问题,加上其它一些原因,与门和或门实际上很少单独使用,而往往是利用反相器(非门)具有的放大、整形作用,把反相器和与门、或门组合成“与非”门、“与或非”门来使用。“与非”门、“与或非”门的输出电平都由非门决定,非门只有导通和截止两种状态,即使几级串联,信号电平也不累加,因此不会过多地偏离标准数值,也就不会使逻辑关系发生错误。这种由基本门电路组合而成的电路就叫作复合门电路。复合门电路可以用分立元件组成,也可以作成集成电路,它们的逻辑功能是一样的。下面介绍几种最常用的复合门电路。
与非门
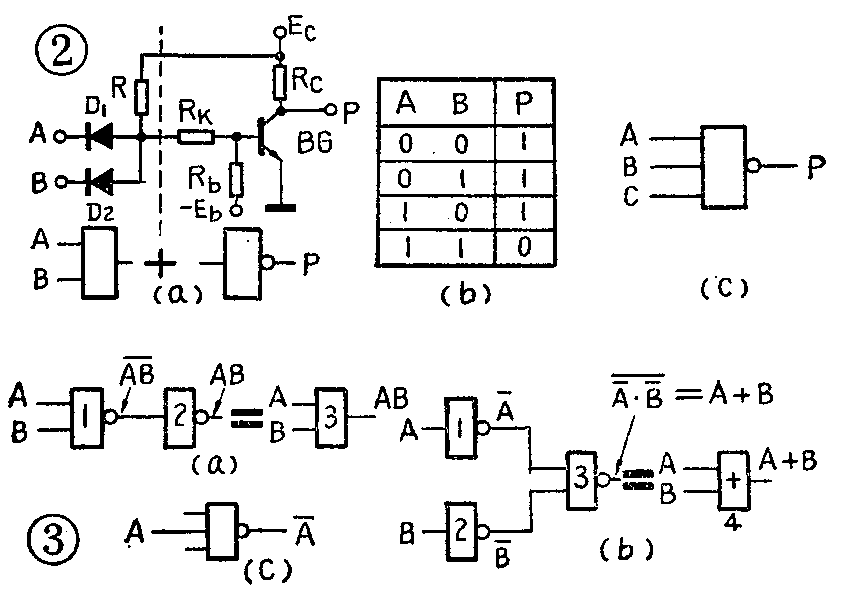
在一个与门后面接一个非门便构成“与非”门电路(图2a)。从图看到,与门的输出经反相后成为整个与非门的输出。它的逻辑功能是:输入端全为1时,输出为0;只要输入端中有一个为0,输出则为1。“与非”门的逻辑表达式为P=A·B-,它的真值表见图2b,逻辑符号见图2c。
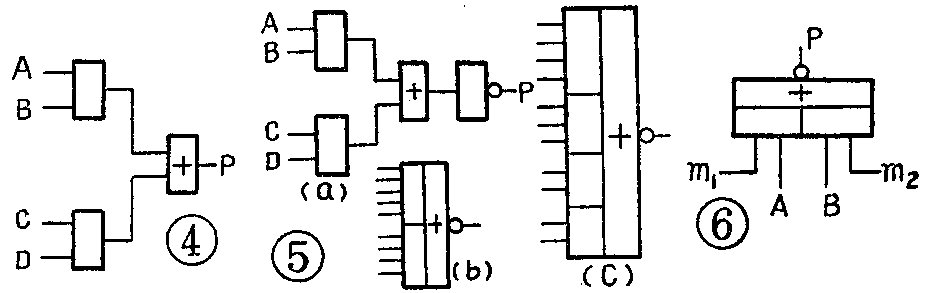
与非门能组合成与门、或门和非门,即与非门能够实现上述三种基本逻辑门电路的功能。在图3a中,与非门1和与非门2串联相当于与门3;图3b中,与非门1、2、3的联接方式相当于或门4(图中式子运算请参看今年第4期25页);图3c中,与非门的一个输入端用来输入信号,其余输入端悬空或接固定的1电平,那么该与非门就是非门。
由上述分析可以看出,使用单一品种的与非门,可以构成各种复杂的数字逻辑电路系统,而器件品种单一,给备件、调测等都会带来很大方便。这就是为什么在集成电路工业产品中,并没有与门,也没有或门,而厂家只供应与非门的缘故。
与或非门
把两个(或两个以上)与门输出端分别接到一个或门的各个输入端,便构成一个“与或”门,见图4。该图所表示的“与或”门的逻辑表达式为:P=AB+CD,而其逻辑功能则为:任何一组与门的输入端全为“1”时,输出P则为“1”;两组与门中至少都有一输入端为“0”,输出P才为“0”。
由于与或门的输出是从或门引出的,而或门和与门一样,互相联接时也有电平偏离等问题,因此实际应用中很少采用与或门,而常采用“与或非”门。“与或非”门就是在与或门后面再接一个非门,见图5a。它的逻辑关系为:输入端分组先“与”,然后各组再“或”,最后再“非”。显然,其逻辑功能为:当输入端中任何一组全为“1”时,输出即为“0”;只有两组输入端中都至少有一个为0,输出才能为“1”。其逻辑表达式为P=AB+CD-。“与或非”门中的每组与门只用一个输入端时,则“与或非”门便成为“或非”门。
“与或非”门和“与非”门一样,也是一种常用的复合门电路,而且也有定型的集成电路产品。为了便于阅读和绘图,也给它规定了专用的逻辑符号。图5b是一个“ 5—4输入端与或非门”的标准画法,图5c是一个“4—3—2—2输入端与或非门”的标准画法。
“与或非”门可以用作多路信息的公共传送门,见图6。如想将A端信息传送到P端,应使m\(_{1}\)为“1”电平,m2为“0”电平,这样P端信息将取决于A端,即A=1时,P=0;A=0时,P=1。反之,如想送B端信息,则应使m\(_{2}\)为“1”电平,m1为“0”电平。电子计算机中有一种多路开关部件就是采用的“与或非”门。
异或门
异或门也是一种复合门电路,它只有两个输入端,其逻辑功能为:当两个输入端的状态相同(都为0或都为1)时,输出为0;相反时,输出为1。其真值表见图7a,逻辑符号见图7b,逻辑表达式则为P=A-B-。显然,当A=0、B=1时,因为A-B=1,所以P=1;当A=1、B=0时,因为AB-=1,所以P仍为1。而当A=B=1或A=B=0时,P均为0。由于这种电路是两个异号的输入端相加,所以称为“异或门”。
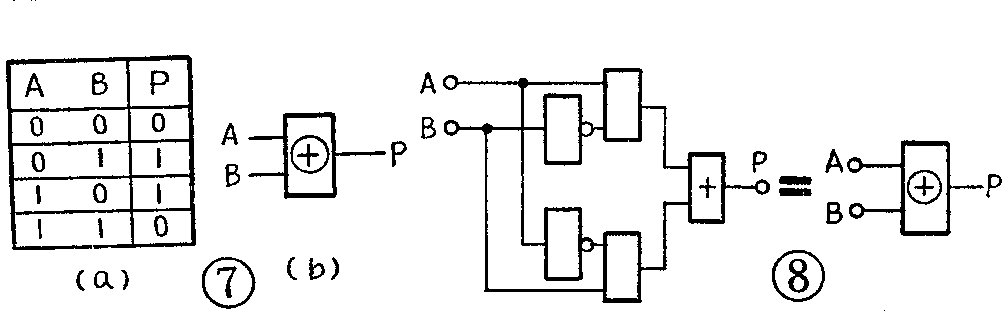
异或门电路可以由基本门电路按逻辑表达式组合而成,图8就是用五个门电路构成的一个异或门电路,其输出和输入的关系完全符合异或门的逻辑表达式,读者可自行分析。也有的把异或门作在一块集成电路中,这时异或门就作为一个单元器件使用。
异或门常用在二进制加法电路中。图9所示的表格就是二进制数的加法规则。如果不考虑进位,只看本位相加的结果,可以发现,被加数、加数和本位和之间的关系,跟异或门的真值表完全相同。这就是说,异或门可以用来作不考虑进位的二进制的加法(进位电路另外考虑,这里从略)。因此异或门又称为“半加器”(同时考虑进位的电路称为全加器),其输出称为半加和。
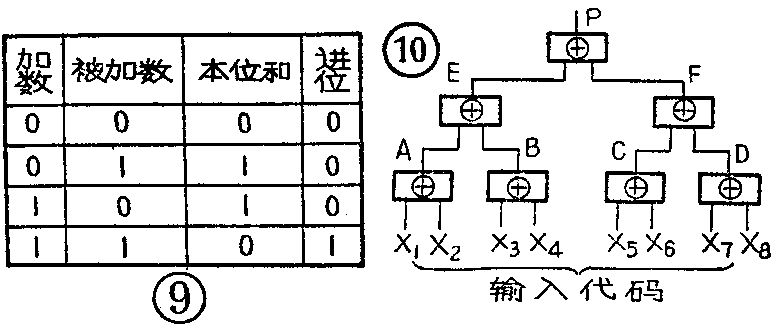
为了检验输入到数字运算系统中的代码信息是否有误,常常使用所谓奇偶校验电路。图10就是使用8单位EIA代码制的奇偶校验电路。输入代码X\(_{1}\)~X8中,每个X不是1就是0,EIA代码规定,只有输入1的个数为奇数才是正确的代码,这时输出P=1。下面我们分析这个电路。当X\(_{1}\)~X8中1的个数为奇数时,根据异或门的逻辑表达式,则A~D中1的个数也是奇数,进而E和F只可能有一个为1,最后P也必然为1。反之,如果代码中1的个数为偶数,则P必然为0,说明输入代码有错。这就达到了检验输入代码的目的。当然,图10作为奇偶校验电路来说并不完整,不过我们的目的是介绍异或门的应用,其它问题在此就不详述了。(方波)