运算放大器最初是由晶体管电路搭成的,主要用在模拟电子计算机中,实现加法、乘法、微分、积分等数学运算。数字集成电路出现以后不久,集成技术便开始应用于模拟电路,于是制造出了集成运算放大器。集成运算放大器的出现,使原来一个十分复杂的电路部件,减小到和晶体管一样大小,并且性能优异,稳定可靠,通用性强,使用方便,因此它早已越出模拟计算机的范围,而广泛地应用在自动控制和测量技术等多种领域中。目前集成运算放大器已经成为电子技术领域中一种基本的放大元件,过去一些电路和系统的设计人员不得不花费很大精力设计、安装和调试放大器电路,现在则只需合理地选择和使用集成运算放大器就可以了。
基本特性
从使用者的角度来说,首先需要了解的是集成运算放大器的基本特性和应用电路。
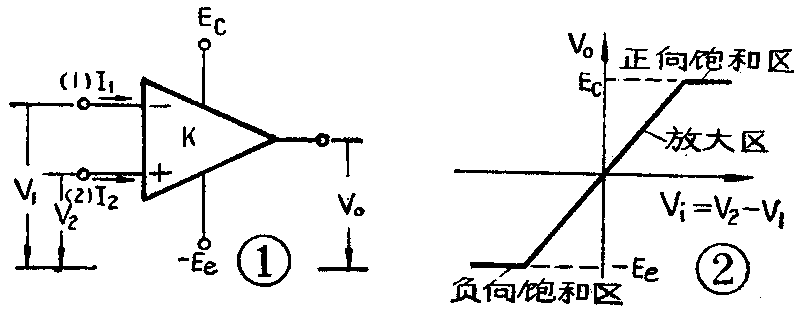
集成运算放大器一般用图1的三角形符号来表示,它有五个引出端:两个输入端(1)、(2);一个输出端;一个正电源端(E\(_{C}\))和一个负电源端(-Ee)。此外,大多数产品还有调零端、频率补偿端和偏置端等辅助引出端。但是在讨论它的基本特性时,先不介绍这些辅助引出端,故图中没有画出。
集成运算放大器实质上是一个高增益的直流放大器,它的输入级几乎无例外地都采用差分放大器,因此它的两个输入端是一对差动输入端。标以“+”号的输入端叫同相输入端,从该端加输入信号,则输出信号与输入信号同相;标以“-”号的输入端叫反相输入端,从该端加输入信号,则输出信号与输入信号反相。既然它的输入级是差分放大器,而它的中间级和末级只是把差分放大器输出的信号再加以放大,因此它的输入输出电压的关系和差分放大器相同,即
V\(_{0}\)=K(V2-V\(_{1}\))……(1)
用文字说明就是输出电压V\(_{0}\)和同相输入端电压V2及反相输入端电压V\(_{1}\)之差成正比。K为比例系数,就是电压放大倍数。其电压放大特性还可用图2的曲线来表示。图2表明,只有在线性放大区内,才能使V0=KV\(_{i}\)(Vi=V\(_{2}\)-V1),当输入差动信号V\(_{i}\)较大时,由于受电源电压的限制,输出电压V0接近电源电压后不能再进一步增加,放大器便进入饱和区。
公式(1)表明了运算放大器也表明了差分放大器的基本特性。但是运算放大器的放大系数K都非常高,可达几万到几十万倍,这是运算放大器和差分放大器的区别。在我们介绍了运放的内部电路以后还会知道,它的两个输入端对地的阻抗也是很高的,一般为几百千欧到几兆欧。因此在实际应用电路中,常常可以把集成运算放大器看成所谓“理想运算放大器”。理想运算放大器的基本特点有两条,一是输入阻抗为无穷大;二是增益为无穷大。根据这两条,我们可以作出如下的重要推论:(1)输入电流I\(_{1}\)、I2都为0(因输入阻抗为无穷大);(2)因为K=∞,而运放的输出电压V\(_{0}\)又总是一个有限值,因此,只要运放工作在放大区而没有进入饱和区,根据公式(1)则有
V\(_{2}\)-V1=V\(_{0}\)/K=0
即运放的两个输入端之间的电位差等于0,或者说同相输入端与反相输入端电位相同。
上述推论虽然是对理想运放来说的,但对于实际的集成运放基本上也是正确的。例如,设某一运放的K=10万倍,当V\(_{0}\)=10伏时,V2-V\(_{1}\)=V0/K=0.1毫伏。这个数值相对于V\(_{1}\)、V2以及V\(_{0}\)来说是很小的,可以忽略不计,可见在放大区内确实可以把运放的两个输入端看作等电位。
理想运算放大器的上述两个特点极为重要,熟练地掌握这两条就能比较容易地分析和理解运算放大器的各种应用电路。下面我们通过几个实例来说明如何利用这两个基本特点分析应用电路。
反相放大器和比例加法器
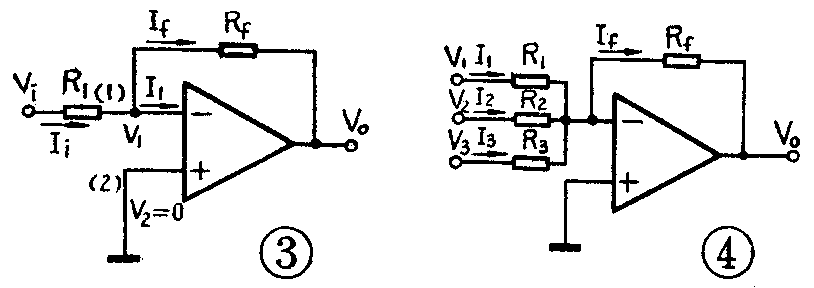
图3是一个基本的反相放大器电路(没有画出正负电源引出端),其输入电压V\(_{i}\)通过R1加到反相输入端(1),其同相输入端(2)接地,而输出电压V\(_{0}\)通过电阻Rf又反馈到反相输入端(1)。设该放大器是理想的,因此I\(_{1}\)=0,V1=V\(_{2}\)。
∵I\(_{i}\)=I1+I\(_{f}\),而I1=0,
∴I\(_{i}\)=If
∵V\(_{1}\)=V2,而V\(_{2}\)接地,
∴ V\(_{1}\)=V2=0伏,于是可以求出下面的式子:
I\(_{i}\)=Vi-V\(_{1}\)R1=V\(_{i}\);Ri
I\(_{f}\)=V1-V\(_{0}\)Rf=-V\(_{i}\);Rf,
V\(_{0}\)/Vi=-R\(_{f}\)/R1……(2)
公式(2)就是该电路的电压放大倍数,其中负号表明输出电压V\(_{0}\)与输入电压Vi相位相反,所以称为反相放大器。显然,该电路的电压放大倍数只取决于电阻R\(_{f}\)与R1之比,而与运放本身的放大倍数K无关。只要改变R\(_{f}\)与R1的比值,就可以获得大于1或小于1的电压放大倍数,具有很大的灵活性,因此该电路广泛应用在各种比例运算中。
以上就是利用理想运算放大器的基本特性分析反相放大器的过程。在这个电路中,虽然(1)端并不象(2)端那样真正接地,然而实际上它总是保持在0电位,因此通常把(1)端称为虚地。为什么这一点能保持0电位呢?这完全是由于电阻R\(_{f}\)提供的负反馈的结果。例如,设R1=R\(_{f}\)=5KΩ,Vi=+5伏,根据公式(2),则V\(_{0}\)=-5伏。显然,这时(1)端处于正、负5伏中间的位置,V1应该为0伏,若V\(_{1}\)不为0,比如说偏正,则V1-V\(_{2}\)>0,由于运放本身的增益很高,因此将会有一个比-5伏负得多的输出电压,这个电压通过Rf反馈到(1)端,就必然使(1)端电位下降,直到V\(_{1}\)=0伏时才能维持稳定。当然,严格地说,为了使运放有一定的输出电压,总需要有一点输入电压,因此V1并非真正等于0伏,只不过十分微小罢了。
在图3中,既然(1)端总保持0电位,于是我们就可以象图4那样,再增加若干组输入信号,而它们产生的输入信号电流可分别表示为
I\(_{1}\)=V1R\(_{1}\),I2=V\(_{2}\);R2,I\(_{3}\)=V3R\(_{3}\)
这些电流在虚地点汇合后流过反馈电阻R\(_{f}\),因此使输出电压为
V\(_{0}\)=-IfR\(_{f}\)=-Rf(V\(_{1}\)/R1+V\(_{2}\)/R2+V\(_{3}\)/R3)……(3)
上式表明,各输入电压按不同比例相加后就等于输出电压。如果R\(_{1}\)=R2=R\(_{3}\)=R,则
V\(_{0}\)=-RfR(V\(_{1}\)+V2+V\(_{3}\))
这就是将几个输入电压信号按相同比例加以组合。如果R\(_{f}\)=R,则输出信号电压为各输入信号电压之和。这是进行比例求和运算的典型电路,叫作“比例加法器”。
积分器电路
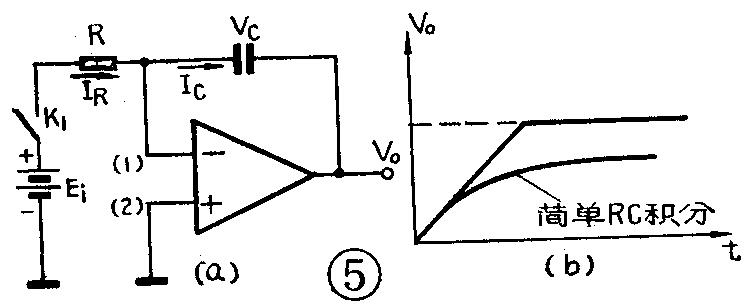
图3中的反馈电阻R\(_{f}\)用电容C代替,就成为积分电路,见图5a。当开关K1接通以后,输入电压E\(_{i}\)便加到电阻R上,输入电流IR=E\(_{i}\)/R,这个电流便是对电容C的充电电流。电容C上积累的电荷Q等于充电电流与充电时间的乘积,因此电容器上的电压VC=Q/C=I\(_{R}\)t/C。而输出电压V0=-V\(_{C}\),所以
V\(_{0}\)=-IRCt=-E\(_{i}\);RCt……(4)
公式(4)表明输出电压V\(_{0}\)随时间t直线增长,直到V0接近于运放的电源电压,达到饱和时为止。输出输入电压的这种关系正好是数学上的积分运算的关系,所以这个电路能够用于积分运算,叫作积分器。
需要说明,V\(_{0}\)所以能够随时间直线上升,正是由于存在着虚地的原因,即(1)端电位总保持为0伏,因而使充电电流IC=I\(_{R}\)=Ei/R维持不变。简单的RC充电电路则不是这样,这种电路在充电过程中随着电容器电压的上升,充电电流越来越小,所以充电电压上升速度越来越慢,而不是和时间成直线关系。两种情况下充电曲线的对比见图5b。
同相放大器
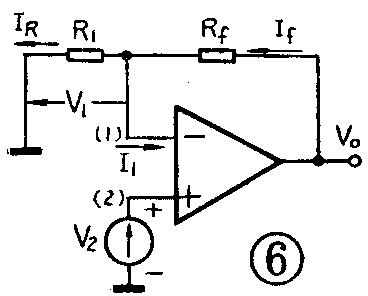
同相放大器的电路如图6所示。信号电压V\(_{2}\)直接从(2)端输入,而输出电压V0通过电阻R\(_{f}\)反馈到(1)端,因此(1)端虽然没有外加输入信号,但仍有电压V1存在,而且V\(_{1}\)=V2。其原因和V\(_{1}\)=V2=0伏时的道理完全相同,读者可自行分析。不过由于这时V\(_{1}\)不等于0伏,所以(1)端不能再叫作虚地。
下面我们分析它的电压放大倍数。由于I\(_{1}\)=0,所以IR=I\(_{f}\),于是得到输出电压V0=I\(_{R}\)(R1+R\(_{f}\)),而IR=V\(_{1}\)/R1=V\(_{2}\)/R1,这样就能求出同相放大器的增益:
把公式(5)和(2)进行比较可以看到,同相放大器的增益也和运算放大器本身的增益无关,而仅取决于外部电阻R\(_{f}\)与R1之比。但是这个数值为正,说明输出与输入电压同相,而且其绝对值也比反相放大器多1。
根据同相放大器输出与输入电压的关系,可以作成同相输入比例器。例如,当R\(_{f}\)=R1时,V\(_{0}\)/V2=2。这就是说,只要在放大区内,不管输入电压怎样变化,输出电压总是输入电压的2倍,两者的比例关系是固定的。(易明銧)