前一节我们介绍过逻辑与(逻辑乘)的代数式为P=AB,逻辑或(逻辑加)的代数式为P=A+B。这两个代数式显然是不同的。为什么呢?因为它们所反映的逻辑电路的功能不同,一个是与,另一个是或。由此可见,不同的逻辑功能要用不同的代数式来表达。与功能、或功能及非功能都是逻辑电路中最基本、最简单的功能,因此它们的逻辑代数式也最简单。但是实际遇到的各种逻辑问题往往要复杂得多(例如数字系统和电子计算机),因此它们的逻辑代数式也就复杂得多。对于复杂的逻辑代数式能不能简化呢?这是摆在我们面前的一个实际问题。此外,有的逻辑代数式虽不能再简化,但是需要变换(电路形式发生变化,逻辑功能不变),这是摆在我们面前的又一个实际问题。实践表明,有些逻辑代数式是能够简化和转换的,而且是有规律可循的,规律就是逻辑代数的基本公式。掌握了这些公式,无论遇到多么复杂的辑逻代数式,都能在一定程度上加以简化,或者根据需要加以交换。本篇就介绍这些基本公式。为便于理解,我们将用开关线路图形象地描述它们的物理意义。
基本逻辑代数式
由上一书讲到的逻辑乘、逻辑加和逻辑非的运算规则,可以直接得到以下的基本逻辑代数式:
0·A=0……(1) 1·A=A……(2)
0+A=A……(3) 1+A=1……(4)
A+A=A……(5) A·A=A……(6)
A+A-=1……(7)
A·A-=0……(8)
A==A ………(9)
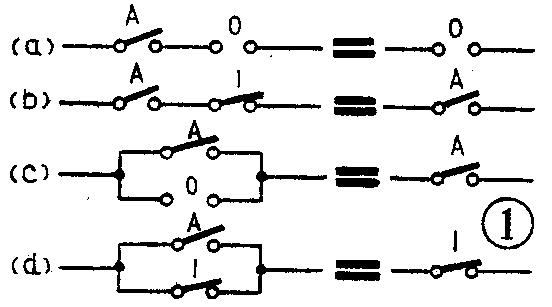
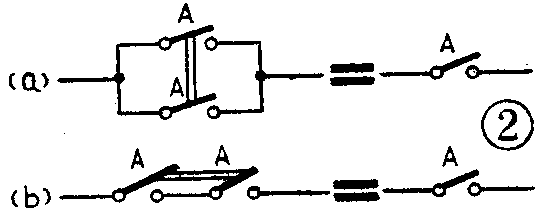
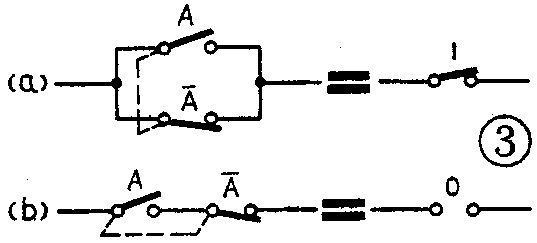
上述公式可以很容易地用与、或、非的运算规则证明,如(1)式中,若A=0,则为0·0=0;若A=1,则为0·1=0。由此可见,0·A=0总是成立的。其它八式也可用同样的方法证明。这样证明虽然正确,但不直观。如果用开关接点线路描述它们,则它们的正确性将是一目了然的。我们仍假设开关闭合为1,断开为0,那么(1)式就表示一个常开接点“0”和开关A相串联(见图1a),显然这个电路是永远不通的,所以0·A=0。(2)式表示一个常闭接点“l”和开关A串联(图1b),很明显。这个电路就等于开关A本身。(3)、(4)二式分别对应于图1c、1d,(5)式对应于图2a,(6)式对应于图2b,它们的意义都很明显,不再叙述。(7)式对应图3a,(8)式对应图3b。图3a是一对并联着的联动开关,但它们两个动作正好相反,一个闭合时,另一个断开,显然这个电路永远是闭合的,所以可用“1”代替。图3b是一对串联着的联动开关,一个合上,另一个就断开,显然这个电路永远是断开的,所以可用“0”代替。(9)式表示对一个逻辑变量“取反”以后再“取反”,根据“反反得正”,结果仍然是这个变量自身。例如,如果开关A是闭合的(A=1),对它取反则断开(A-=0),若再取反则又闭合(A==1)。
与普通代数相同的规律
普通代数的交换律、结合律、分配律在逻辑代数中也成立,实际上这是与、或功能本身的自然结果。
交换律:A+B=B+A……(10)
A·B=B·A……(11)
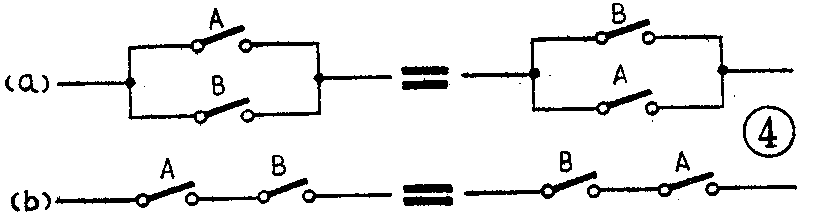
(10)式相应于图4a,由图可知,开关A、B上下对调,结果不变。(11)式相应于图4b,该图描述的是开关A、B前后对调,结果也不变。
结合律:(A+B)+C=A+(B+C)……(12)
A·(BC)=(A·B)·C……(13)
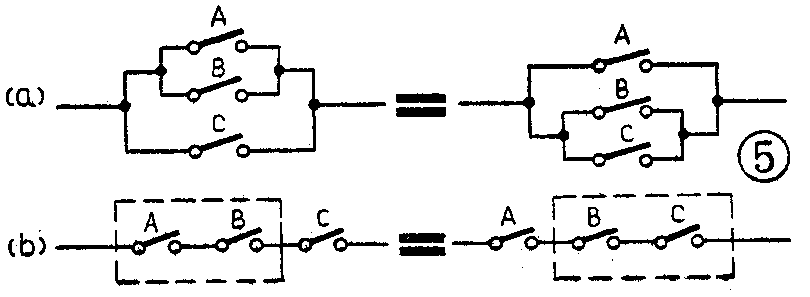
(12)式对应于图5a,(13)式对应于图5b。由图可见,开关A、B、C无论哪两个结合为一组,结果都等效。
分配律:AB+AC=A(B+C)……(14)
该式对应于图6。图中等号左边的电路,无论要哪个支路导通,都必须先将A闭合,显然等号右边也是这样,所以二者等效。
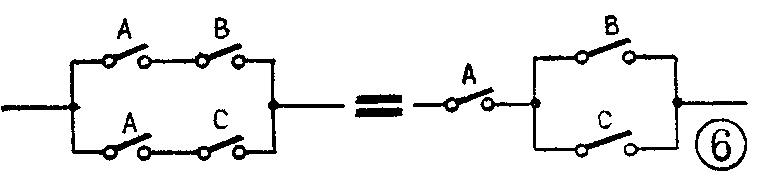
由于以上三个定律适用于逻辑代数,所以我们在处理逻辑代数式时,也可以象处理普通代数式那样,灵活地运用这些定律,这往往给逻辑电路的化简提供很大方便。
特殊规律
逻辑代数终究和普通代数描述的问题有根本区别,因此它有很多不同于普通代数的特殊规律。下面的公式都是逻辑代数所特有的:
A+B-=A--………………(15)
A·B-=A-+B-………………(16)
这是一对经常使用的公式,叫作摩根定理,也叫反演律。它们表示或运算可以转换成与运算,而与运算也可以转换成或运算。这在电路的变换上有很大实际意义。我们知道,与运算和串联电路相对应,或运算和并联电路相对应,因此利用摩根定理就可把串联电路转换成并联电路,或者把并联电路转换成串联电路,这对电路的设计和简化是很有用的。
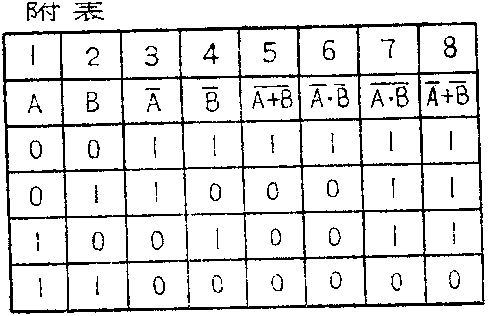
摩根定理的正确性不能再用开关线路图一目了然地看出来。但是可以用真值表证明,见附表。注意式(15)、(16)的每一部分逻辑式都只有两个基本逻辑变量A和B,因此它们都只能有四种组合状态。附表中第5项和第6项的值完全相等,证明(15)式成立;第7项和第8项的值相等,证明(16)式成立。
A+AB=A………………………(17)
A+A-B=A+B…………… (18)
A(A+B)=A …………………(19)
A(A-+B)=AB ……… (20)
以上四式在逻辑电路的化简中也都很有用处。(17)式表示AB项中包含着A,这个AB项是多余的,可以用式(14)、(4)加以证明如下:
A+AB=A(1+B
和(17)式对应的开关线路图为图7a。图中等号两边是等效的,因为A=1时,两边均导通;A=0时,无论B为0还是为1,两边均断开,因此可将A、B串联支路取消,这就简化了线路。
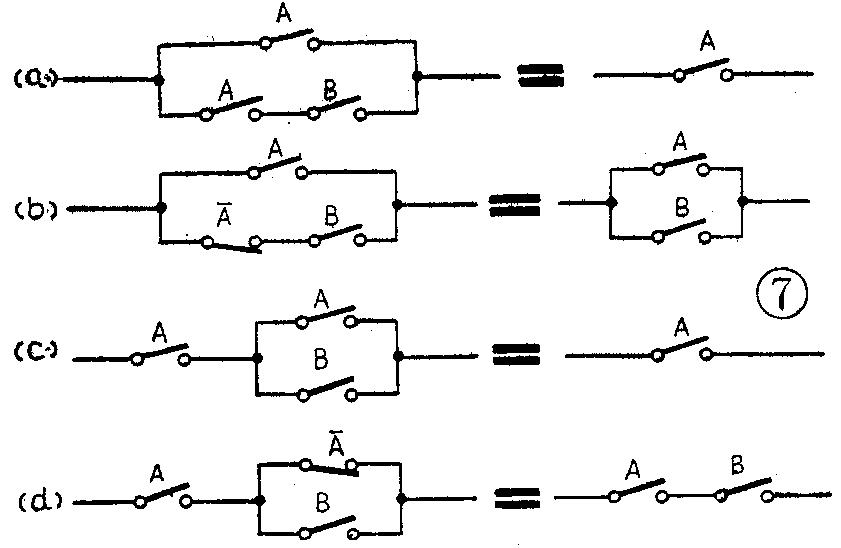
(18)式表示AB项中的A是多余的,可以取消。用(17)、(14)、(7)式可以证明:
A+A-B=A+AB+A-B=A+B(A+A-)=A+B
和(18)式对应的线路为图7b,由图看到,A=1时电路通,A=-必然为1,这时电路通断只决定于B,说明A在任何情况下均无作用故可取消。
(19)式的证明:
A(A+B)=A·A+A·B=A+A·B=A
(20)式的证明:
A(A-+B)=AA-+AB
和它们相对应的线路分别为图7c和图7d,根据前面的经验,读者可自行分析。
上面介绍了逻辑代数的常用公式,这些公式是简化逻辑代数式的有力工具。以后我们将会进一步了解到,具有一定逻辑功能的逻辑线路不是唯一的,可以有繁有简,因此只有利用这些公式进行适当变换,才能设计出具有给定逻辑功能的最简单、经济的线路。关于如何列出代数式及如何利用这些公式进行简化,以后再逐步介绍。(方波)