没有立方根运算键也能开立方吗？

一般型袖珍电子计算器都有平方根键[\(\sqrt{X}\)]和乘方键（按[X\(^{2}\)]或[×] [=]两个键），但没有立方根键。用这样的计算器能否求出一个数的立方根呢？回答是：能！但比一般运算稍复杂些。

我们知道，正数a的立方根记作\(^{3}\)\(\sqrt{a}\)或a1/3。我们假设a\(^{1}\)/3=am/2\(^{n}\),即\(\frac{1}{3}\)=m;2n,并假设n及m均为正整数，具体说，2\(^{n}\)就是这么一些数：2、4、8、16、32……；m就是这么一些数：1、2、3、4、5……。很明显，am/2n=（a\(^{1}\)/2n）m，其中a\(^{l}\)/2n可通过连续开平方n次求出，而（a1/2n）m就是将连续开n次平方后求出的值再进行m次乘方即可。现在要问：n和m取什么值才能使\(\frac{m}{2}\)\(^{n}\)=1;3呢？深入研究一下便知，\(\frac{m}{2}\)n不可能正好等于1;3，在取不同的n、m值时，\(\frac{m}{2}\)\(^{n}\)只能逐步接近1;3。下面写出具体数字看看：

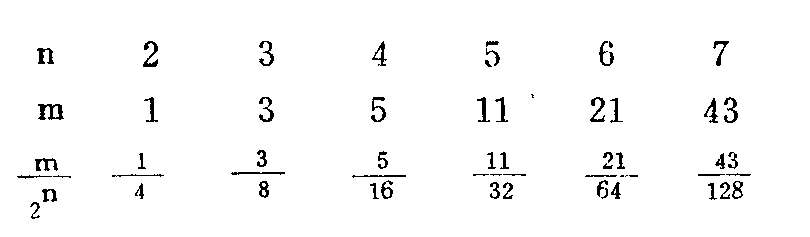
不难看出，\(\frac{3}{8}\)比1;4接近\(\frac{1}{3}\)，而5;16又比\(\frac{3}{8}\)接近1;3……。只要n值取得足够大，并找到适当的m值，就能找到一个数\(\frac{m}{2}\)\(^{n}\)十分接近1;3，其误差可以忽略不计。例如当n=23，m=2796203时，\(\frac{m}{2}\)n与1;3的差值就小于千万分之一。从实用意义来说，只要取适当大的n值就可以了。

m值是怎么确定的呢？很容易。只要将2\(^{n}\)被3除，商数四舍五人取整数就可以了。例如，当n=4时，2n=16，16÷3=5.33……，m则取5。这些运算看起来复杂，实际上使用计算器是很方便的。

总之，解决开立方问题的指导思想就是将开立方的问题化为开平方和乘方的问题，从而扩大了袖珍计算器的应用范围。

我们取n=9，找出用袖珍电子计算器开立方的运算程序。

n=9时，2\(^{n}\)=512，由此求出m=171，即am/2n=a\(^{171}\)/512≈a1/3

我们记a\(^{l}\)/512＝b，则a171/512=b\(^{171}\)因为a1/512＝a\(^{1}\)/29，这就意味着对a连续进行9次开平方运算就得a1/512，即b。我们再把b\(^{171}\)中的指数171表示为以2为底的乘方数，即

就是说对b进行7次连续乘方运算得到b\(^{128}\)，对b进行5次连续乘方运算得到b32等等。再把这5个数（b\(^{128}\)、b32……）连乘就得到b\(^{171}\)。由于这类袖珍机无法把5个数都储存起来，所以中间不得不用手抄。

总结一下获得a\(^{171}\)/512的运算程序是：

（1）输入数 a，按[\(\sqrt{X}\)]9次，显示数N\(_{0}\)=a\(^{1}\)/512＝b，用笔记下N0（显示的数不要清除，下同）；

（2）按[×][=]一次，显示数N\(_{1}\)=N0\(^{2}\)=b2，笔记N\(_{1}\)；

（3）按[×][=]两次，显示数N\(_{2}\)=N1\(^{4}\)=B8，笔记N\(_{2}\)；

（4）按[×][=]两次，显示数N\(_{3}\)=N2\(^{4}\)=b32，笔记N\(_{3}\)；

（5）按[×][=]两次，显示数N\(_{4}\)=N3\(^{4}\)=b128，笔记N\(_{4}\)；

（6）连乘运算：N\(_{4}\)［×］N3[×]=N\(_{2}\)[×]N1[×]N\(_{0}\) 〔=〕显示数N=b\(^{171}\)≈a1/3，这就是要求的结果。

上述运算程序的推导过程虽然比较繁琐，但实际作题时并不要求每次都推导一遍，只要按照已得出的操作程序去作即可。这个运算程序简单易记，只要多练习几次就能熟练运用。下面给出一个实际例子，为清楚起见，就取a=27，即求3\(\sqrt{27}\)\(^{。显然3}\)27=3。

操作时笔记小数点后3位有效数字即可。

连乘的结果就是答案。由于我们取的n值不大，计算结果有些误差，但一般已能满足要求。

从数学上来说，增大n值并选取相应的m值，可使开立方运算精度任意提高，但实际上由于一般袖珍计算器的字长仅8位，若n取得过大，则不仅会由于操作次数太多，使之发生错误的机会增多，并且由于存在着误差积累，运算精度反而会下降。

还有没有更简便的开立方的运算程序呢？如何进一步扩大一般型袖珍计算器的使用范围呢？这是既有趣又有实际意义的问题，请大家来共同思考吧！(吴波)