什么是逻辑代数

编者按：在技术革新和各项工程制作中，逻辑电路的应用越来越广泛。从本期起，我们将陆续介绍一些逻辑代数和逻辑电路的基本知识，供初学者参考。

在谈到什么是逻辑代数之前，先研究一个问题，就是1＋1=？

要回答1＋1=？的问题，首先要弄清“1”代表的是什么，以及它们进行的是什么运算。如果“1”代表的是十进制的数字“一”，那么这个式子表示的就是加法运算，所以1＋1=2，这是幼儿园的小朋友都知道的。二进制只有两个符号0和1，作二进制加法时要逢二进一。因此如果上式的“1”代表的是二进制的数，那么相加的结果是1＋1=10。等号右边的“10”就是用二进制表示的“二”。

以上两种运算都是普通的代数运算，形式虽然不同，但它们所反映的实际内容是一样的：一件东西加一件东西等于两件东西。它们的共同特点是每一个符号（1或0等）都含有“数”的概念，都代表着一个确定的数字。下面我们介绍一种特殊的代数，叫作“逻辑代数”或“开关代数”，也称为“布尔代数”。这种代数虽然也有“代数”两个字，但它和普通代数学的意义却是截然不同的。

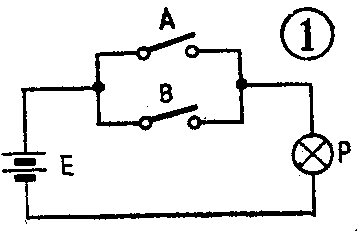
我们先看一个例子。图1中有两个并联开关A和B，很明显，无论是合上一个开关，或两个开关都合上，灯泡都会亮。由此我们可以总结出一种因果关系：决定一件事情的各种条件有一种或几种得到满足时，这件事就能实现。这种因果关系就叫逻辑关系。所谓逻辑就是一定的规律性。这种规律性也可以用代数的形式来表达，这就是所谓的逻辑代数。

上面的问题如何用代数的形式来表达呢？显然，首先必须将问题化成数字的形式，然后再根据问题的性质加上某种运算符号才成。例如，我们可以把某个条件具备了表示为1,不具备表示为0；某件事发生了表示为1，没有发生表示为0。根据这样的规定，那么上述问题中，开关A、B闭合则为1，断开为0；灯P亮为1，灭为0。又因为开关A、B都能独立地把灯点亮，所以可以把它们看成是相加的关系。这样，当合上一个开关而使灯P亮时，可表示成1＋0=1；两个开关都合上，灯P自然也是亮的，这时可表达为1＋1=1。

出现了1+1=1的表达式，这在普通代数中当然是错误的，但这里并不表示数字相加的关系而是表示A合+B合=灯亮这样一种逻辑关系，因此是正确的。

普通代数中可用符号A、B、C等表示变量，由于它们有数的概念，所以可以取从负无穷大到正无穷大之间的任意数值。它们有正负的区别，可以比较大小，运算时有进位、借位的要求等等。逻辑代数也可以用A、B、C等表示变量，但每一个变量只有“0”和“1”两个符号，这两个符号没有数值上的意义，只代表对立统一体中互相矛盾的两个方面或两种状态，可以表示“开”和“关”、“真”和“假”、“好”和“坏”、“是”和“否”、“阳”和“阴”、“正”和“反”、“有”和“无”等等。因为它们没有数量的概念，所以也就没有大小的比较或进位借位的要求。正因为如此，我们把逻辑代数中的“0”和“1”称为“逻辑0”和“逻辑1”。

特别需要说明，二进计数制也只有0和1两个符号，但它们代表的是数字，因此要和逻辑0、逻辑1严格区别开来，不可混淆。

为什么要学习逻辑代数呢？逻辑代数是电子计算机和逻辑电路中进行逻辑判断的重要数学工具。它可以对逻辑电路进行分析和综合。逻辑电路的分析就是已知一个逻辑电路，用描述它的逻辑代数式分析其工作性能，判断它是否经济合理，进而提出改进措施。逻辑电路的综合就是已知工作条件和逻辑性能的要求，求出描述它的逻辑代数式，以设计出最简单、经济的线路。总之，分析和设计逻辑电路，必须熟练地掌握逻辑代数知识，这在以后的学习中会加深体会。

普通代数有加、减、乘、除、开方、乘方等多种运算，而逻辑代数却只有“乘”和“加”的运算，而且它们的意义也和普通代数完全不同。这是由于逻辑代数所反映的客观事物的性质所决定的。为了区别起见，通常把逻辑代数的乘法和加法叫“逻辑乘”和“逻辑加”。此外，逻辑代数还有一种普通代数没有的特殊运算——“非”运算。下面分别加以介绍。

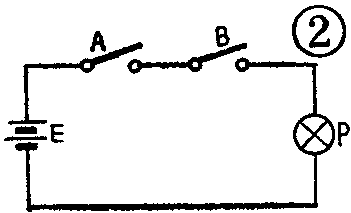
逻辑乘：我们还是先看一个例子，见图2。图中有两个串联的开关A和B，很明显，只有当开关A、B都闭合时灯泡才会亮，有一个开关断开灯泡就不亮。由此我们又可以总结出这样一种逻辑关系：只有当决定一件事情的各种条件都具备时，这件事才能发生。这样的逻辑关系就叫作“逻辑乘”。逻辑乘又称为“逻辑与”，意思是只有A“与”B两个条件全具备才成。我们仍规定“1”表示灯泡P亮，“0”表示灯泡P灭；开关A、B合上为“1”，断开为“0”，则图2中P与A、B间的关系可以用表1来表示。表1中横着的第一行表示A断、B断、P灭；第二行表示A断、B合、P灭；第三行表示A合、B断、P灭；第四行表示A合、B合、P亮。不难看出，表1反映的P与A、B的关系与普通代数的乘法规则在形式上相同，借用普通代数的符号，则P与A、B间的“乘”逻辑关系可记为：

这就是逻辑乘运算。其运算规则显然为：

逻辑加；图1所举的例子就是“逻辑加”，这里不再重复。逻辑加又叫“逻辑或”，意思是条件A“或”B只要有一个具备就成。同样，我们也可以把图1中P与A、B的关系列成表（见表2）。表2中横着的第一行表示A断、B断、P灭；第二行表示A断、B合、P亮；第三行表示A合、B断、P亮；第四行表示A合、B合、P亮。也不难看出，表2反映的P与A、B间的关系与普通代数的加法规则在形式上有相似之处，借用普通代数的符号，则P与A、B间的“加”逻辑关系可记为：

这就是逻辑加运算。其运算规则为：

只有最后一式（1＋1=1）和普通代数加法在形式上不同。

必须注意，在逻辑加法中，因为事件的结果只能在“0”和“1”两种状态中选择一种，所以不管有多少个“1”相加，其逻辑和也只能是“1”。例如，如果图1不是两个开关，而是更多的开关并联，而且这些开关全闭合（即有多个1相加），其结果也只能是使灯亮，即P=1。

逻辑非：逻辑非也叫逻辑否。对一个逻辑变量进行“非”运算，就是对这个变量从逻辑上予以否定，或者说对这个变量“取反”。例如，对“真”的否定就是“假”，对“是”的否定就是“非”，对“高”的否定就是“低”，对“有”的否定就是“无”等等。

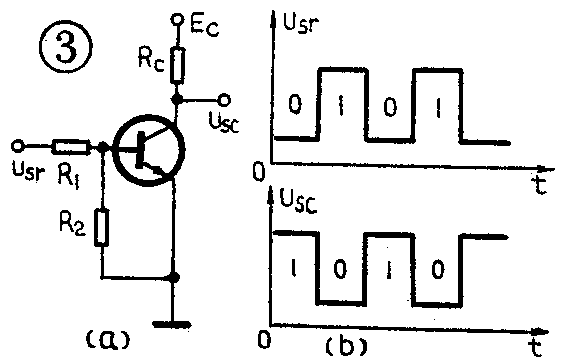
有一种电路叫反相器，见图3a。当这个电路的输入电压U\(_{sr}\)很小时（小于0.5伏），晶体管是截止的，这时输出电压Usc等于电源电压；当输入电压U\(_{sr}\)较大时（0.7伏以上），晶体管导通，适当选取R1，R\(_{2}\)、Rc的数值，可使晶体管饱和。晶体管的饱和压降即输出电压近似为0.3伏。由此可见，该电路具有如下的特点：输入为低电平时，输出为高电平；输入为高电平时，输出为低电平（见图3b）。如果用“1”代表高电平，“0”代表低电平，那么它的输入与输出的关系则为入=1时，出=0；入=0时，出=1。这是最常见的一个逻辑非电路。

逻辑非运算有它的特殊符号，就是在变量上加一短横“—”，如A-，读作非A。它的运算规则是：

因此，如果P=1，则P-=0。

最基本的运算就是这三种。从这三种运算可以演化出很多重要公式，这些公式对分析逻辑电路和了解电子计算机的工作原理都是极有用的。

我们在介绍逻辑乘的时候，列出了表1。表1中横着的每一行数字构成一组，叫作输入变量的一种组合状态。表一一共是四行数字，所以共有四种组合状态。进一步研究表明，由于每一个输入变量只能取0和1两个值，所以具有两个输入变量的逻辑乘的组合状态只能有这四种，此外再无别的组合状态。

像表1那样，如果把某一逻辑代数式的输入变量的各种可能的组合状态和输出变量之间的逻辑关系都写出来，并排成表格，则这种表格就叫作“真值表”。上述表1就是有两个输入变量的逻辑乘的真值表，表2是有两个输入变量的逻辑加的真值表。逻辑非只有一个输入变量，它的真值表如表3所示。

对逻辑乘和逻辑加来说，有两个输入变量时，由于每个变量能取两种状态，所以共有2×2=2\(^{2}\)=4种组合。如果是三个输入变量，真值表就该有2×2×2=23=8种组合。以此类推，如果n个输入变量（n＝1、2、3……），则该有2\(^{n}\)种组合。

真值表是进行逻辑设计的重要工具。例如，利用真值表可以对逻辑式进行验证或对电路进行简化，也可以按设计要求，根据真值表列出逻辑式和设计电路。关于真值表的应用，以后还要结合实例详细介绍。(方波)