我们把晶体管用作放大或振荡时,它的工作频率是有一定限度的,如果超过这个限度晶体管的放大倍数就要下降,乃至完全失去工作能力。这是什么原因呢?我们知道晶体管的电流(载流子)是由发射结发射,经基区输运、集电结收集输送到外电路的。其中发射结、集电结两个p—N结都具有电容效应(P—N结都有结电容)。因此当电信号经过晶体管时有一个渡越时间,也就是说当电流流经晶体管时会产生延迟(相移)。当信号频率较低时,这些因素可以忽略掉,所以放大能力不受影响,但当信号频率较高时,载流子的渡越时间与信号周期相比就不能忽略了,高频时晶体管的结电容呈现较低的阻抗,使一部分信号旁路了,这就降低了发射结输入效率和集电结的收集效率,于是使输出信号不仅在时间上有所延迟,而且在幅度上也下降了。当信号频率再提高时,这个现象就更严重了,甚至可能出现注入的多数载流子在尚未到达集电区时,输入信号的幅度和方向却开始变化了,造成载流子运动紊乱现象,以至使晶体管完全失去工作能力。
随着工作频率的升高,所有晶体管的放大能力都会下降,但不同晶体管放大能力开始显著下降的频率是各不相同的。例如有一些晶体管(低频管)的放大能力在10千赫左右就开始下降,另一些管子(高频管)的放大能力在几兆赫或几十兆赫才开始下降,还有一些管子(超高频管或微波晶体管),可以一直工作到几百兆赫甚至几千兆赫。这就是所谓的晶体管频率特性。为了表明不同晶体管的不同的频率特性,在手册上除了标出直流参数和极限参数之外还需要增设频率参数。通常晶体管的频率参数有f\(_{α}\)、fβ、f\(_{T}\)、fm。下面我们就分别介绍这几个参数。
1.f\(_{α}\)——共基极截止频率(α截止频率),在共基极电路中,电流放大系数α值在工作频率较低时基本为一常数。当工作频率超过某一值时,α值开始下降,当α值下降至低频值α0(例如f为1KHz)的1\(\sqrt{2}\)(即0.707倍)时所对应的频率为f\(_{α}\),称为共基极电路截止频率或α截止频率。
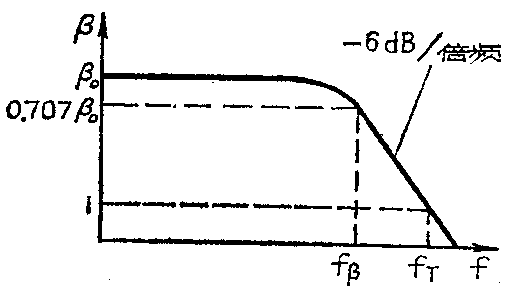
2.f\(_{β}\)——共发射极截止频率(β截止频率),与fα类似,在共发射极电路里电流放大系数β值在降低到低频值β\(_{0}\)的1\(\sqrt{2}\)时所对应的频率称为共发射极截止频率(见图1)。
上述两个截止频率的物理意义是相同的,即α和β相对于低频值下降1\(\sqrt{2}\)时的频率,区别仅在于晶体管在电路中的连接方式不同,因而频率特性也有所不同。理论和实验都证明同一只晶体管的f\(_{β}\)值远比fα值小,这两个参数有如下的关系:f\(_{α}\)=(1+β)fβ。一般规定f\(_{α}\)<3MHz的晶体管称做低频管,fα>3MHz的称做高频管。低频晶体管的频率参数常用f\(_{α}\)或fβ表示,在晶体管手册中往往只给出其中一个,但有了上述的关系式,知道了其中一个频率参数即可推算出另一个频率参数。例如已知一个晶体管的f\(_{α}\)是500KHz,β为1000,那么fβ=f\(_{α}\);1+β≈5KHz。
在实际使用中,工作频率即使等于f\(_{α}\)或fβ并不等于管子“截止”不能工作,仍可有相当的放大能力。例如某晶体管β在1KHz时测试为100(即β\(_{0}\)=100),当f=fβ时β=100\(\sqrt{2}\)=70.7,这就是说该晶体管在f=f\(_{β}\)工作时仍有相当高的放大倍数。但在设计电路和使用晶体管时,若要使电路有较高的工作频率,应尽量选用fβ(或f\(_{α}\))高的管子。如果要使放大器的工作频率大于10KHZ,考虑到电路的反馈,那么应选fβ>8KHZ的管子为好。一般β高的管子f\(_{β}\)也高一些,所以对于同一个电路,挑β高些的管子,工作频率也可提高一些。由于α值在较宽的频率范围内比较均匀,且fα远大于f\(_{β}\),所以高频宽带放大器和一些高频、超高频、甚高频振荡器常用共基极接法。
3.f\(_{T}\)——特征频率如前所述晶体管工作频率超过一定值时,β值开始下降,当β下降为1时,所对应的频率就叫做特征频率fT。当f=f\(_{T}\)时,晶体管就完全失去了电流放大功能。fT是设计晶体管或使用晶体管时必须考虑的一个参数。有时f\(_{T}\)也称为增益带宽乘积。
4.f\(_{m}\)最高振荡频率——由于一般晶体管的输出阻抗总比输入阻抗要大,因此即使是β=1或小于1它还可能获得功率放大。例如有些微波晶体管就是在接近fT或超过f\(_{T}\)的频率下获得功率增益的。为了说明晶体管工作频率上的限制,又定义功率增益等于1时的频率称为晶体管的最高振荡频率fm,当f=f\(_{m}\)时,功率放大倍数等于1,其意义即是晶体管电路在这个频率下振荡时,输出端全部功率反馈到输入端时刚好可以维持振荡工作状态,频率再高一点即停止振荡。
为了使用上方便,一般高频或超高频晶体管的频率参数都用f\(_{T}\)和fm来表示,其中f\(_{T}\)的使用最为普遍。在图一中我们可以看出,当频率f增加到一定程度时,β就开始下降,当工作频率大于fβ时,这时β值与频率成反比,这就是通常称的β以-6分贝/倍频下降规律。这时频率每升高一倍,β值就比原值小一倍,所以频率f与对应的放大系数β乘积是不变的即f·β=常数,这个常数就是f\(_{T}\)。根据这个关系式,我们便可以灵活地加以应用。现举二例说明:
1.间接测量f\(_{T}\):对于一些高频或超高频管,fT相当高,往往在几百兆赫以上,如要直接测量f\(_{T}\)则需用超高频仪器,因而给测试带来一定的困难。这时我们可以大致选择一个频率f,使f大于fβ(根据所测管类型试选)。测出该频率时的β,即可算出f\(_{T}\)=f·β。目前不少测fT的仪器都采用这种方法。
2.间接测量高频下的β值:业余爱好者在装电视机高频头时,需要了解晶体管在高频状态下的放大性能。一般经验是,最高工作频率时β>3或者f\(_{T}\)大于工作频率的三倍就基本合用。例如要了解某一高频管在190MHz(8频道)时的放大倍数,我们可以先测出此管在较低频率f1(大于f\(_{β}\)的频率)时的β1,再由f\(_{1}\)β1=f\(_{2}\)β2=常数(f\(_{T}\))就可推算出f2=190MHz时的β\(_{2}\)。例如某高频管3DG56B在f1=30MHz时测出β\(_{1}\)为46,β2=\(\frac{f}{_{1}}\)β1f\(_{2}\)=30×46;190≈7,该管合用。再如已知某高频管3DG84D的fT=1150MHz,由f\(_{T}\)=f·β,β=fTf=1150;190≈6,该管也合用。(张顺颐 李锦春)