如何设计逻辑电路

(杨廷善)本刊1979年第4期刊登的《消0法》一文，有不少读者提出电路还可以简化，并从逻辑电路的分析方法和设计方法入手进行了讨论，现选登其中一篇，供参考。

对于逻辑问题的描述，逻辑电路的分析和设计，逻辑代数是非常有用的数学工具。这篇短文不可能系统地介绍逻辑代数，只是打算借助它的某些内容，结合消0问题，向读者介绍逻辑电路的一般设计方法，以便进而引起读者对以逻辑代数为工具解决逻辑问题的兴趣。

现以《消0法》一文中四位数的消0电路为例，说明设计逻辑电路的方法和步骤。

第一步。对所提出的问题进行分析，并用条理分明的、严谨的语言加以描述。对于本例，其描述如下：

1．千位0，在任何情况下，均不应出现。

2．个位的0，在任何情况下，均应出现。

3．十位的0是否出现，有三种情况：

①十位是0，千位和百位也都是0，这时十位的0不应出现。

②十位是0，但千位和百位不同时为0，这时十位的0应出现。

③十位不是0，这时十位当然不应出现0。

4.百位的0是否出现，有三种情况：

①百位是0，千位也是0，这时百位的0不应出现。

②百位是0，但千位不是0，这时百位的0应出现。

③百位不是0， 这时百位当然不应出现0。

第二步。对以上描述，结合译码、显示电路再进行分析，画出待求消0电路的框图；同时将待求消0电路的输入和输出间的关系用表格形式写出（此表称为真值表）。

对于本例，译码器在译0数字时，译码部分的与非门0输出为高电平（即“1”）；反之，在译非0数字时，与非门0输出为低电平（即“0”）。见图1（即《消0法》中图1）。

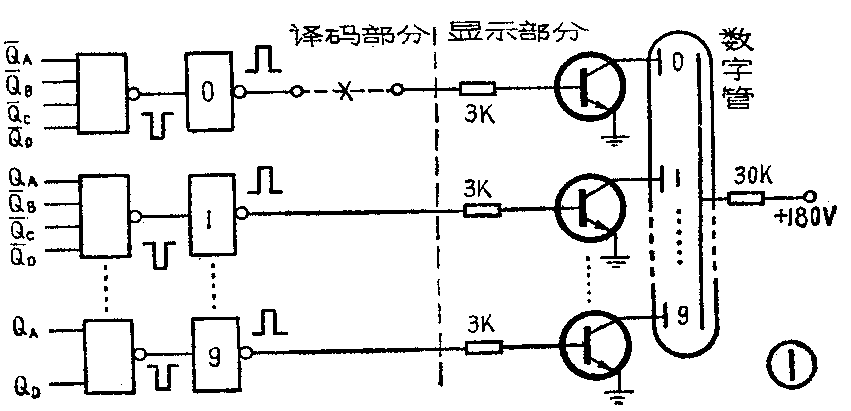
1．千位的0既然永不出现，故只要将数码管字符0的电路断开即可。

2．个位的0既然永远出现，故电路不加改动。

3．十位的0是否出现与千位、百位及十位的情况

有关。百位的0是否出现与千位及百位的情况有关。

上述分析归结为图2。

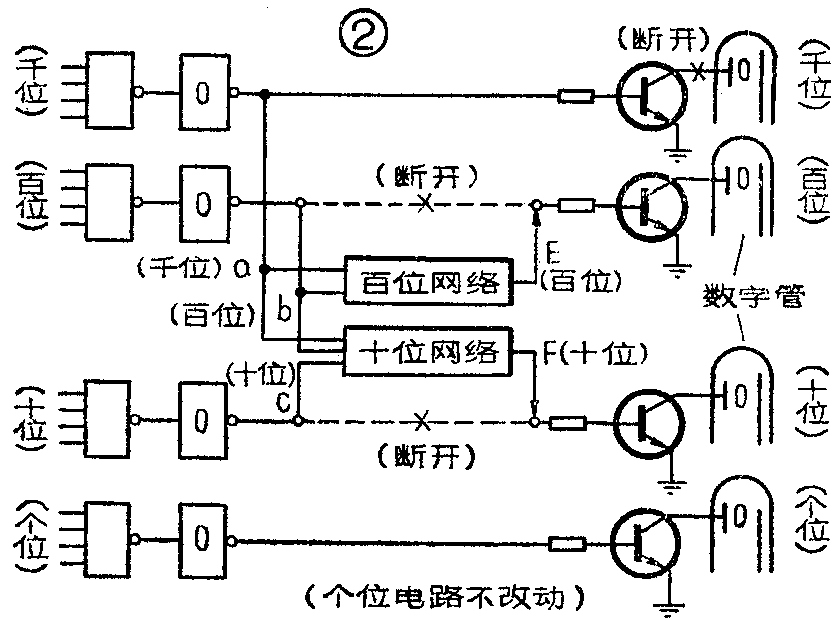
至此，问题变成为求百位网络和十位网络内的具体电路。这两个网络的输入信号与输出信号之间的关系，已在第一步中详细说明过，现将这些关系列成表格（真值表）如表1。

列表的具体法则如下：

1．将输入端a、b和c可能出现的电平值的组合全部列出，共2\(^{3}\)=8种。

2．写出输出瑞F（十位）的电平值：

①由第一步中第3之①项，得出第八行应为“0”。

②由第一步中第3之②项，得出第二、四和六行应为“1”。

③由第一步中第3之③项，得出第一、三、五和七行应为“0”。

3．写出输出端E（百位）的电平值：

①由第一步中第4之①项，得出第七和第八行应为“0”。

②由第一步中第4之②项，得出第三和第四行应为“1”。

③由第一步中第4之③项，得出第一、二、五和六行应为“0”。

第三步。由真值表写出待求电路的逻辑表达式：

1．表达式是一个多项式，其项数等于输出端中具有高电平“1”的行数。本例：E有二项，F有三项：

2.输入端变量中，高电平“1”表示正变量（不加非号）；低电平“0”表示反变量（加非号）。

3．表达式中的每一项，为输出端出现高电平的那一行的输入变量的乘积。对于本例，表达式如下：

第四步。化简逻辑表达式（在此要应用逻辑代数中的法则，本文不详述），可得：

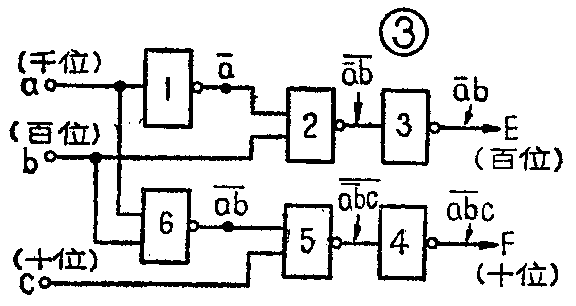
第五步。由最简逻辑表达式画出逻辑电路图。在本例中全部使用与非门，可用逐级推导法画出，如图3。