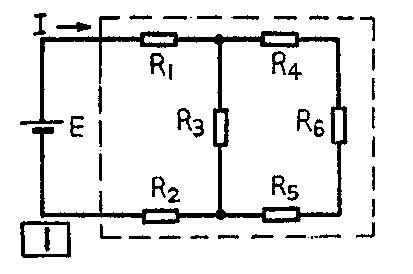
这些电阻合起来有多大
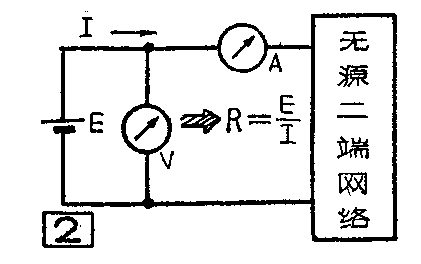
当我们看电路图时,常看到一个电源所接的负载是由好几个电阻串联或并联组成的(图1)。这些电阻合起来有多大呢?最方便的计算方法,是假设这些电阻都封闭在一个盒子里,只引出两根线头。盒子里这部分只有电阻没有电源的电路称为“无源二端网络”(图2),我们可以先不去管二端网络里的电阻有多少个,也不管它们是怎样联接起来的,只要测出网络两端的电压和流入网络的电流,用欧姆定律就能方便地计算出“总电阻”
或者也可以把电源断开,将欧姆表接在两根引出线上,直接测量出总电阻R,这个总电阻称为无源二端网络的等效电阻。任何一个无源二端网络,都可以用一个等效电阻R来代替它,下面就来谈谈怎样计算串联和并联电阻的等效电阻。
串联电阻的等效电阻
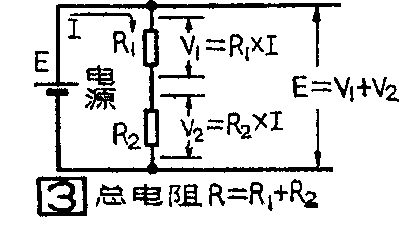
如果把两个电阻R\(_{1}\)和R2串联起来,接到电压为E的电源上(图3),则流过回路的电流I将分别在R\(_{1}\)和R2两端产生电压降。根据欧姆定律
R\(_{1}\)上的电压降 V1=R\(_{1}\)I
R\(_{2}\)上的电压降 V2=R\(_{2}\)I
这两个电压降V\(_{1}\)和V2是由电源电压E提供的,E=(R\(_{1}\)I)+(R2I)=(R\(_{1}\)+R2)I。
如果我们想象自己是站在电源的地位向电路中看去,电源E所引起的电流是I,那么根据欧姆定律,就能算出由R\(_{1}\)和R2组成的无源二端网络的等效电阻
R=\(\frac{E}{I}\)=(R\(_{1}\)+R2)I;I=R\(_{1}\)+R2
当串联电阻不止两个时,也可以用同样的方法来计算
R=R\(_{1}\)+R2+R\(_{3}\)+……+Rn
这就是说,串联电阻的等效电阻,等于各个电阻的和。
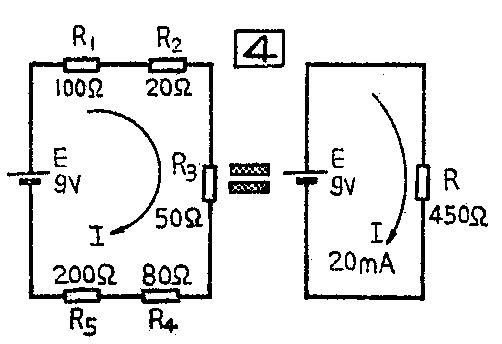
我们用图4做例子,说明电阻串联电路的计算方法。这个电路一共有五个电阻串联,R\(_{1}\)=100Ω,R2=20Ω,R\(_{3}\)=50Ω,R4=80Ω,R\(_{5}\)=200Ω。等效电阻R=R1+R\(_{2}\)+R3+R\(_{4}\)+R5=450Ω。这就是说,图4虚线框内的无源二端网络,对电源E来说,可以等效为一个450Ω的电阻R。用欧姆定律可以算出流过回路的电流
I=E/R=9V/450Ω=0.02A=20mA
再来看电源电压在各个电阻上是怎样分配的:
R\(_{l}\)两端的电压=10OΩ×0.02A=2V
R\(_{2}\)两端的电压=20Ω×0.02A=0.4V
R\(_{3}\)两端的电压=50Ω×0.02A=1V
R\(_{4}\)两端的电压=80Ω×0.02A=1.6V
R\(_{5}\)两端的电压=200Ω×0.02A=4V
这些电压的总和等于电源电压:9V。它表明电阻串联电路的电源电压等于各电阻上电压降之和。
并联电阻的等效电阻
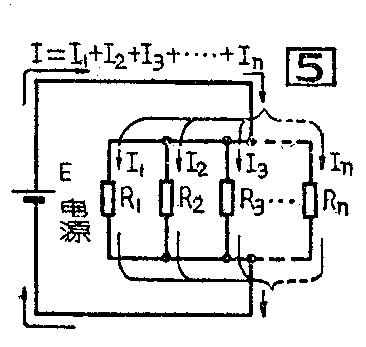
在电阻并联电路中(图5),各个电阻两端的电压都相等,而从电源正极流出的电流,在各电阻支路会合的一点(称为节点)分开,流入各电阻支路。各支路的电流,又在另一个节点会合起来,返回电源的负极。显然,各并联支路电流的总和,就等于从电源送出的总电流,即
I=I\(_{1}\)+I2+I\(_{3}\)+……+In
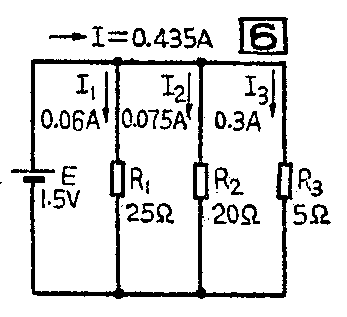
因为各个并联电阻的端电压都等于E,所以用支路电阻去除E,就能求出各支路上通过的电流。以图6为例,三个并联电阻分别为:R\(_{1}\)=25Ω,R2=20Ω,R\(_{3}\)5Ω;电源电压E=1.5V。
流过R\(_{1}\)的电流I1=1.5V/25Ω=0.06A
流过R\(_{2}\)的电流I2=1.5V/20Ω=0.075A
流过R\(_{3}\)的电流13=1.5V/5Ω=0.3A
电源提供的总电流I=I\(_{1}\)+I2+I\(_{3}\)=0.435A。
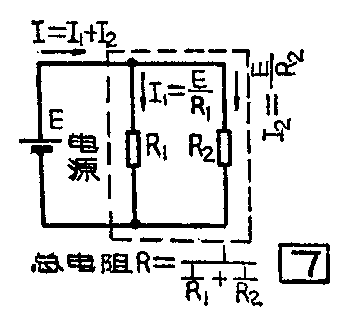
几个电阻并联组成的也是一个无源二端网络。怎样求并联电阻的等效电阻呢?我们先用一个最简单的两个电阻并联的电路来分析,如图7所示,流过R\(_{1}\)和R2的电流I\(_{1}\)和I2分别为
I\(_{1}\)=\(\frac{E}{R}\)1,I\(_{2}\)=E;R2
I\(_{1}\)和I2是由总电流I来供给的,因此有
I=I\(_{1}\)+I2=\(\frac{E}{R}\)\(_{1}\)+E;R2=E×(\(\frac{1}{R}\)\(_{1}\)+1;R2)
因无源二端网络的等效电阻为R=\(\frac{E}{I}\)
将前面求得的总电流I代入上式,便可得
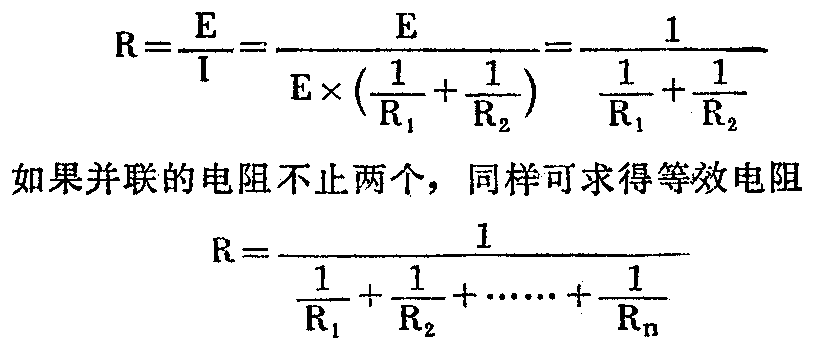
这里,我们再做两个例题,熟悉一下电阻并联电路的计算方法。
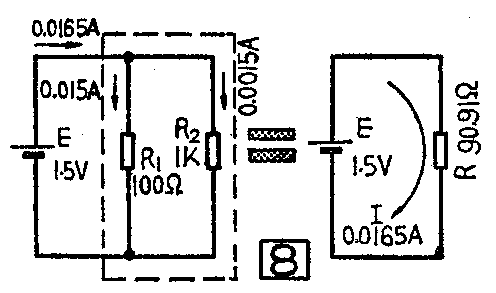
图8是两个电阻并联的电路,R\(_{1}\)=100Ω,R2=1KΩ,等效电阻为
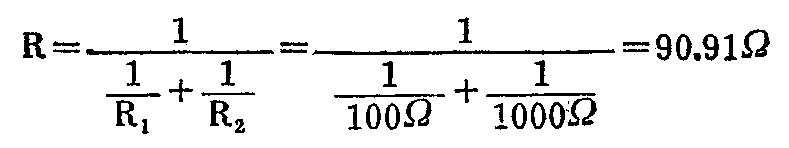
流过这两个电阻的电流分别是
I\(_{1}\)=1.5V/100Ω=0.015A
I\(_{2}\)=1.5V/1000Ω=0.0015A
从这个例子可以看出,如果需要一个比原来电阻的阻值减少10%的电阻,可以并联上一个比该电阻大10倍的电阻。在我们做实验时,有时手头上没有阻值合适的电阻,就可以用串联或并联的方法凑出所需要的阻值。
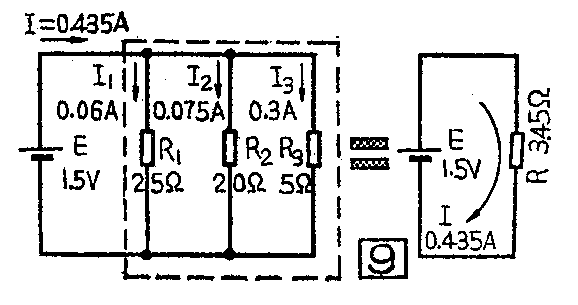
图9是三个电阻并联的电路。可以算出它的等效电阻
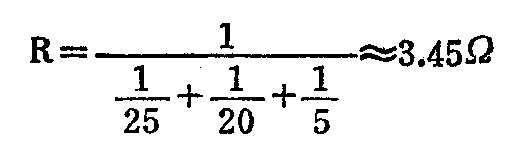
可以看出,并联电阻的等效电阻比各并联电阻中最小的电阻还要小。
混联电阻的等效电阻
实际的电阻混联电路,可能相当复杂,但只要将它们划分成许多基本的串、并联回路,再用串、并联电路的计算公式一步一步地进行计算,最后就不难求出等效电阻来。
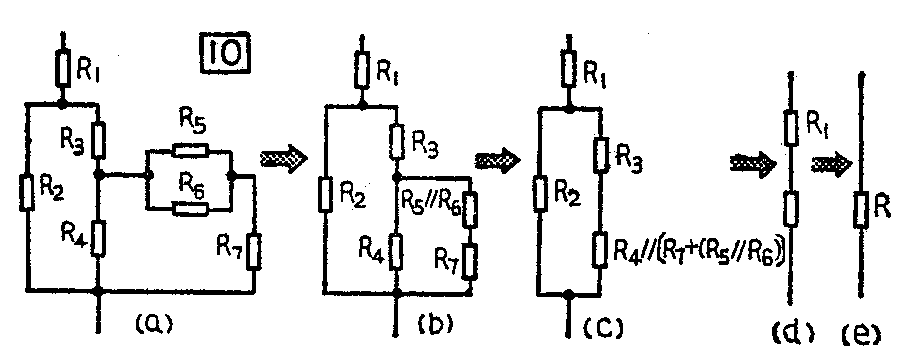
让我们分析一下图10所示的电阻混联电路。这里一共有7个电阻,可以按下面的步骤求出它们的等效电阻。
(1)电阻R\(_{5}\)和R6是两个并联的电阻,用符号“‖”表示并联,可以求出R\(_{5}\)和R6并联的等效电阻为
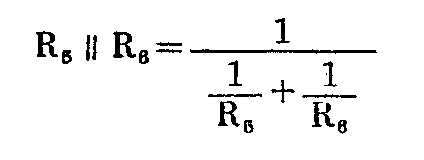
(2)R\(_{7}\)与R5‖R\(_{6}\)是串联关系(图10b),这条支路的总电阻为R7+(R\(_{5}\)‖R8),再与R\(_{4}\)并联,其等效电阻为
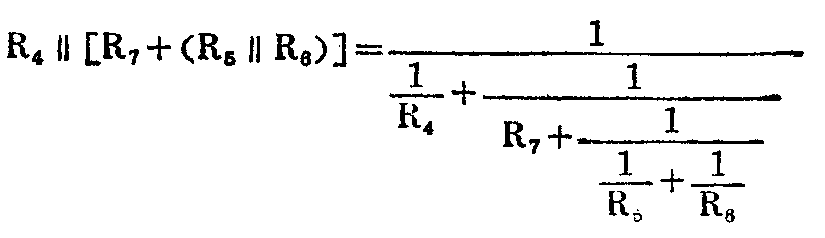
(3)由图10c可见,R\(_{4}\)‖[R7+(R\(_{5}\)‖R6)]与R\(_{3}\)是串联关系,然后再与R2并联,计算出它们的等效电阻,就得到图10d的等效电路。
(4)将图10d的串联电路再进行简化,就能求出这7个混联电阻的等效电阻R(图10e)。
戴维南定理
如果有一个比较复杂的电路,我们仅需要求出其中某一条支路的电流,应用下面介绍的戴维南定理进行计算是比较方便的。
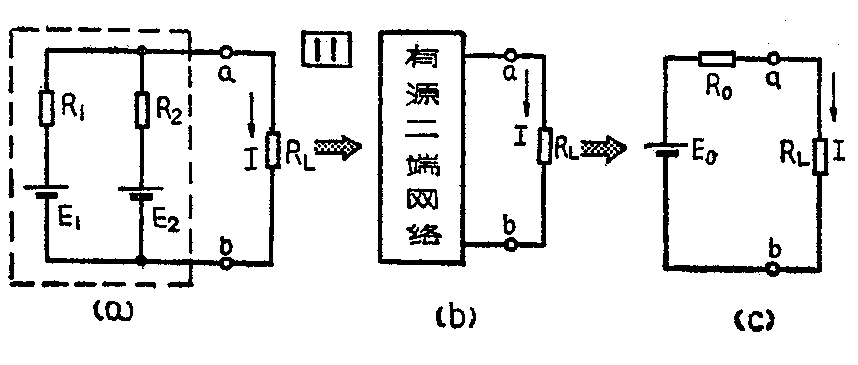
例如在图11a所示的电路中,我们所要计算的只是流过电阻R\(_{L}\)上的电流,就可以把RL以外的电路用方框围起来,接出两个引出端a和b,方框内包含着电源和电阻的这部分电路,称为有源二端网络(图11b)。任何一个有源二端网络,对外电路来说,都可以等效为一个具有电势E\(_{0}\)和内阻R0的电源,称为等效电源。求E\(_{0}\)的方法是:把支路RL断开,测量或计算出有源二端网络在开路时的端电压,它在数值上等于E\(_{0}\)。R0的求法是:假设网络内所有的电源都短路,就成了一个无源二端网络,然后用前面介绍过的电阻串、并联电路的计算方法,算出网络的等效电阻就是R\(_{0}\)(图11c)。流过电阻RL的电流为
I=E\(_{0}\)R0+R\(_{L}\)
以上就是戴维南定理,也叫等效电源定理。
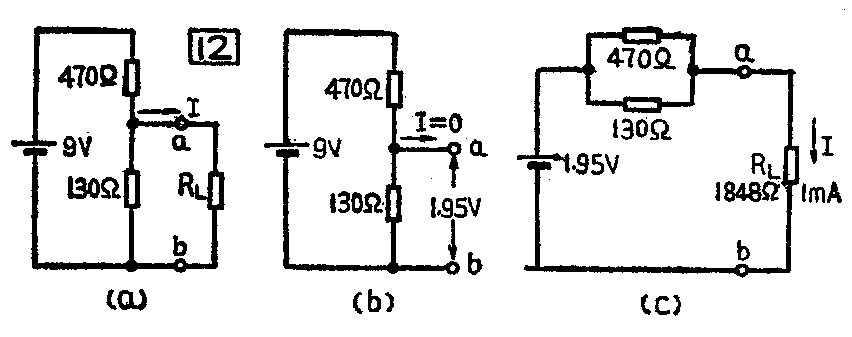
下面,我们用戴维南定理来计算图12中R\(_{L}\)支路的电流I,计算步骤如下:
(1)把支路RL断开,求出有源二端网络开路时的端电压值
V\(_{ab}\)=9V×\(\frac{130Ω}{470Ω+130Ω}\)=1.95V
E\(_{0}\)=Vab=1.95V
(2)假设有源二端网络内所有电源都短路,求出内阻R\(_{0}\)=470Ω‖130Ω=102Ω。
(3)计算流过RL的电流,已知RL=1848Ω
I=\(\frac{1.95V}{102Ω+1848Ω}\)=1mA
于是,就可以算出接上负载R\(_{L}\)以后,a、b两点间的电压
V′ab=1\(_{mA}\)×1848Ω=1.848V
(张学志 颜超 宋东生 编译)