在导体的两端加上电压,就能产生电流,电流流过导体,又不可避免地会遇到电阻。那么,电压、电流和电阻这三个基本电学量之间究竟存在着什么关系呢?1827年德国科学家欧姆,经过大量的实验,解答了这个问题,总结出一个最基本的电路定律—欧姆定律。欧姆定律指出:当导体温度不变时,通过导体的电流与导体两端的电压成正比,与导体的电阻成反比。
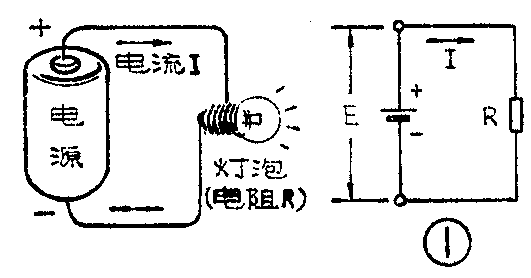
用图1这样的一个简单电路为例:如果将电压为E伏特的电源,加在电阻为R欧姆的负载上,则电流为I安培。它们的关系是:电流〔A〕=\(\frac{电压〔V〕}{电阻〔Ω〕}\),即I=E;R
例如,在5Ω电阻的两端加10V电压,那末流过电阻的电流就等于10V5Ω=2A。
欧姆定律还可以写成下面的形式:
电压〔V〕=电阻〔Ω〕×电流〔A〕以及电阻〔Ω〕=
电阻上的电压降
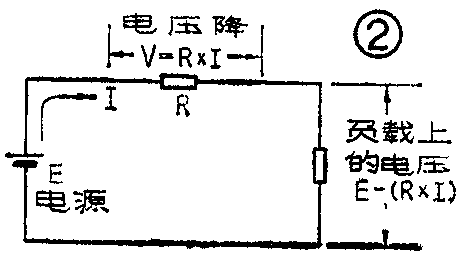
大家知道,电路中的电流是依靠外加电压做原动力才能流动的。为了让电流通过电阻,就得有一部分电压“损耗”在电阻上。我们把电流通过电阻时,降落在电阻两端的电压,叫做电压降。图2中电流I在电阻R上产生的电压降就是V=RI,负载上实际得到的电压,只剩下E-RI了。可以看出,只要电路中有电阻,就有电压降存在,电源电压就不能有效地全部加到负载上去。
我们举个实际例子计算一下(图3)。把一只电炉接到100V的电源上去,倘若电炉丝中通过10A的电流,而每条引线的电阻是0.5Ω,则:
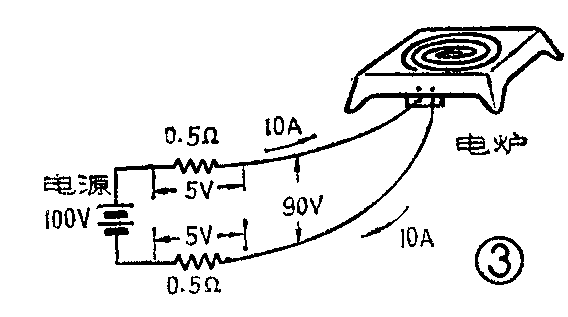
一条引线的电压降=0.5Ω×10A=5V
因为往返有两条引线,所以加在电炉上的实际电压,要比电源电压低2×5V=10V。
电阻的串联
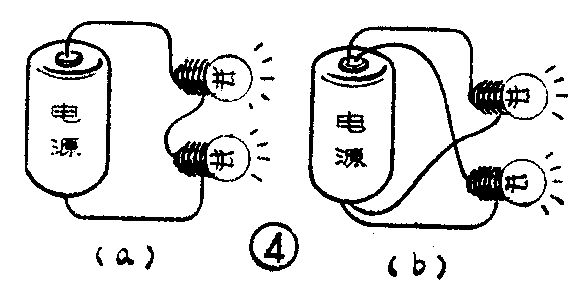
下面,我们再来看稍许复杂些的情况。如图4所示,假定负载是两个灯泡,这两个灯泡有两种可能的连接方式。从电源向外看去,如果将两个灯泡一个接一个地顺次连接起来,就叫做串联(图4a);如果将两个灯泡的一端连在一起,另一端也连在一起,象图4b的样子,就叫做并联。
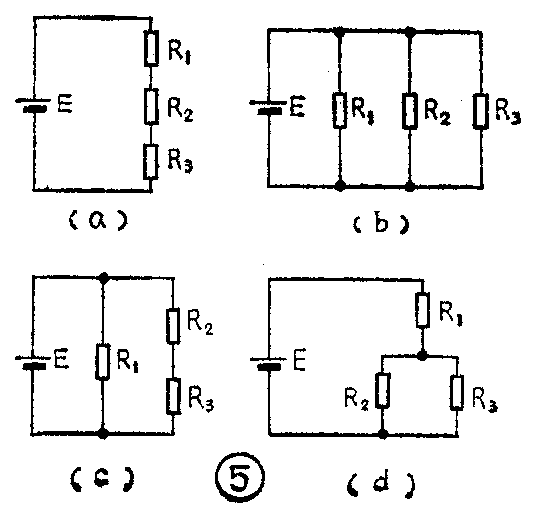
假如有三个电阻,就可能有图5所示的几种连接方式。图5a是一个电阻串联电路,图5b是电阻并联电路,图5c和d是串、并联的两种组合连接方式,叫电阻混联电路。在这一篇里,我们将先讲讲电阻的串联。图6画出了一个电源与两个串联电阻所组成的串联电路。在串联电路中,电流流通的路径上没有分岔,所以通过导线以及电阻R\(_{1}\)和R2的电流强度相等,都等于I。电阻的串联不仅限于两个或三个电阻,串联电阻的数目可以是任意的。在一个电路里无论有多少个电阻串联,通过每个电阻的电流都一定是相同的。但是根据欧姆定律,在同一电源的作用下,串联的电阻愈多,电流也就愈小。可见,在电路中串联电阻实际上为电流的流通设置了重重障碍。
串联电阻的分压
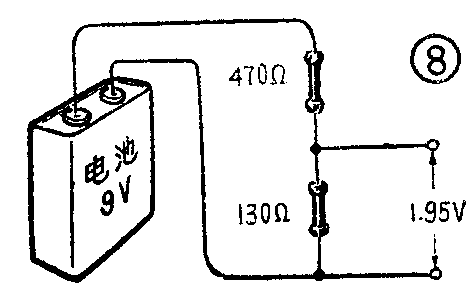
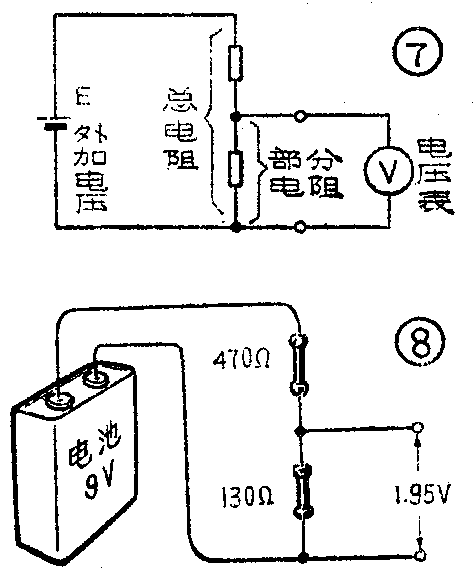
在电子电路中,串联电阻有一个重要的作用,就是构成一个简单的分压器。如图7所示,先把两个电阻串联起来,在串联电阻的两端加上一个电源电压E,然后将电压表跨接在其中任一个电阻的两端,量得的电压总要比电源电压低,这就是串联电阻的分压作用。所分出来的一部分电压与总电压(两个电阻上的电压之和)之比,叫做分压比。很容易证明,分压比也等于所取出电压的那部分电阻值与总电阻值之比。利用分压比,可以很方便地由总电压求出分电压。例如,在图8的电路中,将470Ω和130Ω两个电阻串联后接到9V电池上去,求得130Ω电阻两端的电压为9V×\(\frac{130Ω}{130Ω+470Ω}\)=1.95V 电压分配的比值1.95V;9V与电阻分配的比值\(\frac{130Ω}{600Ω}\)是相等的。这个比值就是分压比。
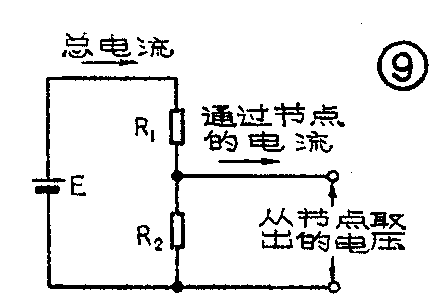
在实际应用中,常可利用串联电阻分压的原理,从一部分电阻上得到我们所需要的比较低的电压。但是在这种分压器中,负载是与分压电阻并联的,有一部分电流要流入负载支路(图9),只有当负载支路的电流很小时,分压效果才比较好。
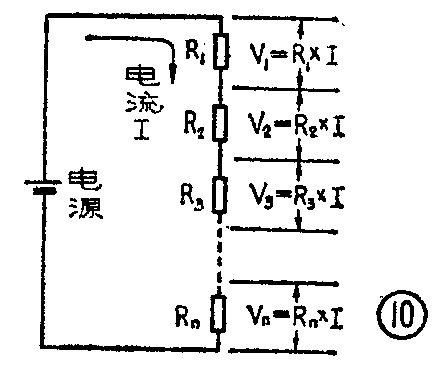
在图6所示的两个电阻串联电路的基础上,如果把串联电阻增加到n个(见图10),那么各个电阻上的电压将如何分配呢?下面我们用欧姆定律来进一步回答这个问题。在图10的电路中,当接通电源后,就有电流I从各个电阻通过。因为电阻是串联起来的,流过它们的电流都等于I。根据欧姆定律,电流I在各个电阻上产生的电压降分别为V\(_{1}\)=R1I,V\(_{2}\)=R2I,……V\(_{n}\)=RnI。
因为总电阻R=R\(_{1}\)+R2+……+R\(_{n}\)
总电压V=IR
=I(R\(_{1}\)+R2+……+R\(_{n}\))
=IR\(_{1}\)+IR2+……+IR\(_{n}\)
=V\(_{1}\)+V2+……+V\(_{n}\)
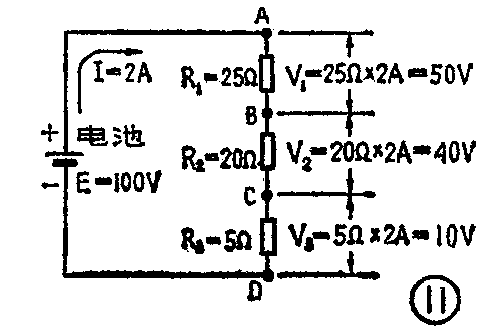
以图11所示的三个串联电阻R\(_{1}\)、R2、R\(_{3}\)为例。R1=25Ω,R\(_{2}\)=20Ω,R3=5Ω。把它们接在E=100V的电源上,流过电阻的电流为I=2A。可以求出各个电阻两端的电压。对于电阻R\(_{1}\)
V\(_{1}\)=25Ω×2A=50V
也就是电源电压有50V降落在电阻R\(_{1}\)上。同理,可以求得R2上的电压降V\(_{2}\)=20Ω×2A=40V, R3上的电压降V\(_{3}\)=5Ω×2A=10V。把各个电阻上的电压降加起来,V1+V\(_{2}\)+V3=100V,刚好等于电源电压100V。
在n个电阻串联时,可以利用分压比方便地算出各个电阻上的电压降,即
V\(_{1}\)=ER1R\(_{1}\)+R2+……+R\(_{n}\)
V\(_{2}\)=ER2R\(_{1}\)+R2+……+R\(_{n}\)
V\(_{n}\)=E
电压降的方向
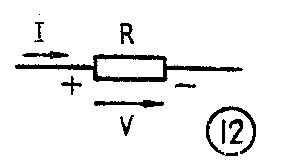
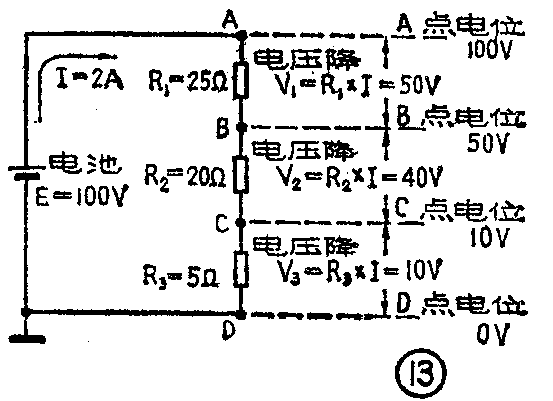
对于电阻本身来说,它的两端并没有正负之分。但是当有电流通过电阻时,就会产生电压降,从电位高的一端到电位低的一端的指向就是电压降的正方向(图12)。电压降的正方向是和通过电阻的电流的正方向相一致的,也就是由高电位至低电位的指向是顺着电流的方向。我们再举一个例子,见图13,图中电阻R\(_{1}\)的一端A点接电池正极,以地为参考点,A点的电位就是+100V。电流从A点流向B点,产生电压降R1×I,所以B点的电位低于A点,B点的电位是E-R\(_{1}\)I=100V-(25Ω×2A)=50V。同理,C点的电位是E-R1I-R\(_{2}\)I= 10V,D点的电位是E-RlI-R\(_{2}\)I-R3I=0V。从另一方面来看,电阻R\(_{3}\)的D点接地,可见D点的电位的确为0V。顺着电流的方向,电位从A点的100V下降到D点的0V。(张学志 颜超 宋东生编译)