人们所熟知的收音机等接收机是采用可变电容器来调谐的。但是随着科学技术的发展,对接收设备提出了越来越高的要求,特别是要求小型、轻便、可靠。采用空气或介质可变电容器作调谐,体积大而笨重,而且需要精密的齿轮和传动机构,就显得不适用了。然而采用变容二极管来代替机械可变电容器,使这个问题有了崭新的解决办法。这种调谐器称为电子式调谐器。
电子调谐元件——变容二极管小如半粒绿豆,重量轻,强度高,寿命长,转换快,能防尘防潮,抗冲击震动,受温度的影响极小。其工作原理是靠改变施加于变容管两端的反向电压,来达到改变管子结电容的目的。而变容二极管又接在调谐回路里,因此控制所加的直流电压,便可达到改变频率的目的。其调谐范围可达一个倍频程以上。此调谐电压多从一个电位器上取得,所需功率极小,特别是它可放在任意可以连线的地方,因此机械结构非常简单,制造维修都极为方便。尤其适于遥控和精密调谐,调谐精度为机械调谐所不及。
电子调谐是一项新技术,越来越得到广泛应用。美国研制的AN/PRC-70双波段电台、超高频地空电台AN/PRC-660T等均采用了这种电子调谐技术。其他如民用彩色电视机、黑白电视机、调频调谐器、调频收音机等也相继大量采用,近来在西欧发展尤快。在此基础上进一步提高,并派生出一些附加设备,诸如:按掣式预选器、触摸式选台、遥控选台,以至自动搜索调谐,数字显示技术等,使接收机更加趋于理想。
本文想简要地对变容管及电子调谐在调频收音机上的应用加以介绍,并谈谈电子调谐国内外的发展动向。
一、变容二极管
1.工作原理:变容二极管的外形和普通的开关二极管或检波二极管没有什么大的差别。在无线电电路里,不同的国家用不同符号来表示,题图画出了几个国家的画法供参考,第一、三是美国画法;第二、四分别为西德和西欧画法。
变容二极管为反向偏置二极管,它工作在雪崩击穿电压与小于接触电位之间的区域内,因此器件既不会击穿,也不会正向导电。倘若在变容二极管两端加上反向偏压U\(_{d}\)时(见题图),在PN结间便形成了一个既无电子又无空穴的区域——阻挡层。当外加电压Ud改变时,其阻挡层的宽度W也随之改变,进而我们把P、N两极看成是一平板电容器的两极板,阻挡层W为两极板间的距离。当反向偏压加大时,阻挡层W变宽,二极管呈现的电容就减小,反之则加大。于是可以说:变容管是一种特殊的二极管,其容量大小是随着加到其上的反向电压而变化的,其典型特性如图1所示,曲线是非线性的。
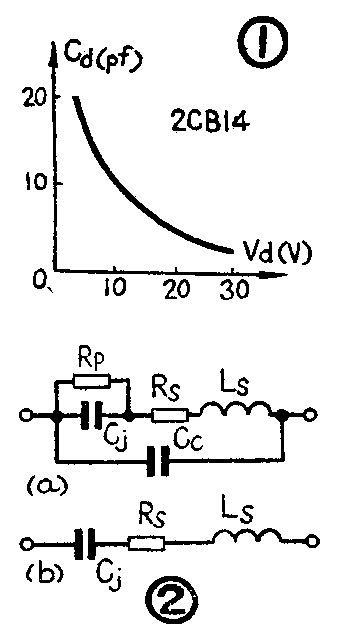
2.等效电路:变容二极管的等效电路如图2所示。其中C\(_{j}\)——可变的结电容;RS——串联电阻(包括接触电阻、引线电阻和体电阻);L\(_{S}\)——引线电感;RP——结的漏电阻;C\(_{C}\)——封装引入的杂散电容。图2(a)可简化成图4(b)。这几个参数随反向偏压改变而改变,参见图3。其中变容管的有效电容与所加偏压的关系为
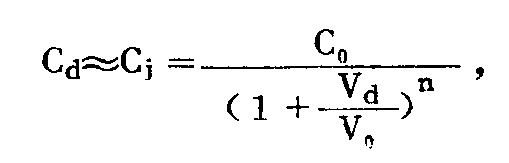
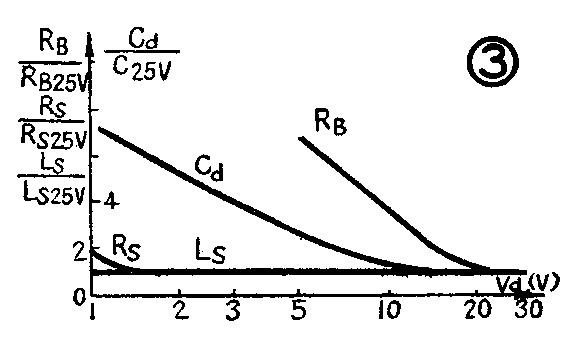
C\(_{d}\)是在加偏Vd时变容管的结电容;C\(_{o}\)为零偏压时的电容;Vd为跨接在变容管上的反向偏压;V\(_{o}\)为接触电位。对硅变容管来说,Vo=0.5~0.75伏;对砷化镓变容管V\(_{o}\)=1.1~1.2伏。n是由结的浓度梯度决定的常数。对线性缓变法n=1/3,突变结n=1/2,超突变结n=1~5。在高频应用时,n越大,Cd变化也越大,C\(_{d}\)~Vd曲线的斜率也越大。
3.变容管的主要参数:
击穿电压——当反向电压超过某一值时,变容管将产生雪崩击穿,这时的电压称为反向击穿电压BV\(_{d}\)。反向击穿电压的大小决定了变容管控制范围的上限,也决定了变容管的最小电容C最小。
结电容——由工作频率范围和选用的电感来确定。一般规定在反向电压为3伏和25伏时来检测变容管结电容的大小。对调频接收机和彩色电视机来说,C\(_{d}\)=20~3微微法左右;对调幅接收机Cd=(230~280)~13微微法左右。当然,反向偏压越小,结电容越大,变化也越剧烈,然而温度特性和互调性能也最差,因此反向偏压的下限一般取得不小于2伏。
电容比——变容管的结电容随所加偏压的变化,对电子调谐而言是一个重要参数。为扩大调谐范围,提高频率刻度线性,减少波段数,应选用较大变比的变容管。
据f=l/2π\(\sqrt{LC}\)和C\(_{d}\)=Co/(1+V\(_{d}\)/Vo)\(^{n}\)推导出:
f\(_{最高}\)/f最低=(V\(_{o}\)+Vd最大/V\(_{o}\)+Vd最小)\(\frac{n}{2}\)
上式决定了变容管的频率覆盖,从而就可确定应划分的波段数。对于n≈2的变容管,可望获得频率与V\(_{d}\)呈线性刻度。
Q值——变容管的效率表现为器件的品质因数Q,它反映了对谐振回路能量的吸收能力,其大小与串联损耗电阻R\(_{S}\)和非联损耗电阻RP有关。显然,其Q值不如空气可变电容器。尤其在高频、甚高频应用时,Q值将随频率和偏压而变化,是一复杂函数。图4、图5的曲线表明在甚高频应用时Q值的变化规律。
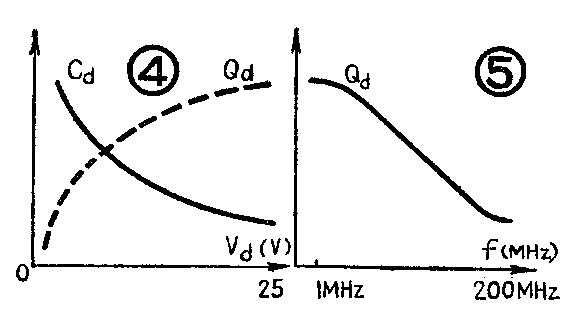
一般定义f\(_{T}\)=f工作、Q≈常数,国外较好的管子,当V\(_{d}\)=-3伏时,fT=30000兆赫;当V\(_{d}\)=-25伏时,fT=150000兆赫。(待续)(伟明)