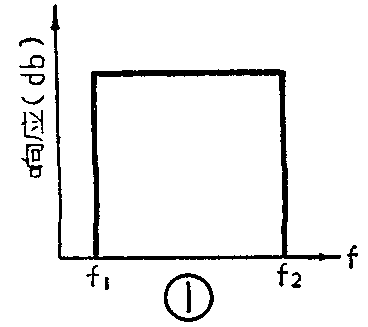
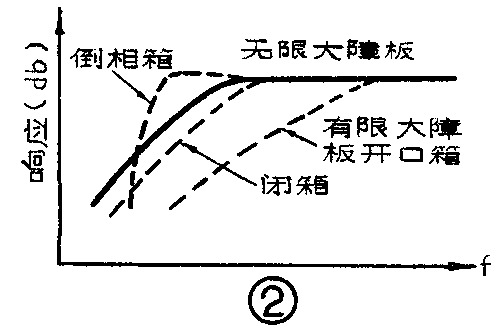
本文介绍的这个高保真箱式扬声器(扬声器连同扬声器箱的统称)的设计方法,是根据国外有关资料报导并结合我们的工作实践总结出来的。对高保真的箱式扬声器的要求是:在它所期望的频率范围内,能均匀重放扩音机输出的音频信号。图1是一个理想的频率特性,但实际特性一般只能做到象图2那样(图2中为同一扬声器在不同情况下测得的曲线)。可以看出,图2的低频特性还远不如图1好。利用我们介绍的这个方法来设计,在低频区域内能获得一条比较平坦的频响特性,并且原理清楚,设计计算简单方便。
设计基本原理
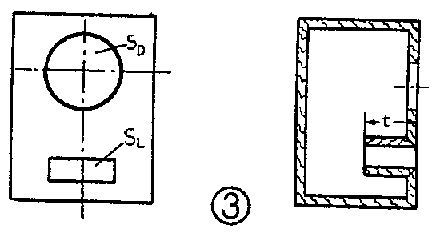
1.倒相式箱式扬声器 图3是倒相式扬声器的结构图。通过理论分析可得出,这种箱式扬声器在低频区域内其输出声压的相对响应可表示为:
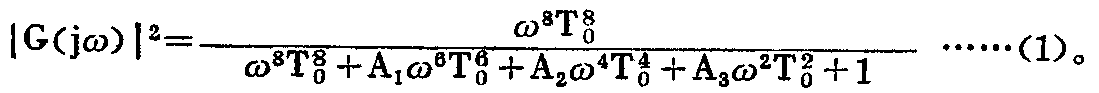
式中:T\(_{0}\)=(TBT\(_{S}\))\(\frac{^{1}}{2}\),TB=1;ωB,ωB=2πf\(_{B}\),fB为扬声器箱的谐振频率;T\(_{S}\)=1/ωS,ωS=2πfS,f\(_{S}\)为扬声器的谐振频率;A1\(_{2}\)3是由扬声器和其箱子的参数所决定的系数;ω=2πf,f为频率变量。
由(1)式可以看出,当T\(_{0}\)1\(_{2}\)3为特定值时,可以得到很多类型的频率响应曲线,其中有三种曲线在设计扬声器箱时十分有用。第一种是当A\(_{1}\)=A2=A\(_{3}\)=0时所得四阶巴特沃斯频率响应列线(称B4线),如图4。这是箱式扬声器能够得到的最佳平直特性曲线;第二种是取A\(_{1}\)2=\(_{3}\)\(\frac{^{1}}{2}\)=B(B可取大于零的实数值)时所得的响应曲线,3特性曲线(注意:如果B=0,\(_{3}\)线就变成B4线了);第三种是A\(_{1}\)2\(_{3}\)都不为零,而是随着某个参数K而变化的一些数值,此时所得的特性就是所谓的契比雪夫等波纹列线,又称C4线(对C\(_{4}\)线讲,0<K<1),它和最佳平直特性相比,其特点是在通带内有等值起伏的波纹。图4中的横坐标是按B4线的T\(_{0}\)标的。
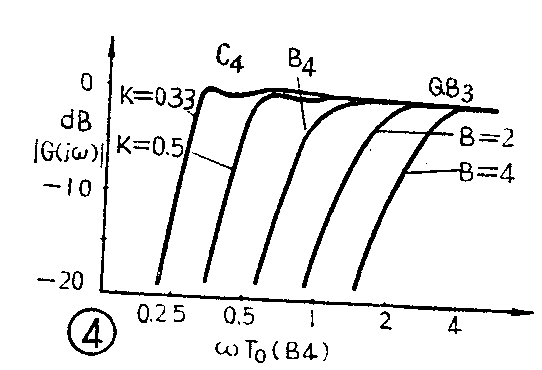
因为T\(_{0}\)1\(_{2}\)3这几个系数由扬声器和箱式扬声器的参数所决定,所以一旦响应曲线给定,即T\(_{0}\)1\(_{2}\)3为某一特定值时,就可以反过来找出扬声器和箱式扬声器之间的关系。根据国外有关资料报导,就B\(_{4}\)线、C4线和QB\(_{3}\)线来讲,扬声器和箱式扬声器参数之间在几个不同QL值时的关系如图5~图8所示。图中,f\(_{3}\)为倒相式扬声器的低频截止频率;h=fB/f\(_{S}\)为倒相式扬声器的调整比;α=CAS/C\(_{AB}\)为扬声器的声顺与箱体提供的声顺之比;QT为箱式扬声器(扬声器加助音箱)总的等效Q值,当扩大器的内阻为零时,则Q\(_{T}\)=QTS(Q\(_{TS}\)为扬声器本身的等效Q值);QL为考虑箱子的损耗引出的一个参量,一般取5~10(可以通过实验求得)。如果认为箱子是无损耗的,则Q\(_{L}\)→∞。
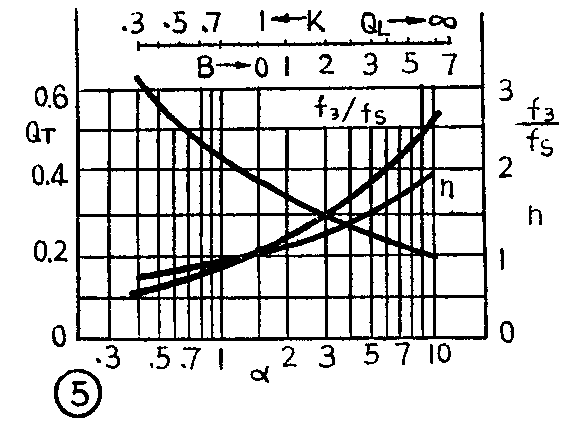
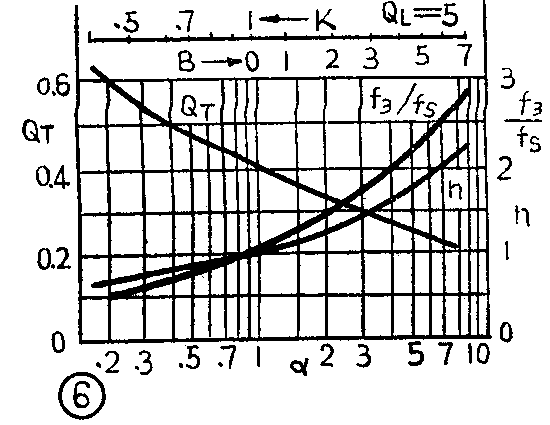
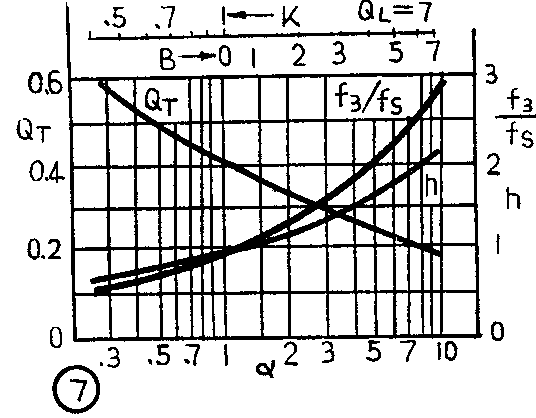
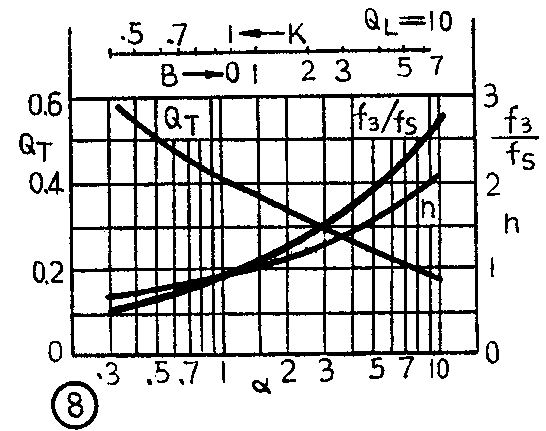
根据图5~图8这些曲线,再配合有关公式,就能很方便地设计一个倒相式扬声器。
2.密闭箱扬声器 密闭式扬声器箱在低频区域内的声压输出相对频率响应可表示为:
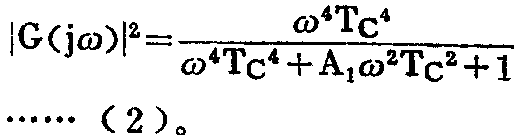
式中,A\(_{1}\)=a1\(^{2}\)-2,a\(_{1}\)=1/QTC,Q\(_{TC}\)为闭箱扬声器在谐振频率fC时的总的等效Q值;T\(_{C}\)=\(\frac{1}{2πf}\)C。
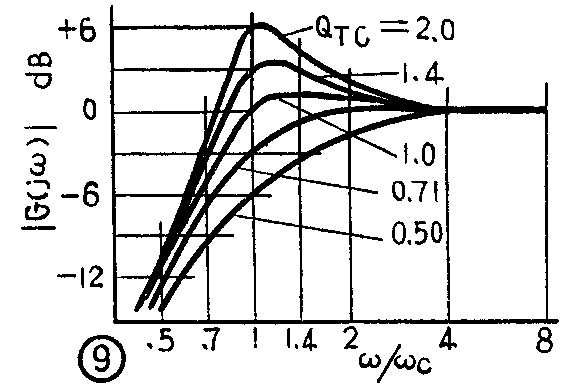
从(2)式可以看出,通过改变Q\(_{TC}\)的数值,可以得到如图9所示的一些很有用处的频率响应曲线,其中QTC=0.71时所得的响应最平坦,因此在设计时常常采用这一条曲线。
此外,密闭式扬声器与其扬声器单元的参数之间还有下列近似关系:
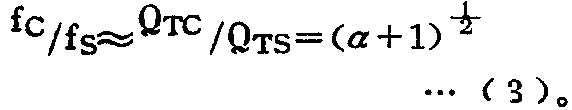
式中,f\(_{S}\)为扬声器的谐振频率;QTS为扬声器的等效Q值;α=C\(_{AS}\)/CAB为扬声器声顺与箱体提供的声顺之比。
根据所期求的响应曲线和(3)式的近似关系,可以比较容易地得到有关密闭箱扬声器的设计方法。
扬声器基本参数的测量
从前面的一些分析我们看到,要设计一个箱式扬声器,必须首先知道所用扬声器的一些基本参数,而这些参数对于业余制作的同志来说往往是不知道的,因此在设计以前还必须学会测量这些参数的方法。下面就讲讲这些问题。
①机械力顺C\(_{MS}\):用两根直尺,一根横搁在仰放的扬声器支架边缘上,另一根(无磁性的物质)垂直地显出扬声器膜片中央某点在横尺下的距离;然后,在扬声器膜片中央放一无磁性的重质M′(克),再测出此时的垂直距离,两次相减可得膜片因重量下沉的距离h(厘米),则扬声器的机械力顺为CMS=h/M′·g(g为重力加速度,其数值为981厘米/秒\(^{2}\))。在测量过程中,粘音圈的圆周应比较坚固,避免同膜片的其它地方相碰,否则易造成损坏。无磁性重质M′,一般取扬声器振动系统机械质量的80%~100%,不宜取太大,太大了会损坏扬声器并影响测量精度。例如,测试12英寸的扬声器时可附加16~20克。
②自由谐振频率f\(_{S}\):如图10所示,用一音频振荡器(输出阻抗要比音圈的电阻大10倍以上)接到音圈上,同时并联一只万用表。测量时,扬声器的辐射面离开反射物应在100厘米以上。调节振荡输出,就可以测得音圈两端电压。然后,改变振荡器的频率,使音圈振动幅度最大(此时万用表读数最大),这时的频率就是扬声器的自由谐振频率fS,增加或降低频率,使读数下降3分贝(即万用表读数下降到最大读数时的70%),两个频率之差Δf就是带宽,于是就可得出扬声器的机械品质因数Q\(_{M}\)=fS/Δf。
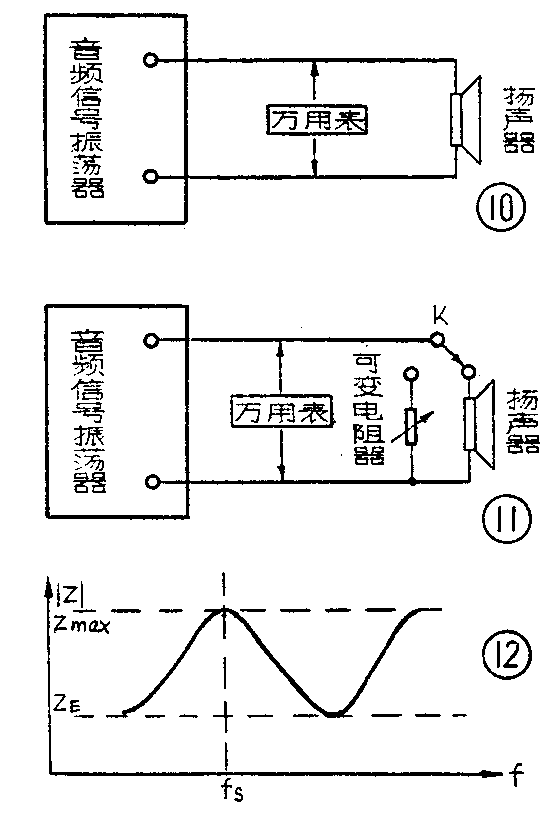
③阻抗Z及其特性的测量:如图11所示,当开关K分别接到扬声器和无感可变电阻器时,调节电阻器保持两者电压相等,此时电阻器上的电阻值(可以用万用表测量)即是扬声器的阻抗值。如果连续改变振荡器频率,重复上述测量,可以绘出如图12所示的扬声器的阻抗特性曲线。图中Z\(_{max}\)为扬声器阻抗最大值,ZE为扬声器阻抗最小值。
④音圈直流电阻R\(_{E}\):(可用万用表直接测量。)
⑤计算Q\(_{TS}\)、M和RM:扬声器的等效品质因数Q\(_{TS}\)≈QM·Z\(_{E}\)/Zmax;振动系统的等效质量M=1/4π\(^{2}\)f\(_{S}\)2CMS(克);振动系统的力阻R\(_{M}\)=2πfSM/Q\(_{M}\)〔达因·秒\(^{2}\)/厘米〕。
根据实验,这些参量的典型值为:C\(_{MS}\)为(3~5)×10\(^{-7}\)(厘米/达因);fS为20~100赫;Q\(_{M}\)为3~5;QT≈Q\(_{TS}\),约为0.2~0.5;大扬声器M一般为40~60克,小扬声器M一般为10~20克。(待续)(潘雨洲 江敦春)