OTL电路的分析与设计（续）

严格地说，图1电路中推挽两管的输入信号并不完全相等，因为两管输入信号并不取自推动管BG\(_{1}\)集电极负载的同一点，而是将BG3管基极b\(_{3}\)接到R4下端，将BG\(_{2}\)管基极b2接到R\(_{4}\)上端。因而从对称输入着眼，R4也不能很大，必须使R\(_{4}\)《R3，做到两推挽管输入信号尽量相等。

BG\(_{1}\)管集电极电阻R3通过负载R\(_{L}\)接到电源负端，是为了构成电压正反馈，以提高功率。在静态时，低阻的RL和R\(_{4}\)远小于R3，故BG\(_{1}\)管的直流负载主要是R3。在动态时，C\(_{3}\)相当于短路，R3等效跨接在BG\(_{2}\)管的b、e间（若忽略R4，R\(_{3}\)也可看作等效跨接在BG3管的b、 e 间），如图6所示。当A点有信号输出时，总是被R\(_{3}\)、R4和BG\(_{1}\)管的内阻分压，馈给BG2、BG\(_{3}\)的基极，显然，通过R3反馈到推挽两管基极的信号的极性是与A点输出信号相同的，因而属于电压正反馈，其作用是使输出级的功率增益得到提高。但这种正反馈对放大器的频响不利。负反馈有利于展宽放大器的频响，正反馈却要压缩频响，尤其是对低端频响影响更为严重。因此R\(_{3}\)的大小要适当控制，因为正反馈量的大小主要取决于R3。

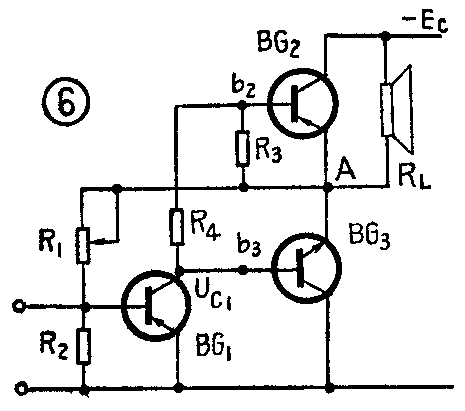
2.图解分析和计算：同变压器耦合推挽功放一样，我们也可将推挽管的两组输出特性曲线相互倒置，如图7所示，用作图的方法来分析辅助对称OTL电路。

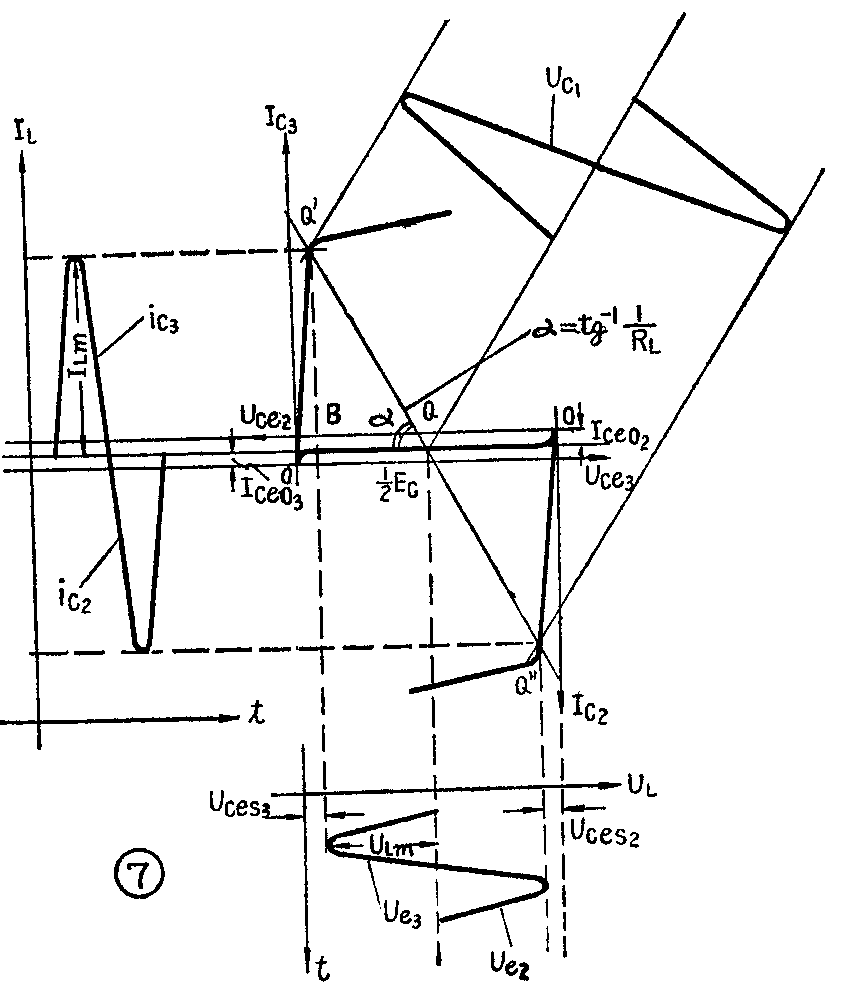
因为两管工作在乙类状态，I\(_{ceo2}\)=Iceo3=I\(_{ceo}\)，故两组曲线应在Ic＝I\(_{ceo}\)处重叠，静态工作点Q就在Ic＝I\(_{ceo}\)、Uce=-E\(_{c}\)／2处。过Q点作斜率为tgα=1/RL的交流负载线。当推挽两管输入信号为U\(_{c1}\)时，随Uc1变化， 工作点Q就沿交流负载线在Q′-Q″点间滑动。于是可作出相应的输出电流I\(_{L}\)、输出电压UL的波形。图7采用习惯上的共e电路的作图法。因而作出的U\(_{L}\)与Uc1倒了相。在共c电路的情况下，U\(_{L}\)波形正好与Uc1同相，因而与图7所示相反。但对共c电路和共e电路来说，其输出特性的不同仅在纵坐标标志的意义不同，前者表示I\(_{e}\)，后者表示Ic，而在量值上I\(_{e}\)≈Ic，因此图7作法并不影响我们进行分析、计算。

由于发射极电阻R\(_{6}\)=R7=R\(_{e}\)（参看上期本文图1），它们对直流工作点的稳定有好处，但在放大器交流工作状态下都是与负载RL串联的，也是交流负载的一部分，它们上面要消耗一些功率。在R\(_{e}\)与RL相比不能忽略时，交流负载应考虑为R\(_{e}\)+RL，故负载线斜率应算作tgα=1/（R\(_{e}\)＋RL）。

下面结合图解分析介绍几项参数的计算方法。

①输出功率P——只要两管选得对称，输出电流、电压的波形也会对称。在量值上i\(_{c2}\)=ic3，U\(_{e2}\)=Ue3若忽略穿透电流I\(_{ceo}\)，可认为负载电流幅值ILm与管子集电极电流幅值I\(_{cm}\)近似相等，即ILm≈I\(_{cm}\)。若再忽略饱和压降Uces，且不计R\(_{e}\)，又可认为负载电压幅值ULm与管子发射极电压幅值U\(_{em}\)近似相等，即ULm≈U\(_{em}\)=Ec／2。从图7所示三角形△QBQ′可写出关系式

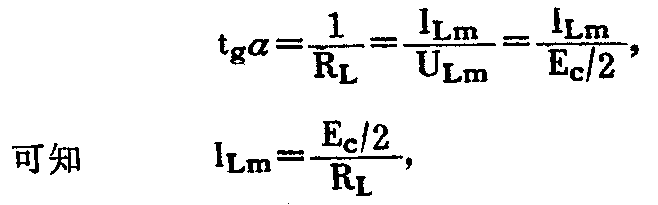
输出功率P按有效值I\(_{L}\) UL计算，可算得

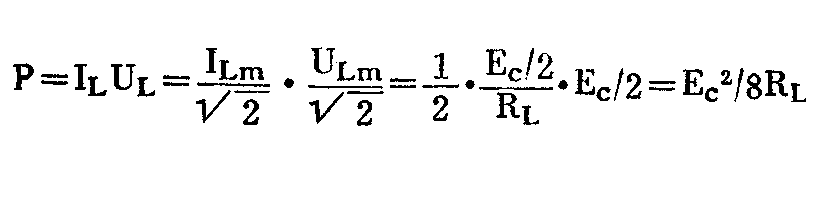
式中：E\(_{c}\)的单位为伏；RL的单位为欧；输出功率P的单位为瓦。

例如，E\(_{c}\)=6伏，RL= 8欧，则最大不失真输出功率为：

如果饱和压降U\(_{ces}\)不能忽略，从图7可以看出，幅值ULm=E\(_{c}\)/2-Uces=（E\(_{c}\)-2Uces)/2，则

上式说明，R\(_{e}\)越大，损耗在Re上的功率越多，输出功率就越小。因此R\(_{e}\)的确定不但要考虑到放大器的稳定性，还必须考虑到不致过多地损失功率，一般总选Re≤R\(_{L}\)/10。

从图7还可看出，输出功率（P=I\(_{Lm}\)ULm/2）正好等于三角形△QBQ′的面积，要提高输出功率，就要设法加大△QBQ′的面积。在负载R\(_{L}\)已定的情况下，交流负载线斜率tgα=1/RL已定，要加大△QBQ′，只有提高电源电压E\(_{c}\)。这样将使负载线向右平移，使交点Q′、Q″上升，集电极电流Ic就急剧增大。或者在E\(_{c}\)已定的情况下，要想加大△QBQ′面积，只有减小RL（选用低阻负载），使负载线更陡，交点Q′、Q″也上升，集电极I\(_{c}\)也将急剧增大。无论哪种情况，都要增大Ic，故这种功放电路对功率管的最大集电极电流参数I\(_{CM}\)要求很高。

②效率η——要计算效率，先要计算电源消耗功率，即电源在一周期内供给放大器的能量。对正弦波来说，不能直接计算一个周期的平均值，因为两个半波等值反相，其平均值恰好为零，但可先计算出半个周期内的平均值，再推算一个周期内的平均值。经计算可知，电源在有功率输出的一个周期内，供给（或消耗）在输出管的电流平均值为I-\(_{c}\)=2Icm/π。前已提过，幅值I\(_{cm}\)≈ILm=（E\(_{c}\)－2Uces)/2R\(_{L}\)，每个管的供电电压为Ec/2，于是可算出电源消耗功率为

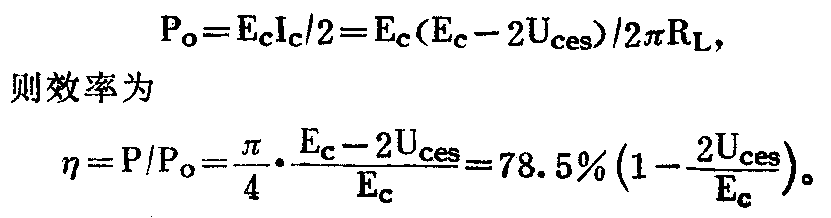
上式说明，若管子的饱和压降U\(_{ces}\)小到可以忽略，放大器的理想效率同变压器乙类推挽放大器一样可以达到78.5％。

③管子最大集电极损耗功率P\(_{cm}\)——电源供给放大器的直流功率大部转换成交流功率输出，剩下的消耗在管子集电极，使管子发热。因而可以认为，推挽管的最大集电极管耗为电源总消耗功率与输出功率之差，即Pcm= P\(_{o}\)－ P。为计算方便，先将Po公式简化为

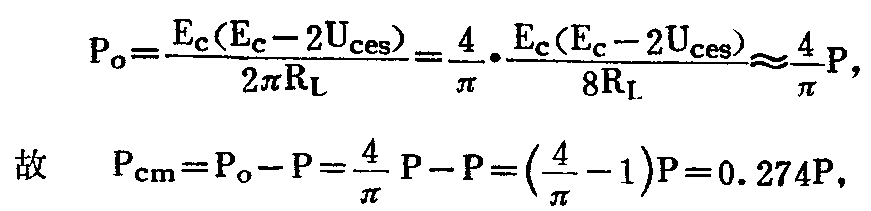
则每管的集电极功耗仅为P\(_{cm}\)/2=0.137P。

需要说明：上述结果都是在最大动态范围（即输出最大不失真功率）情况下得出的。但实际上管子并非工作在动态范围最大的情况下，即电流、电压并未充分利用，因而实际管耗要加大。实验证明，当电流电压利用系数k=0.636时，两管管耗最大为P\(_{cm}\)=0.406P。另外，上述结果都是在正弦信号的条件下得出的，实际上放大器输入信号并非单一正弦信号，而是一个很复杂的非正弦信号（例如语言、音乐等），因此管耗也要加大。考虑到这两个情况，每个推挽管的最大管耗应按0.25P考虑。例如，若要求输出功率P=1瓦，则每个推挽管的最大集电极功耗必须满足PCM≥0.25P=0.25瓦。

④推挽管的选择——归纳上述情况，便可得到选择推挽管的三个主要条件，即：

最大反向击穿电压BV\(_{ceo}\)≥Ec；

最大集电极电流I\(_{CM}\)≥Icm=（E\(_{c}\)-2Uces)/2（R\(_{L}\)+Re）；

最大集电极功耗P\(_{CM}\)≥0.25P。

此外，从图7曲线可知，还要求推换两管的两组特性曲线应尽量一致，输出波形失真才最小，但不易办到。在两管配对时，特别要注意两管在I\(_{CM}\)时的β和饱和压降Uces，即图7中Q′点和Q″点的β值、U\(_{ces}\)应尽量一致，Uces越小越好。

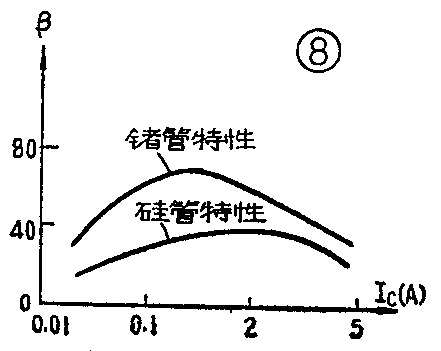
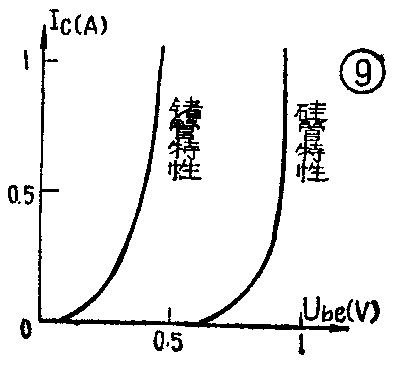
3．对称性：前已提到，图1电路中推挽管只有用同一材料的管子组成时，对称性才能基本得到保证。从图8所示大功率管的β—I\(_{c}\)特性曲线可以看到，锗管与硅管的特性不一致，锗管的β值随Ic增大而急剧上升，到一定值后缓慢下降，而硅管β值却随I\(_{c}\)增大而缓慢上升，到一定值就急剧下降。这就说明，尽管在静态时可以挑选两管β值一致，但在动态时两管β值的变化是不一致的。另外，从图9晶体管的Ube—I\(_{c}\)转移特性曲线又可看到，硅管的特性曲线比锗管要陡，即在动态时，对应于同一输入信号变化△Ube，其输出电流变化△I\(_{c}\)不一样。还有硅管与锗管的温度特性差别也较大。这些因素都将导致输出波形失真。而目前硅PNP型和锗NPN型大功率管还很少见，不可能用相同材料不同导电极性的大功率管组成推挽电路，因此要采用下一节介绍的复合管电路。

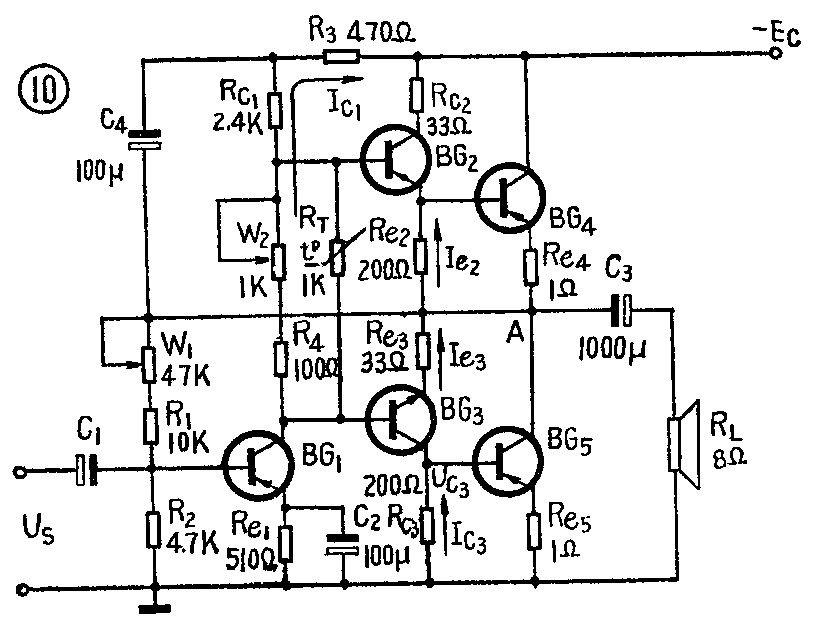
这种电路如图10所示。它采用同材料、同极性的大功率管，并配用中功率或小功率的同材料、不同极性的管子组成复合推挽电路，其特点为：

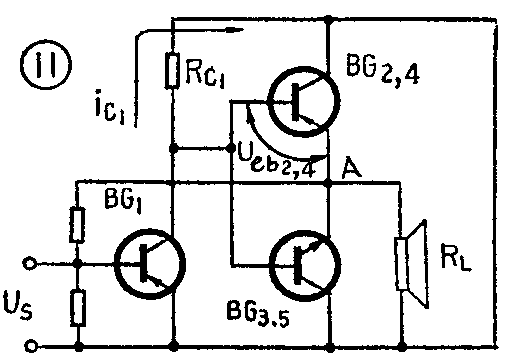
1．复合管：两个管子复合可看成一个管子。图10电路的交流工作状态可简化成图11所示。推挽管BG\(_{2、4}\)和BG3、5仍然工作在共c状态，故仍具有共c电路的一切特点。电路的分析、计算方法同前。

2．对称性：为了对称，要求β\(_{2}\)·β4=β\(_{3}\)·β5，并不要求复合两管的β值相等，但也不能相差太多，例如β\(_{4}\)=5，β5=40，相应地β\(_{2}\)=80，β3=10，这样虽然β\(_{2}\)β4=β\(_{3}\)β5=400，但不合要求，因为若输出电流I\(_{c4max}\)= 1安，则Ib4max=1/5=0.2安=I\(_{e2max}\)。这对中功率管来说，其工作点已进入饱和区，信号将严重失真。

为了对称，推挽两臂各管的饱和压降U\(_{ces}\)应选得较为一致，且越小越好。希望BG2、BG\(_{3}\)两管采用同一材料、不同导电极性的管子。

复合管也有缺点，从关系式I\(_{c}\)≈β2β\(_{4}\)Ib2可以推断：复合管BG\(_{2、4}\)的穿透电流也会有Iceo≈β\(_{2}\)β4I\(_{cbo2}\)这个关系，即其穿透电流也是大幅度增长的。因而复合管的温度稳定性总不如单管好。为了克服这一缺点，图10电路中，在输出管BG4、 BG\(_{5}\)基极相应接入偏置电阻Re2、R\(_{c3}\)。当调整电位器W2确定静态电流I\(_{c3}\)（≈Ie3＝I\(_{e2}\)）时，就给输出管加上了一定的静态偏置电压Ie2R\(_{e2}\)、Ic3R\(_{c3}\)，使输出管BG4、BG\(_{5}\)（和BG2、BG\(_{3}\)）均工作在甲乙类，即都建立一定的静态电流Ico，而I\(_{co}\)远大于Iceo，所以由于温度变化引起的I\(_{ceo}\)的变化，对静态电流工作点的影响就可忽略，从而提高了温度稳定性。但是Re2、R\(_{c3}\)接入后，对注入输出管的信号也有分流作用，因而电路增益会受到损失。此外， Re2、R\(_{c3}\)。接入后， BG2与BG\(_{3}\)管电路的结构并不一样，BG2管信号从其发射极输出，电压增益K\(_{V2}\)≤1；BG3管则从集电极输出，其电压增益K\(_{V3}\)＞1，若不采取措施，使KV3≈1，就会使输出不对称，造成严重失真。

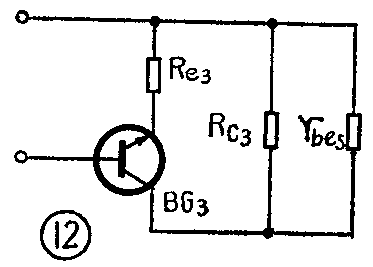
怎样才能使K\(_{V3}\)≈1呢？我们将BG3管交流工作电路简化成图12，其中BG\(_{3}\)管的等效输入电阻为rbe3，BG\(_{5}\)管的等效输入电阻为rbe5（作为BG\(_{3}\)管的交流负载）。经分析可知，在电流串联负反馈放大器中，只要反馈电阻Re3足够大，满足β\(_{3}\)Re3》r\(_{be3}\)，则放大器增益可近似为KV3≈R′\(_{c3}\)/Re3。式中R′\(_{c3}\)为集电极交流负载，即R′c3=R\(_{c3}\)‖rbe5（‖表示两电阻并联）。这说明在负反馈较强的情况下，放大器的增益几乎与管子无关，仅决定于放大器交流负载与反馈电阻之比。如果使R′\(_{c3}\)=Re3，就可做到K\(_{V3}\)≈1。用这样的方法来计算电路，就可使BG2、BG\(_{3}\)两管的增益都接近于1，即KV2=K\(_{V3}\)≈1，推挽两臂能对称地工作。

3．自举电路：图10电路由R\(_{3}\)、C4构成所谓自举电路。先假定没有R\(_{3}\)、C4，则图10电路的交流工作状态如图11所示。由于i\(_{c1}\)流经Rc1要产生压降i\(_{c1}\)Rc1，故当BG\(_{2、4}\)导通时， A点电位向负端摆动不到-Ec，而只能达到U\(_{A}\)=-（Ec-i\(_{c1}\)Rc1-U\(_{be2、4}\)），式中Ube2、4=U\(_{be4}\)＋Ube2。也就是说， BG\(_{2、4}\)管不能充分导通，输出功率受到限制。

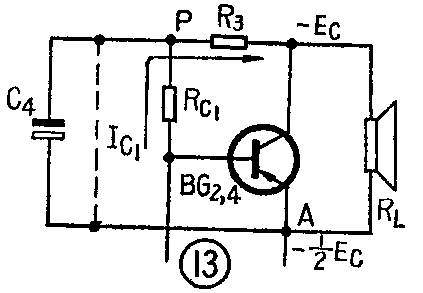
当接入R\(_{3}\)、C4后，如简图13所示。在静态时，R\(_{3}\)与Rc1、R\(_{4}\)等一起构成BG1管集电极负载。这时P点的直流电位为U\(_{P}\)=-(Ec－I\(_{c1}\)R3）。由于R\(_{3}\)较小，可近似认为UP≈-E\(_{c}\)，而中点电位UA=-E\(_{c}\)/2，故电容C4被充电，两端电压U\(_{c4}\)=Ec/2，极性是下端正上端负，因而也可认为P点电位是中点电位U\(_{A}\)叠加了电容上电压Uc4，即U\(_{P}\)=UA＋U\(_{c4}\)=－Ec。

在动态时，若BG\(_{2、4}\)管饱和导通，中点电位向电源负端摆动，即UA→-E\(_{c}\)，相应地P点电位将为：UP→（U\(_{A}\)+Uc4)＝－（E\(_{c}\)+Ec/2）＝－3E\(_{c}\)/2，即由于C4的作用，将P点电位举高了，相当于在P点接了个高压电源一样，举高的电压足以抵消R\(_{c1}\)上的电压损失，使A点电位能摆动到-Ec，确保电源电压得到充分利用，输出功率达到最大值。这里R\(_{3}\)的作用显然是为了将P点与电源-Ec隔开，防止电源的低内阻将C\(_{4}\)上电压钳位到电源电压，以利于P点电位升高（向负端）。为了使自举电路不致过多地影响放大器频响，电容C4的容量必须足够大，一般以最低频率f\(_{1}\)进行估算，即C4≥1/2πf\(_{1}\)R3。

已知喇叭阻抗R\(_{L}\)=8欧，试设计一输出功率P=5瓦、f1=50赫的功放电路。

1．电路选择:根据要求应选用复合管OTL电路。

2．确定电源电压：根据P=E\(_{c}\)\(^{2}\)/8RL,可知E\(_{c}\)=\(\sqrt{8R}\)LP=8×8×5=17.8伏。考虑到管子饱和压降U\(_{ces}\)和发射极电阻Re，电源电压应有足够余量，以满足P=（E\(_{c}\)－2Uces）2/8（R\(_{L}\)+Re），一般留20％的余量已可，即实际电源电压应为

考虑到电源电压系列，取E\(_{c}\)＝24伏。

3．输出管BG\(_{4}\)、BG5的选择：根据选择推挽管的三个主要条件可知：BV\(_{ceo}\)≥Ec=24伏；I\(_{CM}\)≥Icm=E\(_{c}\)/2RL=24/2×8=1.5安；P\(_{CM}\)≥Pcm=0.25P′＋E\(_{c}\)ICQ/2，其中I\(_{CQ}\)是推挽管工作在甲乙类的静态电流，大功率管一般取ICQ=20毫安。P′为实际输出功率，即P′=E\(^{2}\)\(_{c}\)/8RL=242/8×8=9瓦，故P\(_{cm}\)=0.25×9＋0.5×24×0.02=2.5瓦。

选用3AD6C可满足要求，其指标为：BV\(_{ceo}\)=30伏；ICM=2安；P\(_{CM}\)＝10瓦（加120×120×4mm\(^{3}\)散热片）

4．R\(_{e5}\)、Re4的选取：一般取R\(_{e4}\)=Re5=R\(_{e}\)=RL/10，故选取R\(_{e4}\)＝Re5=0.5～1欧。

5．复合管选择：根据图8可知，动态时晶体管β值随I\(_{c}\)上升而增大。前已算得ICQ～I\(_{cm}\)=20毫安～1.5安，若BG4、BG\(_{5}\)相应的β值变化范围为β4=β\(_{5}\)=20～100，故可算得基极电流的动态范围为

由复合管原理可知，这一基极电流相应地由BG\(_{2}\)、BG3管提供，故要求两管最大集电极电流应满足I\(_{CM2}\)=ICM3≥I\(_{b4}\)=Ib5=15毫安。两管最大集电极反压同输出管一样仍要满足BV\(_{ceo}\)≥Ec。最大集电极功耗的计算同输出管是一样的，因为BG\(_{2}\)、BG3也是工作在甲乙类的。为简便起见，也可从输出管推算过来。前面已算过输出管的最大集电极功耗为P\(_{cm4}\)=Pcm5＝P\(_{cm}\)＝2.5瓦。按输出管最低β值进行估算（这时管耗最大），则可知Pcm2=P\(_{cm3}\)≥Pcm4/β\(_{4}\)=2.5/20＝125毫瓦。

根据上述计算结果查手册，BG\(_{2}\)管可采用3AX31C，BG3管可采用3BX1E。两管指标均满足P\(_{cm}\)≥125毫瓦， Icm≥15毫安， BV\(_{ceo}\)≥24伏的要求。

6．R\(_{c3}\)、Re2的确定：R\(_{c3}\)、Re2分别提供输出管BG\(_{5}\)、BG4的静态偏流，同时也对信号分流，故不宜取得过小，一般按输出管的输入电阻r\(_{be5}\)（＝rbe4）来进行估算，即取R\(_{c3}\)=Re2=（1～10）r\(_{be5}\)。3AD6C的输入电阻约数十欧姆。这里若估为rbe5=r\(_{be4}\)=40欧，则可取Rc3＝R\(_{e2}\)=5rbe5=5×40=200欧。

7．R\(_{e3}\)、 Rc2的确定：由于BG\(_{3}\)工作在倒相放大状态，要使得KV3=K\(_{V2}\)≈1，必须使Re3＝R′\(_{c3}\)。 R′c3是集电极交流负载，即R′c3＝R\(_{c3}\)‖rbe5＝（200×40）/（200＋40）＝33欧，因而可取R\(_{e3}\)＝Rc2=R′\(_{c3}\)=33欧。

8．BG\(_{2}\)、BG3 静态工作点的确定：从图10电路可算得BG\(_{3}\)管集电极电位Uc3＝I\(_{c3}\)Rc3＝I\(_{CQ5}\)Re5＋U\(_{be5}\)=0.02×1＋0.2=0.22伏，故其发射极静态电流Ie3=I\(_{c3}\)＋Ib5=U\(_{c3}\)/Rc3＋I\(_{CQ5}\)/β5=0.22/200+0.02/20≈2毫安=I\(_{e2}\)，即BG2、BG\(_{3}\)管静态电流应调到Ie3=I\(_{e2}\)=2毫安。这一电流可以调整两管基极偏压来确定。

若偏置电阻为R\(_{b}\)=（R4+W\(_{2}\)）‖RT，则偏压可表示为U\(_{Rb}\)=Ube3＋I\(_{e3}\)Re3＋I\(_{e2}\)Re2＋U\(_{be2}\)， BG3与BG\(_{2}\)均选用锗管，故发射结正向电压均估为Ube3=U\(_{be2}\)=0.2伏，又知Ie3=I\(_{e2}\)=2毫安，故可算得偏压URb＝0.2＋0.002（33＋200）＋0.2≈0.87伏。推动管BG\(_{1}\)总是工作在甲类的，可取Ic1=4毫安。这样就可算得偏置电阻R\(_{b}\)=URb／I\(_{c1}\)=0.87/0.004≈220欧，于是可选取热敏电阻RT＝1千欧，R\(_{4}\)＝100欧，W2＝1千欧。调整电位器W\(_{2}\)，可以很方便地控制偏压URb。

9．BG\(_{1}\)管静态工作的确定：由于中点A的静态电位为-Ec/2，故可认为I\(_{c1}\)流经Rc1和R\(_{3}\)产生的压降为U（Rc1+R\(_{3}\)）=Ec/2-I\(_{e2}\)Re2-U\(_{be2}\)，即

前已分析过，要求R\(_{c1}\)》R3，故按电阻系列，取R\(_{c1}\)＝2.4千欧，R3=470欧。取自举电容C\(_{4}\)=100微法，取Re1=510欧，C\(_{2}\)=100微法。偏置电阻取见R2=4.7千欧，R\(_{1}\)=10千欧，W1=47千欧。

10．输出电容C\(_{3}\)的确定：按公式计算

取C\(_{3}\)=1000微法/25伏，使频响低端有足够余量（一般总是取计算值的一倍以上）。（金国钧）