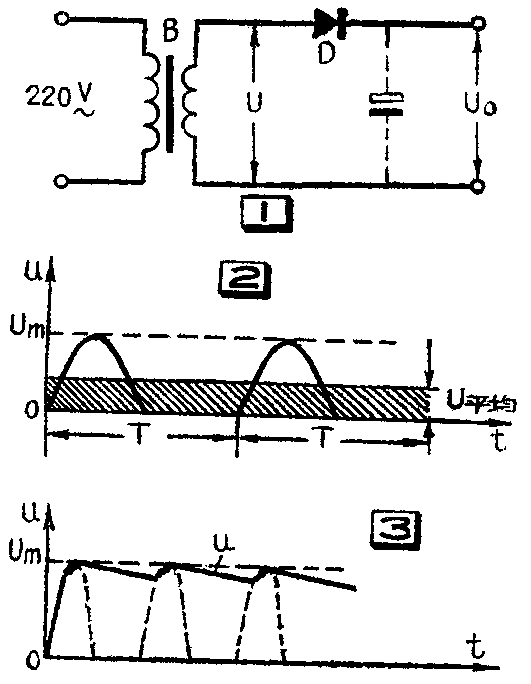
图1是一个简单的半波整流电路,如果我们用电表来测量一下它的输出电压,就会发现一个有趣的问题。
假使变压器B的次级交流电压U为6伏,在不接滤波电容器C的情况下,用直流电压表测得的整流输出电压U\(_{o}\)只有2.7伏;但是,当接上一个100微法的滤波电容以后,用同样的方法再去测量Uo时,电表的指数却是8.4伏了。这是为什么呢?
如果我们来熟悉一下下面所要谈的一些电工知识,这个问题也就不难理解了。
平时我们所说的交流电压,只要不加以特别说明,一般都是指的正弦交流电压。因此,以后凡是提到交流电压,就是指的正弦交流电压。
交流电压的瞬时值(用符号u表示)的大小和方向都是随时间而变化的。它的最大值叫做峰值或称振幅,有时干脆就叫做最大值(用符号U\(_{m}\)表示)。我们日常所说的380伏或220伏电压,既不是瞬时值,也不是最大值,而是指的交流电压的有效值(用符号U表示)。那么有效值又是什么意思呢?它是这样规定的:一个交流电与一个直流电分别加到阻值相等的电阻上,如果在交流电的一个周期内,两者所消耗的电能相等,这时我们就把这个直流电的数值,叫做交流电的有效值。理论和实践都可以证明,对于正弦交流电来说,有效值与最大值之间的关系是:
U\(_{m}\)=\(\sqrt{2}\)U≈1.4U。
现在我们再回头来讨论前面提出的问题。由于二极管的单向导电性,使得电路只有在变压器次级的上端为正半周时才导通,其输出电压波形是半个正弦波(如图2所示),这就是通常所说的半波整流波形。这时我们用直流电压表测得的输出电压,是这个半波整流波形的平均值。那么平均值又是什么呢?顾名思义,就是把波形平均一下的数值。更具体一点说,就是把一个周期内的瞬时值加起来,再被周期去除。理论上可以计算出这种半波整流波形的平均值与最大值之间的关系是:U\(_{平均}\)=Um/π。如果把最大值与有效值的关系代入此式,就可以得到平均值与有效值之间的关系:
U\(_{平均}\)=\(\sqrt{2}\)U/π。即:U平均=0.45U。
在前面的问题中,我们假定变压器次级电压为6伏,这是指的有效值,也就是:U=6伏。这样就可用上式求出:U\(_{平均}\)=0.45×6伏=2.7伏。这与我们测得的结果是相同的。
当接上滤波电容器之后,情况就不同了,如图3所示,在正半周时,二极管导通,电源通过二极管的低电阻(正向电阻)向电容器迅速充电,很快达到电压的最大值U\(_{m}\);负半周时,二极管截止,电容器充上的电压通过负载电阻放电,对于我们所讨论这个问题来讲,负载电阻就是直流电压表的内阻,通常它的阻值是很大的。因此,电容器放电进行得很缓慢,电容器C上的电压,也就是整流器的输出电压,降低得很慢,如图3中的曲线u。由于它放电很慢,刚刚放掉一点,下一个正半周又使电容器充电,因此只要电容器足够大电容器上的电压基本可以保持在Um的数值。于是,这时在整流器的输出端测得的直流电压,也即图3波形的平均值,它基本上等于或接近于输入交流电压的最大值。我们已经知道输入电压的有效值U=6伏,那么根据前面所讲的关系式就可以求出它的最大值:U\(_{m}\)=1.4×U=1.4×6伏=8.4伏。这与我们实际测量的结果也完全一致。(朱蔼初)