在功放电路中,人们常称输出级和扬声器间不用输出变压器耦合的电路为“无输出变压器电路”,简称OTL电路(英语OTL为 Output Transformerless)。又称推动级和输出级间不用输入变压器耦合的电路为“无输入变压器电路”,简称ITL电路。这类无变压器功放电路甩掉了级间耦合用的变压器,改用直接耦合。这样,电路结构虽然复杂些,但便于加负反馈电路,能使频响宽、失真小,易于满足大功率和小型化的要求。在立体声设备中,它是个相当重要的部分。
无变压器功放电路也是一种乙类单端推挽电路,但为了避免交越失真,实际上它总是工作在甲乙类状态。其电路形式若从信号倒相的方式来分,目前见到的约有五种:①辅助对称式(或称互补对称式)。这种电路采用两个对称的、不同导电极性的管子作推挽输出。②标准辅助对称式(或称复合互补对称式)。这种电路采用两个对称的、不同导电极性的复合管推挽输出。③输入变压器倒相式。这种电路用输入变压器进行信号倒相,故可用两个对称的、相同导电极性的管子推挽输出。④c-e倒相式。这种电路由推动级管子的集电极和发射极对称地输出相位相反的两半波信号,去推动末级。也采用两个对称的、相同导电极性的管子推挽输出。⑤RC自倒相推挽式。利用一个推挽管集电极输出的倒相信号去激励另一个推挽管,进行推挽工作。详见本刊上期和本期的有关文章。
上述五种电路中,①②③三种是被广泛采用的,但①②两种优越性更大,用得更为普遍,本文将通过对典型电路的分析,介绍①②两种电路的工作原理和计算方法。
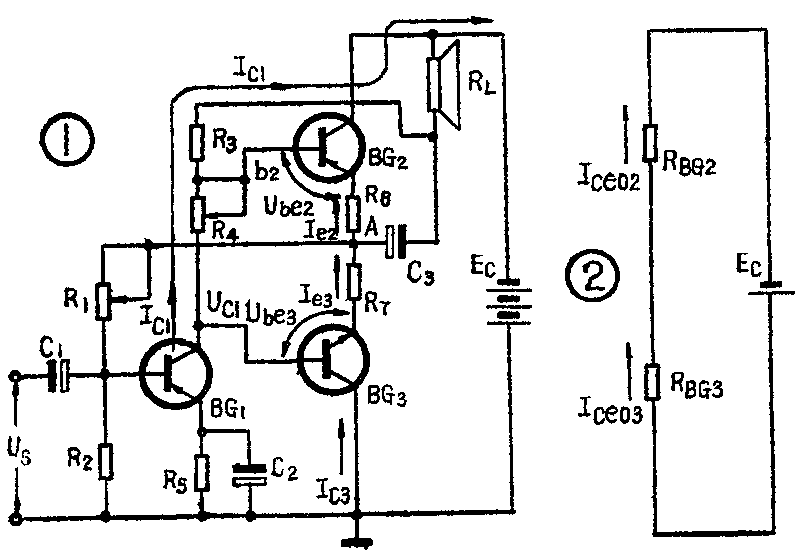
1.工作过程和原理:图1所示为辅助对称式OTL电路的典型电路。其中推挽管BG\(_{2}\)、BG3为导电极性不同,但性能、参数对称相等的中功率管或小功率管。它们可以用不同材料的管子,如PNP锗管(3AX、3AD型)和NPN硅管(3DG、3DK、3DA型)配用;但最好是用同一材料的管子,如将PNP硅管(3CG、3CK型)和NPN硅管配对使用,或将PNP锗管和NPN锗管(如3BX型)配用。后面将说明:只有用同一材料的管子组成推挽管,推挽两臂的对称性才能基本得到保证。推动管BG\(_{1}\)可用锗PNP型小功率管,但就温度稳定性来说,最好还是用硅PNP型小功率管。
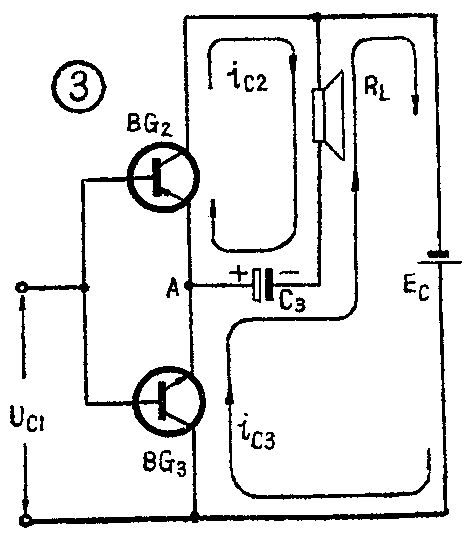
在静态(即无信号输入)时,耦合电容C\(_{1}\)、C3和旁路电容C\(_{2}\)都可看作开路。推挽管BG2、BG\(_{3}\)工作在乙类,两管处于截止状态。仅有穿透电流Iceo通过。由于选管时β\(_{2}\)=β3,故可认为此时I\(_{c3}\)≈Ie3=I\(_{ceo3}\)=Ic2≈I\(_{e2}\)=Iceo2。故可将两管的c-e极比作两个大电阻,如图2所示,且R\(_{BG2}\)=RBG3,发射极电阻R\(_{6}\)=R7,其值很小可忽略。分压的结果,中点A的静态电位U\(_{A}\)=\(\frac{1}{2}\)Ec。BG\(_{2}\)、BG3管的基极偏压靠BG\(_{1}\)管的集电极电流Ic1流经R\(_{4}\)、R3、R\(_{L}\)来建立,故R4、R\(_{3}\)、RL不但是BG\(_{1}\)管的集电极负载,也是BG2、BG\(_{3}\)管的偏置电路。对BG3来说,R\(_{5}\)和BG1的c-e极间电阻之和是其上偏置电阻;R\(_{4}\)、Reb2和R\(_{6}\)之和是其下偏置电阻。对BG2来说,R\(_{L}\)和R3之和是它的上偏置电阻;R\(_{4}\)、Reb3和R\(_{7}\)是它的下偏电阻。
为了使信号不失真地放大,并有足够的功率推动输出管BG\(_{2}\)、BG3,一般总是让推动管BG\(_{1}\)工作在甲类。Ic1可以调偏置电阻R\(_{1}\)来确定。R1不接到电池负端,而是接到中点A,是为了取得电压负反馈,以稳定放大器的工作点,尤其是稳定中点电位U\(_{A}\)。譬如,若环境温度升高,引起锗管BG2的I\(_{c2}\)增大,使A点对地负压减小。UA经R\(_{1}\)、R2分压后,在R\(_{2}\)上的负压,即BG1管基极的负偏压也相应减小,使I\(_{c1}\)减小,Ic1在R\(_{4}\)上的压降Ic1R\(_{4}\)也减小,BG2基极偏压往正向提高,从而又使I\(_{c2}\)减小,将UA拉了回来。这一反馈过程可表示为:
T\(^{0}\)↑→I\(_{c2}\)↑→UA↓→U\(_{b1}\)↓→Ic1↓
→I\(_{c1}\)R4↓→U\(_{b2}\)↓→Ic2↓→U\(_{A}\)↑
由于这一电压负反馈作用,使U\(_{A}\)始终稳定在Ec/2。这对放大器不失真功率的提高是很重要的。
I\(_{c1}\)的大小确定之后,推挽管的静态工作状态就要调R4来确定。譬如要让BG\(_{2}\)、BG3工作在甲乙类,即两管有一定的静态电流而且相等,即I\(_{e2}\)=Ie3,可以调R\(_{4}\),使Ic1R\(_{4}\)=Ube3+I\(_{e3}\)R7+U\(_{be2}\)+Ie2R\(_{6}\)。为调整方便,R4通常采用电位器,即用一个固定电阻与一个电位器串联或并联。
R\(_{4}\)的变动,可以改变推挽管的工作状态,但同时也会影响推动管的工作状态,因为R4也是推动管集电极负载的一部分。为了减少R\(_{4}\)对BG1管的影响,一般总是使R\(_{4}\)《R3,使R\(_{3}\)成为BG1管集电极负载的主要部分。
下面分析动态时的工作情况。
在动态时,图1中的电容C\(_{1}\)、C2都可看作交流短路。输入信号U\(_{S}\)就直接加到BG1管的发射结b-e间,放大后从集电极对地间输出的信号电压U\(_{c1}\)就成了BG2、BG\(_{3}\)的输入信号。如果忽略R6、R\(_{7}\)推挽级的工作情况就可以用图3等效简图来说明。
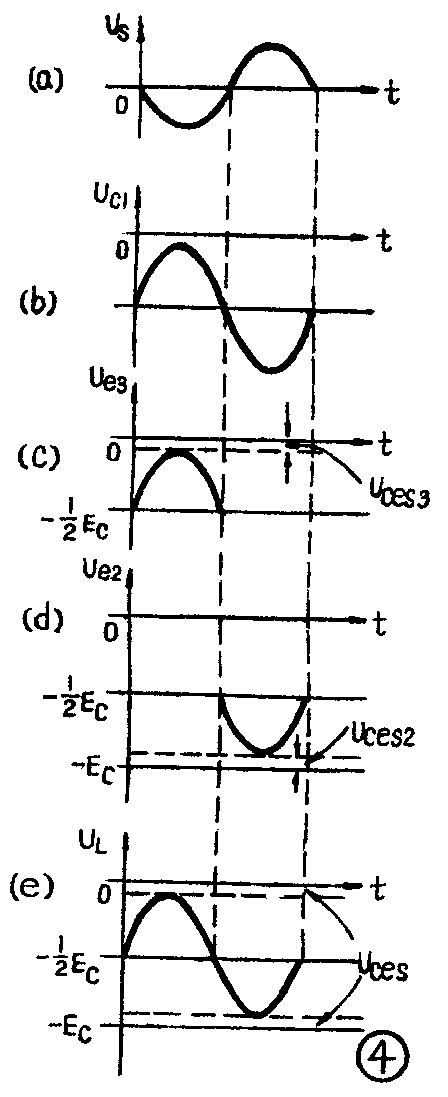
当输入信号为负半周时,其波形如图4(a),经BG\(_{1}\)管放大、倒相后输出的Uc1为正半周,如图4(b)。U\(_{c1}\)加到推挽级输入端,对BG2来说,正半周的U\(_{c1}\)使它的发射结b-e上加反向偏置,故处于充分截止状态。与此同时,BG3的发射结却得到正向偏置而导通,有电流i\(_{c3}\)(≈ie3)流经负载R\(_{L}\),并向电容C3充电。只要输入信号幅度足够大,使BG\(_{3}\)饱和导通,其管压降Uce3就仅为饱和压降U\(_{ces3}\),如图4(c)所示,Uce3=U\(_{ces3}\),而Uces3较小,故中点A的交流电位就接近电池正端电位(0电位)。此时截止的BG\(_{2}\)管承受了最大的反向电压Ec,相当于电池电压E\(_{c}\)通过导通管BG3全部加到了BG\(_{2}\)管的c-e间。
当输入信号为正半周时,BG\(_{1}\)输出电压Uc1为负半周,与上述情况相反,BG\(_{3}\)充分截止,BG2饱和导通,其管压降U\(_{ce2}\)=Uces2,这时中点A的交流电位偏到接近于电池负端电位(即-E\(_{c}\)),如图4(d)。截止了的BG3管又承受了最大反向电压E\(_{c}\)。有人可能会问:当BG3截止时,BG\(_{2}\)的供电通路被切断,它靠什么供电?靠的就是电容C3在前半周时已充好的电压,当BG\(_{3}\)导通时,有电流ic3向电容C\(_{3}\)充电,极性如图3所示。因此,当BG2导通时,充电电压U\(_{c3}\)就经BG2向负载R\(_{L}\)放电,形成ic2,电容C\(_{3}\)在这时就代替了电池供电。
由图3可见,i\(_{c3}\)和ic2以正反不同方向交替地流过R\(_{L}\),在RL上就产生了交流电压U\(_{L}\)。由图4(c)可知,当BG3导通时,U\(_{e3}\)在-Ec/2~-U\(_{ces3}\)间变化,其波形和输入信号波形一致;而当BG2导通时,U\(_{e2}\)在-Ec/2~-(E\(_{c}\)-Uces2)间变化,如图4(d)。将图4(c)和图4(d)组合在一起,就成了图4(e),就可看出推挽级输出电压U\(_{L}\)随输入电压Uc1在-U\(_{ces3}\)~-(Ec-U\(_{ces2}\))间变化,当Uces2=U\(_{ces3}\)=Uces时,输出电压U\(_{L}\)的最大振幅是Ec-2U\(_{ces}\)。
显然,要使输出波形对称,即i\(_{c2}\)=ic3(等值反向),必须保持电容C\(_{3}\)上的充电电压Uc3=E\(_{c}\)/2,使电容C3在放电过程中,U\(_{c3}\)也不致下降过多。要做到这一点,就必须使放电时间常数RLC\(_{3}\)大于输入信号最长周期的几倍才行。大致可按下式进行估算:
C\(_{3}\)≥10\(^{6}\)/2πflR\(_{L}\)
式中:f\(_{l}\)为最低下限音频,单位为赫;RL单位为欧;C\(_{3}\)单位为微法。其中RL是已知的,一般只有几欧,所以放大器频响要求越宽、下限频率f\(_{l}\)要求越低,C3就要求越大。例如f\(_{l}\)=20赫,而RL=8欧,则可算得C\(_{3}\)≥1000微法。
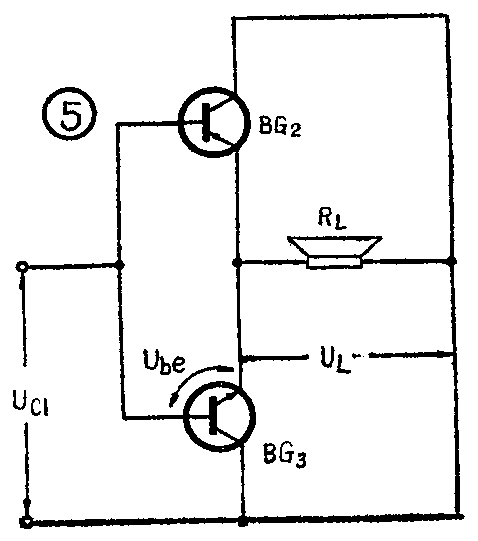
图3中,若将C\(_{3}\)看作对交流短路,电池Ec看作内阻为零的理想电源,则又可等效成图5电路。信号电压U\(_{c1}\)先后从两推挽管的b-c极间加入,负载电压UL则先后从两管的e-c间得到,集电极c就成了信号输入、输出的公共端点,因而可以认为互补电路实际上是两个推挽臂互相并联的共c电路,具有共c电路的一切特性,例如,从图5中可明显地看到,输出电压U\(_{L}\)和输入电压Uc1的关系为U\(_{c1}\)=Ube+U\(_{L}\),即UL<U\(_{c1}\),对两管来说都是这样。换句话说,这种互补电路的电压增益总是小于1的(即Kv≤1),但其电流增益还可以做到大于1,因而还可以有功率增益。此外,电路也有输入阻抗高、输出阻抗低的特性,因而它能省却输入、输出变压器。(待续)(金国钧)