想想看

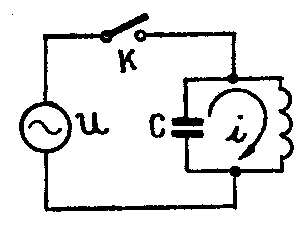
1．下图电路中，假若LC回路的谐振频率为f\(_{0}\)(30MHz），信号源u的信号频率为f1（35MHz），请你想一想，当开关K合上和合上后再断开时，LC回路中的电流频率是一样的吗？

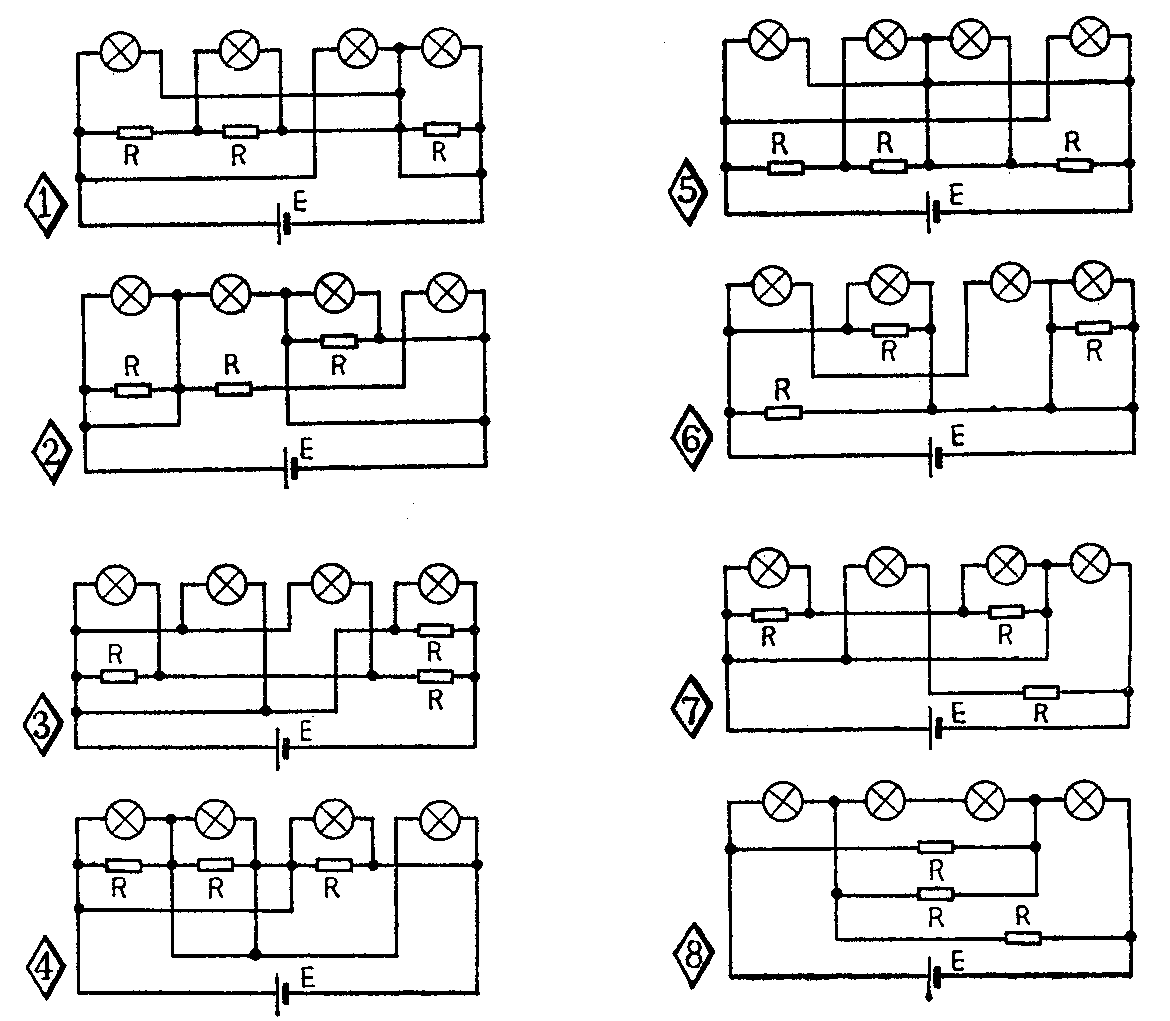
2．假定下图各电路中每只灯泡灯丝的电阻相同、各电阻的阻值相等、电池内阻可忽略不计，你能判断出各灯泡属于“亮”、“次亮”和“不亮”三种状态中的哪种状态吗？

1．小军说得不对。题中给出的1／8瓦、1瓦功率是电阻的额定功率，就是说当把这两个电阻接到电路里时，它们消耗的功率不能超过它们的额定功率，否则就要因过热而烧坏。但它们在电路中实际消耗的功率与流过电阻的电流及电阻阻值有关，即P\(_{耗}\)=I\(^{2}\)R。对于同一电路，假若需要1／8瓦1千欧电阻，那么，也就是说实际使用中，P耗＜1／8瓦。当用1瓦的1千欧电阻代替时，因流过电阻的电流、阻值都未变，所以它上面消耗的功率仍小于1/8瓦，并不因为所用电阻的瓦数大而费电。（胡西方）

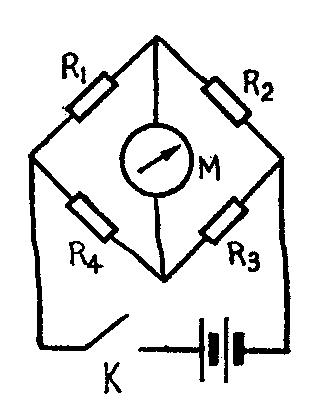
2．我们把灵敏检流计M与四只十进位的电阻箱R\(_{1}\)、R2、R\(_{3}\)、R4组成图示的直流电桥电路，加上直流电源E，就成为简单的“计算机”了。计算原理主要是根据电桥平衡条件R\(_{2}\)、R4=R\(_{1}\)、R3。作乘法运算时，将R\(_{2}\)调至被乘数的值，将R4调至乘数的值，再根据需要送取R\(_{3}\)=1、10、100、……10\(^{n}\)（n=1，2，3……），然后调整R1使电桥平衡即检流计指示为0。这时，若R\(_{3}\)=1，则R1上的读数便是我们要求的乘积，因为R\(_{1}\)·R3=R\(_{2}\)·R4，R\(_{1}\)=R2·R\(_{4}\)R3=R\(_{2}\)·R4;1=R\(_{2}\)·R4。若R\(_{3}\)=10n，则R1上的读数应再乘上10\(^{n}\)才是所求的乘积。

作除法运算时，从电桥平衡条件得到\(\frac{R}{_{1}}\)R2=R\(_{4}\);R3，把R\(_{1}\)调至被除数值，把R2调至除数值，根据需要选取R\(_{3}\)=1、1、10、100……10\(^{n}\)（n＝1、2、3……），然后调整R4使检流计指示为0，说明电桥平衡。若此时，R\(_{3}\)＝1，则R1R\(_{2}\)=R4;1=R\(_{4}\)，R4上的读数便是所求之商。若R\(_{3}\)=10n，则R4上的读数应除以10\(^{n}\)才是所求之商。（张富成）