谐振

我们都知道，在收音机电路中有好几个由电感线圈和电容器组成的振荡回路。这些振荡回路有一个奇妙的特性——谐振。收音机的输入电路就是依靠振荡回路的谐振特性，从许多不同频率的无线电波中，选出我们所需要的那一个。谐振电路在电子技术中应用极广，下面，介绍一些有关谐振的知识。

如果把一个小孩抱到秋千上，并用力推一下秋千座板，小孩就随着秋千来回摆动起来。这是什么原因呢？这可运用能量守恒与转化定律来分析。大人推一下秋千座板，使秋千离开平衡位置，外力对秋千以及小孩做了功，使它们获得重力势能。秋千在来回摆动过程中，能量是以动能和势能两种形式互相转换，使在座板上的小孩随着秋千来回摆动。如图1所示，当小孩摆到两端（A或B点）时，离地面位置最高，势能最大，摆动速度为零，动能最小。而当摆到中间位置（O点）时，离地面位置最近，势能最小，摆动速度最大，功能最大。由O点往前或后摆时，是动能向势能转换，而由A、B向中间摆时，是势能向动能转换。这种来回摆动，就叫做自由振荡。

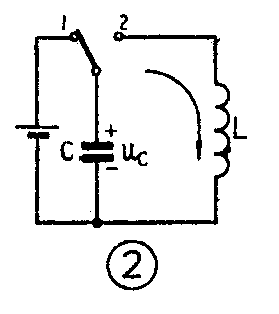
一个由电感电容组成的电路，如图2所示，如果先将开关倒向位置1，电池给电容器C充电，授给电容器以电能。然后将开关倒向位置2，电容就会对电感放电，在回路中产生电流（见图3），原来储藏在电容器中电场的能量开始变成电感线圈中磁场的能量，当电容器放电完毕，电能全部转化为磁能，这时电流i最大；接着回路电流开始减小，电感中产生的感生电动势对电容C充电，但现在电容上电压方向与原来相反，当能量又全部回到电容器中后，又开始对线圈L放电，可是现在电流的方向又与以前相反了，这样在回路中发生了电容器中的电能和电感线圈中的磁场能相互不断转换的物理过程。

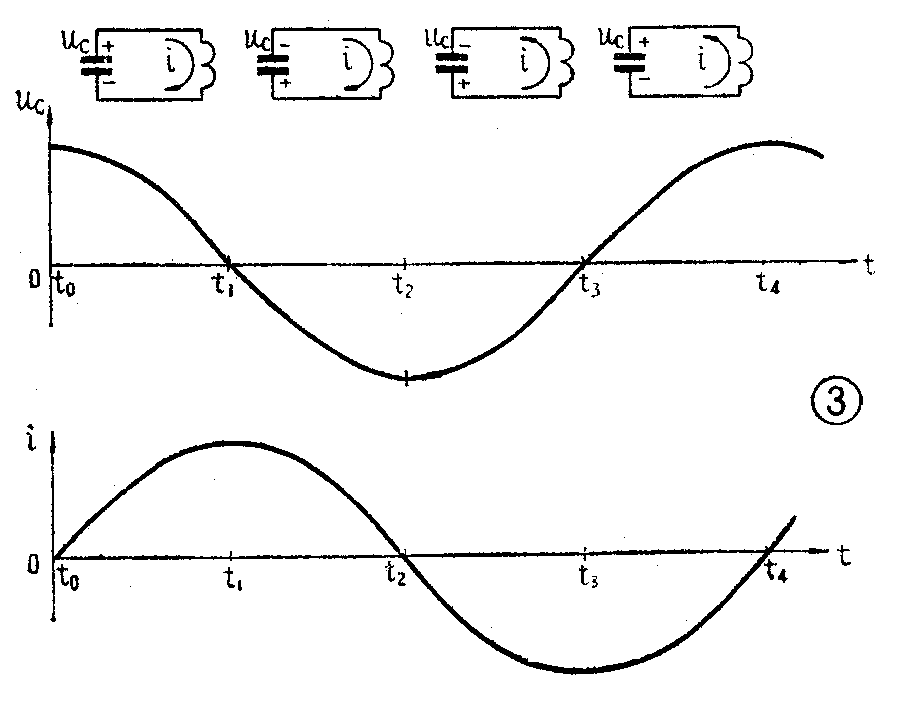
在图3中画出了电容器上电压和回路中电流的波形，以及标出了每一段时间电容器上电压极性和回路中电流的流动方向。如果我们忽略了振荡回路中的所有损耗，振荡就能一直持续下去，这是理想的振荡过程。

这种外界能量一次授予后，任其自由互换而产生的振荡，称为自由振荡。自由振荡的频率——每秒振荡的周期数，称为固有振荡频率。

在上述LC振荡回路中，由于存在着阻尼电阻（如电感L中的损耗电阻），每振荡一次都要损耗一定能量，因而振荡将不断减弱，这叫阻尼振荡。如果电感线圈和电容器组成的振荡回路和一个交流电源连接（如图4所示），电源不断向回路提供能量，回路中就会产生和外加电源频率相同的振荡电流，这就叫强迫振荡。强迫振荡与自由振荡的区别在于强迫振荡的频率决定于电源频率而自由振荡的频率决定于回路的参数。

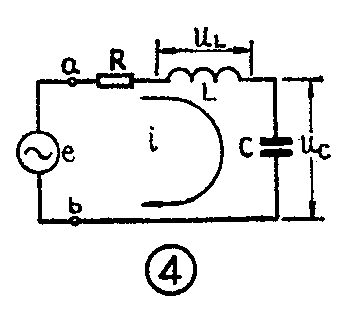
在振荡回路中有所谓谐振现象。如果外加交流电源的频率和回路的固有频率相同时，回路中产生的电流最大，能最大限度地从电源吸取能量，而不会有能量返回电源，这就叫做谐振。

振荡回路的谐振，按信号源（能源）和电路元件的连接方式不同，可分为串联谐振和并联谐振。下面我们分别来谈谈这两种情况。

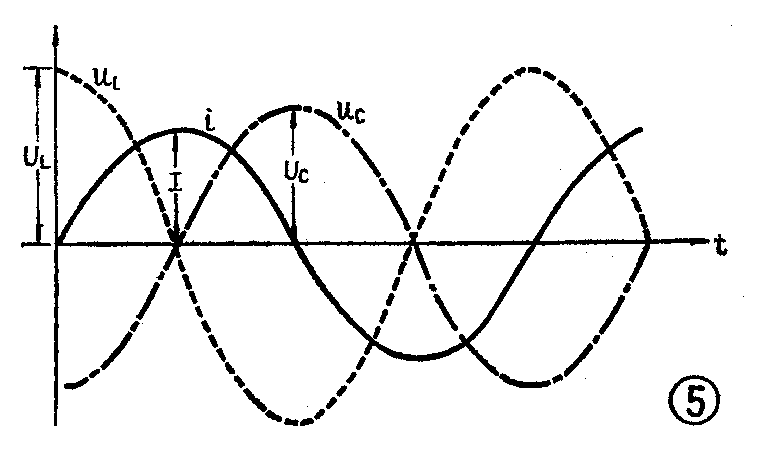
在图4中，电感L、电容C和电源e相串联。在这种串联电路中产生的谐振，就叫做串联谐振。它的电流、电压波形如图5所示。用实线画出电流i的波形，因为串联电路中电流处处相同，所以流过电感L、电容C和电阻R的电流是同一个电流。但是，三个元件L、C和R两端的电压可并不一致，电感两端的电压u\(_{L}\)超前于i90°，如图5中虚线所示。而电容两端的电压uc则落后于电流i90°，如图5中点划线所示，电阻R二端的电压u\(_{R}\)与i同相。这样，uL和u\(_{C}\)的相位正好相反，uL为正时，u\(_{C}\)正好为负。因此两个电压串在一起是互相对消的。我们知道，电感L两端的电压UL=X\(_{L}\)I，其中XL=2=πfL，是电感线圈的电抗，是流过电感L的电流。电容C两端的电压U\(_{c}\)=XcI，其中X\(_{c}\)=\(\frac{1}{2πfc}\)，是电容器的电抗。从上面XL和X\(_{c}\)的表示式可看出，感抗XL随频率的升高而升高，而容抗X\(_{c}\)随频率的升高而减小。在某一频率fo，满足2πf\(_{o}\)L=1;2πfoc时，感抗和容抗相等，电感两端的电压和电容两端的电压相等，相互对消，电路中从电源的连接点向回路看进去的阻抗等于电阻R，此时回路的总阻抗最Z=R，电流I最大I=\(\frac{U}{R}\)。这种情况叫做串联谐振。可见，谐振的条件是X\(_{L}\)=Xc，即2πf\(_{o}\)L=1;2πfoc,由这个式子可求得谐振频率f\(_{o}\)=\(\frac{1}{2π}\)\(\sqrt{LC}\)这个频率也就是回路的固有振荡频率。

当外加电源频率f小于f\(_{o}\)时，则Xc大于X\(_{L}\)，回路呈现容性，其值为（Xc－X\(_{L}\)），回路的总阻抗为Z=\(\sqrt{R}\)\(^{2}\)+（Xc-X\(_{L}\))2，比R大，故电流减小。f比fo低得越多，总阻抗Z也就越大，电流I也就越小。与此类似，外加电源频率f高于f\(_{o}\)时，XL比X\(_{c}\)大，此时回路呈现感性，其值为XL－X\(_{c}\)，回路总阻抗也比R大，电流也会减小，f高得越多，电流也就越小。在图6中，画出电流随频率而变化的曲线，这条曲线称为串联回路的谐振曲线。

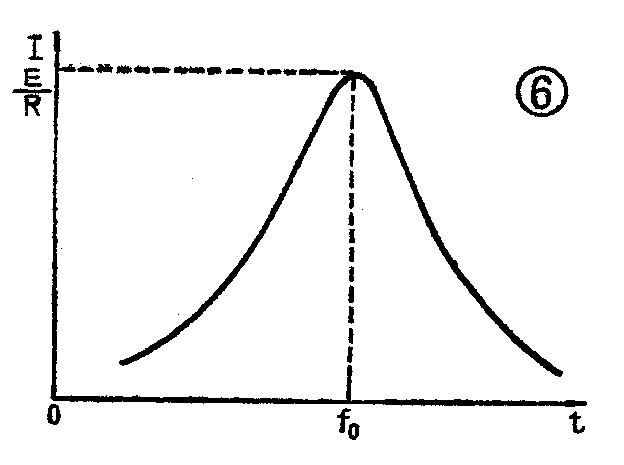
为了说明谐振特性，常把回路在谐振时的感抗或容抗与电阻的比，叫做LC回路的品质因数，用符号Q表示，称为Q值。Q=ω\(_{0}\)LR=1;ω0RC,这是一个重要的参数。Q值的物理意义是指回路中谐振时每周期内贮存能量和消耗能量之比的2π倍。谐振时，电源供给的能量恰好是补偿回路由于阻尼而耗失的能量，故回路中贮存能量不变。这样，我们可以很方便地用电感中贮存的能量最大值（此时电容中贮能为零）或是电容中贮存能量最大值（此时电感中贮能为零）来代替整个回路贮能总值。电感线圈贮能最大值为12LI\(^{2}\)，回路一周期消耗能量等于功率1;2I2R乘周期T，于是Q=2π×1;2LI\(^{2}\);\(\frac{1}{2}\)I2R×T=2πL;RT，因为频率f\(_{o}\)是周期的倒数，上式可写成

又因为谐振时X\(_{L}\)=Xc，所以Q也可以写成\(\frac{X}{_{c}}\)R=1;2πfocR。Q值愈高，代表回路中贮存能量相对于消耗能量之比愈大。Q值用回路参数表示，可得Q=\(\frac{1}{R}\)\(\sqrt{L;C}\)从式中可以看出R越大，Q值越小，则谐振曲线较平坦；R比较小，Q值就较大，则谐振曲线较尖锐，如图7所示。

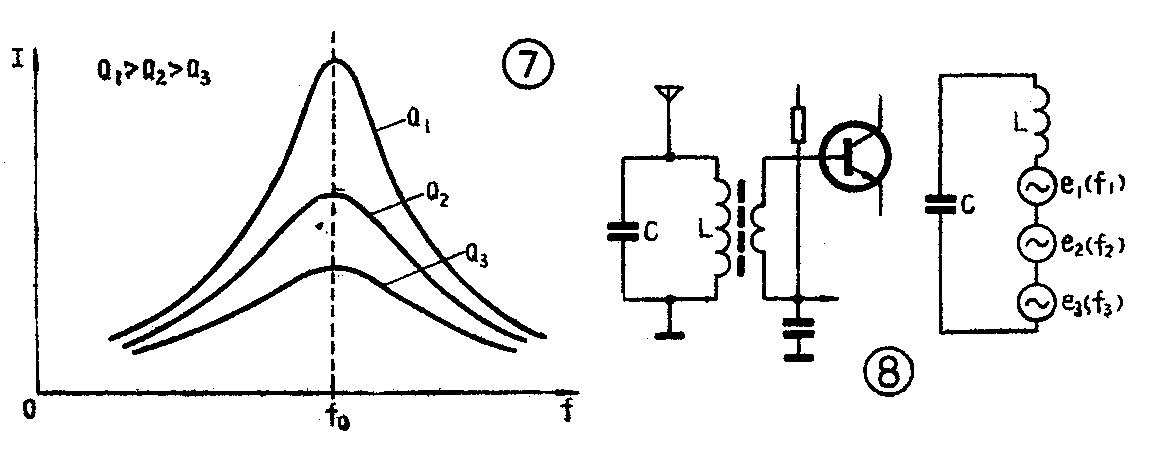
当发生谐振时，电路中电抗元件上的电压IX\(_{L}\)（或IXc）与电阻上的电压IR（它等于电源电压）之比等于Q，这就好象把电源电压放大了Q倍。应注意的是电压放大并不意味着能量放大，因为电抗中的能量是外电源作用下逐步贮存起来的。

图8左边是大家所熟悉的收音机的输入回路。每个广播电台发出的无线电波都在天线回路中产生一个高频交变电动势。在图8右边，示出三个不同频率的电台分别在输入回路中产生频率为f\(_{1}\)、f2、f\(_{3}\)的高频电动势e1、e\(_{2}\)和e3。比如说，我们需要收听电台1，可以改变电容c或电感L,使得f\(_{0}\)=\(\frac{1}{2π}\)\(\sqrt{LC}\)=f1,则根据串联谐振的原理，回路对频率f\(_{1}\)的阻抗为最小，这时回路中产生频率为f1的电流将是最大。这个电流流过电感线圈，就会在变压器的次级线圈中感应产生一个很大的电压，加到收音机输入级晶体管的基极上。与此同时对于其它频率的阻抗要比对f\(_{1}\)的阻抗大得多则e2和e\(_{3}\)在回路中产生的电流很小，变压器次级线圈产生的频率为f2和f\(_{3}\)的高频电压也就很小。这样，利用串联谐振的这种特性，回路就把电台1发出的无线电波挑选出来，收音机的扬声器里就能发出电台1的播音。

前面介绍串联谐振的电路时，我们没有特别提出信号源内阻的问题，实际上我们是认为信号源内阻近似等于零为条件的。要是考虑信号源内阻，它是和R串联的。设信号源内阻为R\(_{S}\)，这样，回路的品质因数就应是\(\frac{ωL}{R}\)S+R。如果R\(_{S}\)相当大，Q值就会相当小。Q小了谐振现象就不显著。为了解决这个问题，可以改用并联谐振回路，就是把电感、电容并联连接，再和信号源并联起来，如图9（a）所示。这里为了分析问题的方便，我们将信号源用一个恒流源is和内阻R\(_{S}\)相并联表示。所谓恒流源，就是指无论负载多大，它给出的电流是一个恒定值。此外，为了简化问题，我们先研究回路没有损耗的理想情况。

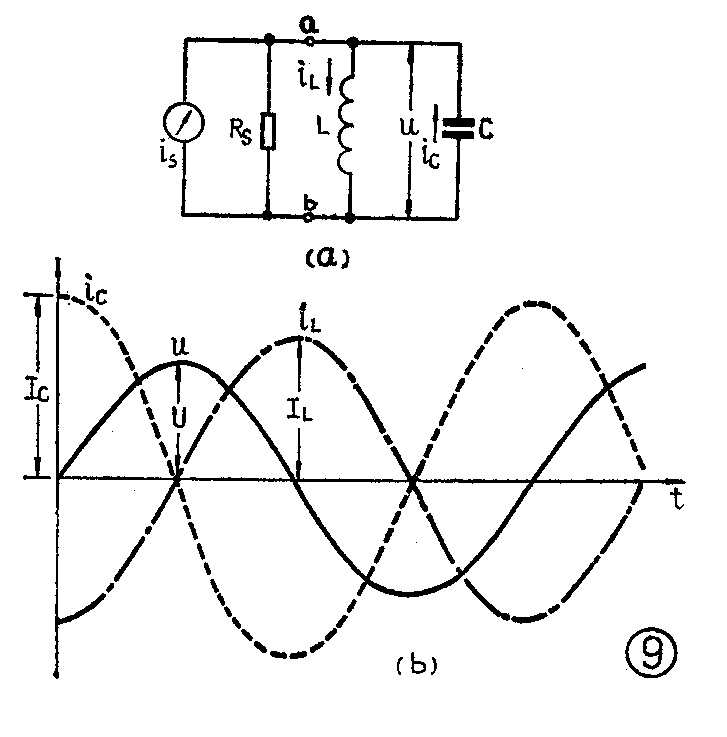
在图9（b）中，我们画出并联电路中的电流、电压的波形。这里电感L和电容C两端的电压是相同的，u\(_{L}\)=uC＝u。图中用实线表示电压u的波形。流过电感的电流i\(_{L}\)在相位上落后于电压u90°，流过电容C的电流iC则超前于u90°。从图中我们看到，在任何时刻,i\(_{L}\)和iC的方向总是相反的。如果电流i\(_{L}\)是正的，由a端流向b端，那么iC就是负的，由b端流向a端。由于i\(_{L}\)和iC的方向恰好相反，因此，从外接电源向回路看去，它们有相互抵消的趋势。

当外加电源的频率等于回路的固有振荡频率f\(_{0}\)=\(\frac{1}{2π}\)\(\sqrt{LC}\)〗时，就发生谐振。在f=f0时，X\(_{L}\)＝XC，因此I\(_{L}\)=U;XL和I\(_{C}\)=\(\frac{U}{X}\)C相等，也就是说i\(_{L}\)和IC大小相等，方向相反，它们完全抵消。实质上是电感、电容之间交换能量，信号源不向X\(_{L}\)和XC提供能量，故从信号源向这两个电抗看去的阻抗为无限大。

对其他的频率，由于X\(_{L}\)和XC不相等，i\(_{L}\)和iC不能完全抵消，这时信号源电流就有一部分要流入电感、电容，回路和信号源之间将发生能量交换。自然，回路的总阻抗将比谐振时小，频率偏离f\(_{o}\)愈多，阻抗减小也愈多。同样可画出类似于图6的谐振曲线，只不过应将纵坐标换成回路两端的总阻抗，即阻抗Z与频率f的关系曲线称为并联电路的谐振曲线。

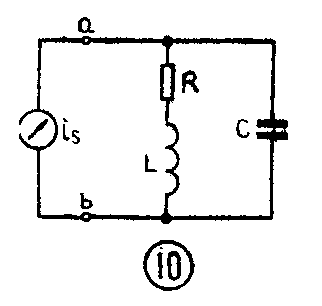
然后我们研究回路中有损耗的情况，考虑线圈的铜损电阻R，可得到图10所示电路。为了简化，我们认为信号源内阻为无限大，把R\(_{S}\)视为开路。谐振时，仍然是电感和电容交换能量，信号源只提供电阻R所消耗的能量。由于电感支路中有电阻R,故谐振频率将稍有变化，当回路的Q值很高时，可以近似地认为谐振频率仍为fo。谐振时回路两端电阻达到最大值，但由于有了电阻R不是无限大了。经过计算，Z\(_{max}\)其值为LCR。称作“谐振阻抗”。

对并联谐振回路，Q值的定义仍然和串联谐振回路一样，其值也是Q=\(\frac{X}{_{L}}\)R=XC;R。

当电路发生并联谐振时回路两端的电压

可见，并联谐振时，回路中的电流是信号源电流I\(_{S}\)的Q倍。所以，并联振荡回路在谐振时，好象把信号源电流放大了Q倍。故有时称并联谐振为电流谐振，而称串联谐振为电压谐振。

顺便指出，在并联谐振回路中，恒流信号源的内阻R\(_{S}\)是与电抗元件并联的。当电阻RS越大时，则流过R\(_{S}\)的电流越小，而进入回路的电流则相对地越大，即消耗的能量相对地越小，而贮存于回路中的能量相对地较大，Q值也就越高，正好与串联谐振回路相反。

从前面的讨论我们看到，一个振荡回路的Q值超高，则当谐振时，回路电抗元件中的电流或其两端的电压比不谐振时增大得越多，即谐振特性越显著，选择信号的本领越强。所以我们要致力于提高回路Q值。

任何一个实际应用的振荡回路，都不免要和负载和信号源相连接。在前面讨论问题过程中，我们知道当电阻与振荡回路的电抗元件串联时，流过它们的电流相同，电阻越小，消耗能量相对地越小，Q值就越高。当电阻和振荡回路的电抗元件并联时，加到它们上面的电压相同，电阻越大，消耗能量相对地越小，Q值就越高。所以当负载电阻较小时，为了获得较高的Q值，应将负载电阻和回路电抗元件串联；而当负载电阻较大时，应将负载电阻和回路电抗元件并联。根据同样的道理，当信号源内阻较小时，宜采用串联振荡回路，而当信号源内阻较大时。宜采用并联振荡回路。

晶体管是一个内阻大的电子器件，所以收音机中的高频放大器和中频放大器，都采用并联振荡回路作为负载，使回路能有高的Q值，以便使电路有较好的选择性。

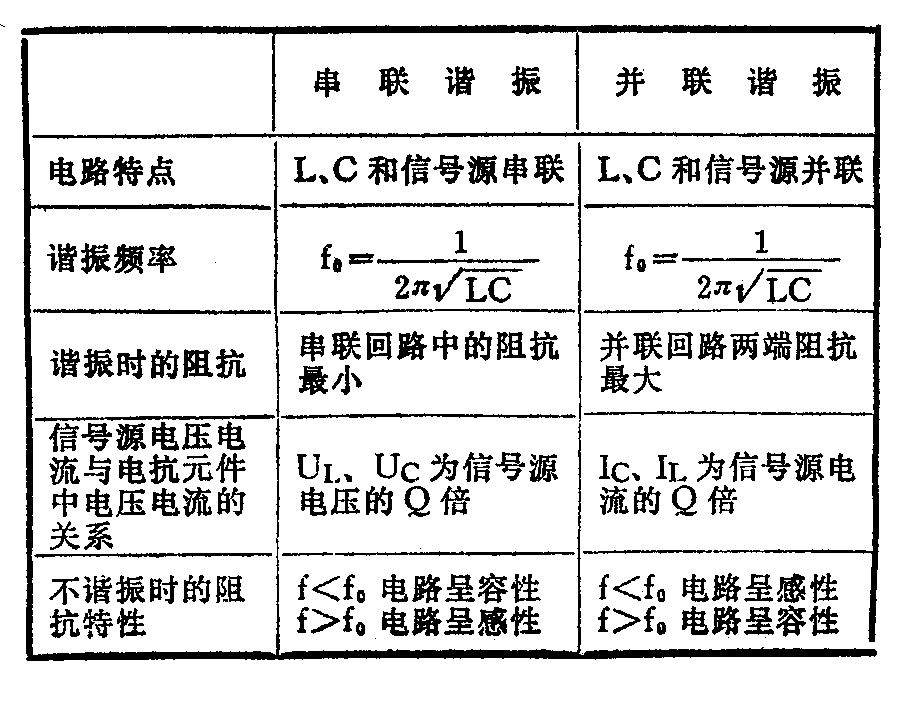
最后，我们将串联谐振和并联谐振的特点列表进行比较。（魏群）