在电工和无线电技术中,经常要碰到按正弦规律变化的周期过程。例如发电机发出的交流电,在电感电容回路中产生的正弦振荡,等等。
一个质点M沿圆周作等速运动,如图1所示,就是一种最简单的周期运动。如果以A点为起始点,那么,M点在任一时刻的位置,都可以用从OA起转过的角度φ\(_{m}\),来表示。这个角度φm就叫做该周期过程的相位,它完全确定了M点在这一瞬间的位置,也就是周期过程所处的状态。
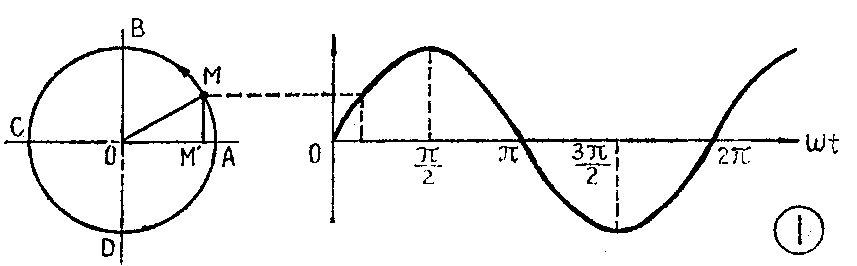
大家知道,当M点作等速圆周运动时,它的纵坐标MM′就是按正弦规律变化的。设t=0时,M是在A点,则MM′随时间变化的曲线如图1所示。从图中可以很清楚的看到
MM′=Asinφ\(_{m}\)=Asinωt
式中A是正弦振荡的幅度,φ\(_{m}\)就是相位,ω是M点绕O点转动的角速度。M每转一圈,就转过了2π弧度。因此,如果M转动的频率即每秒钟转动的圈数为f,那么,角速度ω=2πf。
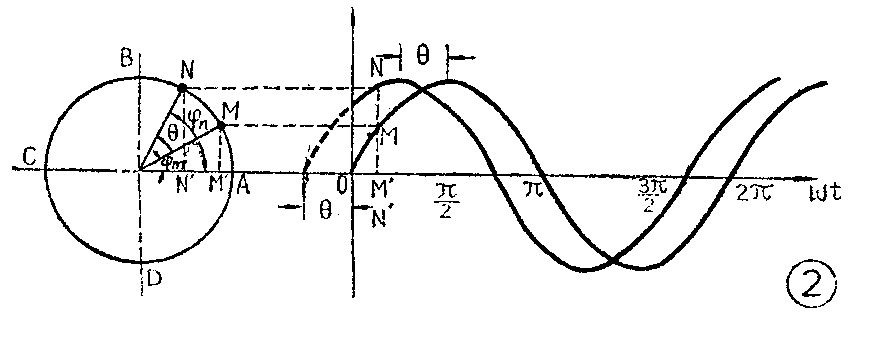
现在设在M点前面有一个质点N也以相同的速度沿圆周运动,如图2左边所示。那么,NO和MO的夹角θ在转动过程中总是保持不变。如果M点在某一瞬间的相位是φ\(_{m}\)=ωt,那么,N点的相让φn=ωt+θ,这时N点的纵坐标
NN′=Asinφ\(_{n}\)=Asin(ωt+θ)
图2右边分别画出了 MM′和NN′随时间变化的曲线。
由图2可见,当t=0时,M点是在A点,它的相位为0;而质点N的相位不等于0,而是等于θ。t=0时的相位,即起始相位,叫做初相。M点的初相为0,N点的初相为θ。N点和M点的相位差为φ\(_{n}\)-φm=θ,它等于两过程的初相之间的差别。从图2可以很清楚地看到,N点的运动过程比M点领先一个角度θ,例如,N通过B点(最大值)之后,要经过一段时间(\(\frac{θ}{ω}\)),M才会通过B点。我们说,N点比M点超前一个角度θ,或者说,M点比N点落后一个θ。
如果θ=0,即M和N点重合,我们就说这两个过程相位相同,或者叫做同相;如果θ=π=180°,就说这两个过程相位相反,或者叫做反相。
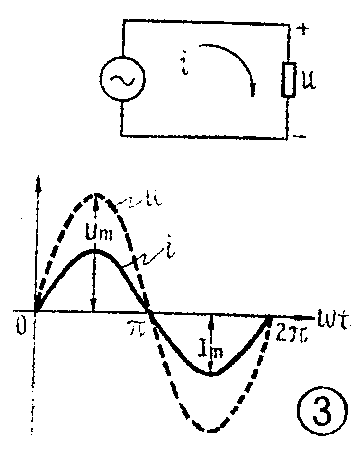
如果把一个交流电压u=U\(_{m}\)sinωt加到电阻R两端,如图3所示(图中箭头和正、负号分别代表电流和电压正方向)。根据欧姆定律,i=\(\frac{u}{R}\)=Um;Rsinωt=I\(_{m}\)sinωt(这里Im=\(\frac{U}{_{m}}\)R)。电压和电流的变化曲线如图3中所示,i和u同时为0,又同时增大达到最大值,再同时减小到0。这就是说,电流i和电压u是同相的。
如果把一个交流信号u\(_{sr}\)加到晶体管放大器的输入端(见图4),那么,当usr增大时,集电极电流i\(_{c}\)增大,Rc上的电压降增大,而集电极电压减小,所以输出电压u\(_{sc}\)减小,其变化曲线如图中所示。由图可见,输入电压usr和集电极电流i\(_{c}\)同相,和输出电压usc反相。
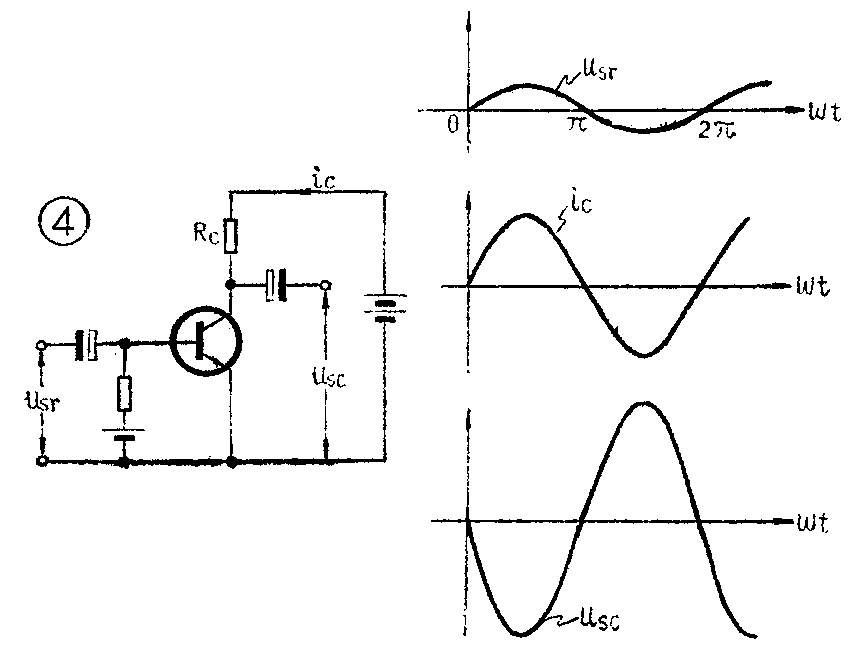
现在分析一下交流电通过电感L和电容C的情况。
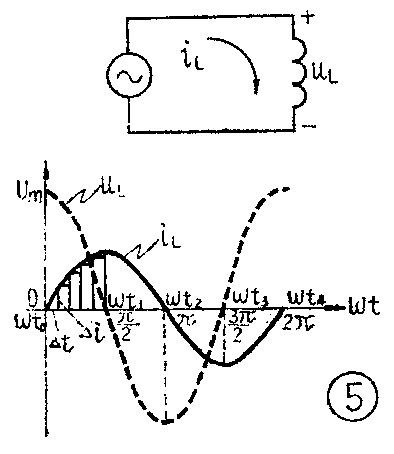
我们知道,当线圈中的电流变化时,在线圈两端会产生自感电动势e\(_{L}\),它的大小eL=|L\(\frac{Δi}{_{L}}\)Δt|。在纯电感电路中,这个自感电动势也就是电感两端间的电压uL,所以u\(_{L}\)=|LΔiL;Δt|。在图5中,从t\(_{0}\)到t1期间,i\(_{L}\)是增加的,这时自感电动势反抗电流的增长,上正下负,即电压uL是正的。但电流增加的速度(\(\frac{Δi}{_{L}}\)Δt)越来越小,所以uL以最大值U\(_{m}\)逐渐下降。到t1瞬间电流不再增加,所以u\(_{L}\)为0。过了t1以后,电流i\(_{L}\)开始减小,自感电动势阻止电流的减小,下正上负,uL变成为负的。在t\(_{1}\)到t2期间,电流减小的速度越来越大,所以u\(_{L}\)的负值越来越大。到t2时增长到最大值-U\(_{m}\)。以后,iL反向增加,所以u\(_{L}\)仍为负的,不过iL的增加速度逐渐减小,所以u\(_{L}\)的绝对值也越来越小,到t3时减小到0。在t\(_{3}\)到t4期间,反向电流逐渐减小,u\(_{L}\)又变成正的,而且越来越大。从图5画出的曲线可以看出,iL比u\(_{L}\)落后90°(π;2)。
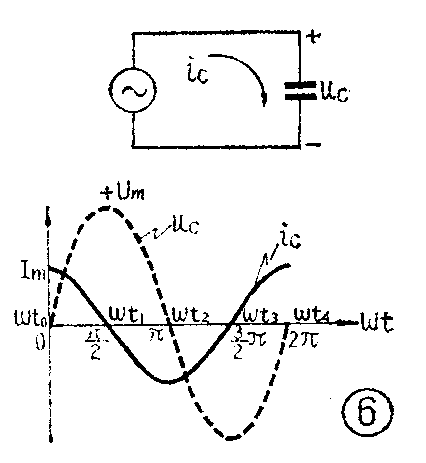
下面再来看电容上的电压与电流的相位关系。我们知道,电容器上的电荷Q与其两端的电压u\(_{c}\)成正比,即Q=Cuc,而电流是电荷的变化率,所以i\(_{c}\)=\(\frac{ΔQ}{Δt}\)=CΔuc;Δt。和前面分析电感的情况相似,设在t=0时,正弦电压u\(_{c}\)从0开始增长,这时ΔucΔt最大,故充电电流i\(_{c}\)为正的最大值Im。从t\(_{0}\)到t1期间,电压增加速度逐渐减小,i\(_{c}\)也就随着减小,到t1时,u\(_{c}\)达到最大值,此时Δuc;Δt=0,所以i\(_{c}\)=0。从t1到t\(_{2}\)期间,uc逐渐减小,\(\frac{Δu}{_{c}}\)Δt变为负值,电流改变了方向,这相当于电容器放电的情况。由于uc减小的速度越来越快,放电电流i\(_{c}\)就越来越大,当t=t2时,i\(_{c}\)=-Im。以后,u\(_{c}\)反向增加,所以ic仍为负值,这相当于电容器反向充电的情况。不过由于u\(_{c}\)增加的速度越来越小,所以ic的绝对值越来越小,到t\(_{3}\)时减小到0。在t3到t\(_{4}\)期间,反向电压逐渐减小,ic又变成正的,而且越来越大,到t\(_{4}\)瞬间达到最大值Im,从图6中可以看出,i\(_{c}\)的相位比uc超前90°(π;2)。(张茂昌)