地下线的测试方法

地下线的测试是建设和维护地下线的一项很重要的工作。地下线工程施工前对线材的测试，施工过程中和施工完毕后对地下线的测试检查，日常维护和查找故障的测试，是保持地下线质量，保证地下线正常工作的重要一环。所以，在建设地下线的过程中，必须运用和掌握正确的测试方法，认真做好测试工作，建立好技术档案（测试卡），并对所测数据进行分析研究，从而探索并掌握地下线的变化规律。

1．用千分卡或游标尺分别抽测地下线芯线、绝缘层、护套层的直径和厚度，并进行记录，同时记下地下线所使用的材料，供以后校核时参考。

2．导线通断测试。可用万用表欧姆档测试芯线的直流电阻，其阻值应接近表1所列数值。如果直流电阻过大，则表示导线接头接触不良。应找出原因并进行处理后才可使用。

3．绝缘电阻（漏电）的测量。将导线置于0.3％的盐水中，浸泡24小时以后用2500伏摇表（兆欧表）测试，应不发生击穿现象。然后用1000伏摇表测试，在水温为20℃时，以聚氯乙烯为绝缘外皮的导线，其绝缘电阻不应小于20兆欧／公里；用聚乙烯绝缘的导线，其绝缘电阻不应小于100兆欧／公里。测量时，摇表的接地端通过一根导线与水接通，另一有保护环的端子接导线芯线一端，芯线的另一端应与水绝缘。测量完后应对芯线进行放电。

双芯线除测量每一芯线对水的绝缘电阻外，还要测量双线间的绝缘电阻，一般说来其阻值应为单芯线的两倍。

如果导线的长度不是一公里，可按下式换算出每公里的绝缘电阻的兆欧数：

上式中L代表地下线的实际公里数；R为实测的绝缘电阻（兆欧）。

1．环路电阻的测量：①对于双线回路，可在终端将两芯线短路，用直流电桥（例如850型）在始端测量直流电阻，其阻值（双环）应接近计算值。计算公式为R=R\(_{0}\)·L（欧），式中R0为该种地下线每公里的环路电阻，单位为欧／公里，L为地下线的长度，单位为公里。②对于单线回路，测量时应在线路两端装设接地良好的地线，以代替另一导线，使其构成回路。测试方法与双线回路相同。测试数值应接近于单线每公里的直流电阻值与线路长度的乘积，线路每公里的直流电阻值可查表1。

2．绝缘电阻的测量：测量方法与埋设前的测法相同。由于接头漏电等因素的影响，每公里的绝缘电阻较埋设前会有所降低。以聚氯乙烯为绝缘材料的地下线，其对地绝缘电阻不应小于10兆欧／公里；以聚乙烯为绝缘材料的地下线，对地绝缘电阻不应小于50兆欧／公里。双线间的绝缘电阻应为单线对地绝缘电阻的两倍。

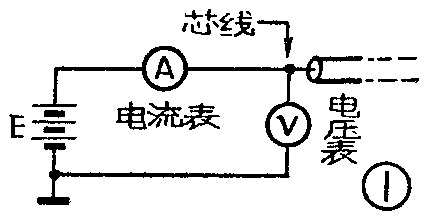
在绝缘电阻小于1兆欧时，用摇表测量不容易读出读数，这时可采用万用表测量。用万用表测量应测二次，第二次的表笔要与第一次接法相反，然后取两次测量的平均值。有的地区干扰信号太大，用万用表也测不准确，这时可用电压、电流法测量，仪表的连接方法如图1。电源采用叠层电池，每块22.5伏，多块串联而成。串联后的电压应在150伏～220伏范围内。电流表和电压表可用同一块三用表代替，先测出漏电电流I，再测出芯线对地的电压U，则绝缘电阻为R=UI（欧）。

3.回路电容的测量：可使用WQJ—05、WQ—5或其它型号的万能电桥测量。测量双线回路时，在终端将两芯线悬空（开路），始端将两芯线接仪器的两测量端子。仪器的测量选择开关置于“C”档，倍率开关放在适当位置。反复调整数字旋钮和损耗因素旋钮，使电桥达到平衡，这时数字旋钮所指就是线路电容量。测量单线对地电容时，始端应装设一个良好的地线以构成回路。

4.回路电感量的测量：测量回路的电感也采用万能电桥。测量双线电感时，应在终端将两芯线短路，始端将两芯线接至仪器两测量端子，测量选择开关置于“L”档，倍率开关扳至相应的适当位置。反复调整数字旋钮与品质因数（Q值）旋钮，使电桥平衡，数字旋钮所指示的即为电感量。测量单线回路电感时，终端和始端均应装设良好的地线。

测量出回路的电容或电感后，除以回路的长度（公里），所得的商即为该地下线每公里的电容值或电感值。在测量中，如果回路太长，电桥不易平衡，可在1公里的测试杆处拆断线路进行测量，测量结果即为该地下线的每公里电容或电感。

5．阻抗的测量：测量回路的阻抗时，应使用专门测量阻抗的阻抗电桥，它能测出阻抗的电阻部分（R）和电抗部分（±jX），并且能测出电抗是感抗还是容抗。

在有线广播中常用比较法测量阻抗，它能测出阻抗的模数（绝对值），即

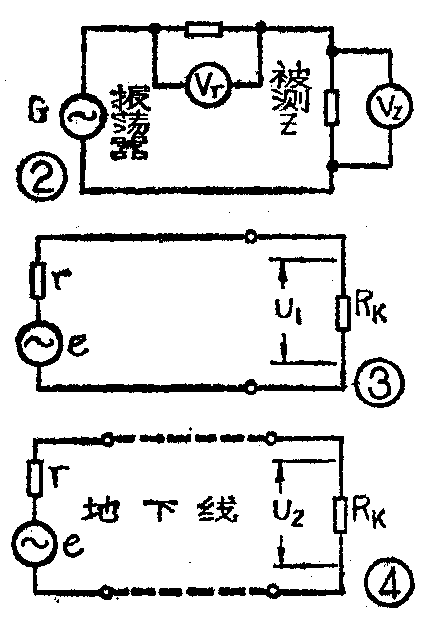
用比较法测量阻抗的线路如图2。图中G为振荡器，R为标准电阻，V\(_{r}\)、Vz为真空管或晶体管电压表，Z为被测阻抗。电路接通以后，有电流流通，在R上的电压降U\(_{r}\)可以从电压表Vr上读出，在Z上的电压降U\(_{z}\)可从Vz上读出。此时被测阻抗的模数为

如果将图2中的标准电阻R换成标准电阻箱，也可以采用如下的简便方法来测量阻抗。即在线路接通后，反复调节R，使V\(_{r}\)与Vz读数完全相等，这时电阻箱R的数值就是被测阻抗Z的模数。为了测量准确，测量U\(_{r}\)和Uz时应使用同一毫伏表和同量程档。测试地下线的输入阻抗和特性阻抗，可按如下方法进行。

①地下线输入阻抗Z\(_{in}\)的测量：线路终端接上负载电阻Rk，在始端按上述方法测量其阻抗，此阻抗值即是线路终端接R\(_{k}\)时在某一频率下的输入阻抗。在较近距离和频率较低时，其输入阻抗随着Rk的改变而变化。

②地下线特性阻抗的测试：线路终端开路（即R\(_{k}\)=∞），在始端测量输入阻抗，称为地下线在终端开路时的输入阻抗，简称地下线的开路阻抗Z∞；线路终端短路（即R\(_{k}\)=0），在始端测量输入阻抗，称为地下线在终端短路时始端的输入阻抗，简称地下线的短路阻抗Z0。

有了开路阻抗Z\(_{∞}\)和短路阻抗Z0，就可以根据下式求出地下线的特性阻抗Z\(_{c}\)的模数，

地下线是对称四端网络，其始端和终端的特性阻抗相同。

地下线的特性阻抗，在低频时阻抗值较大，随着频率的增高特性阻抗逐渐减小。但当高于某一频率后，特性阻抗等于某一数值（Z\(_{c}\)=\(\frac{\sqrt{L}}{C}\)）而不变了。在线路很长和频率很高时，地下线的特性阻抗、开路阻抗、短路阻抗大致相等，即Zc≈Z\(_{∞}\)≈Z0。改变振荡器的频率，可以测出地下线在各种频率下的开路阻抗和短路阻抗，从而可以计算出各种频率时的特性阻抗。

6.地下线衰耗的测量：在负载阻抗等于地下线终端的特性阻抗，且信号源内阻等于地下线始端的特性阻抗时测得的衰耗，称为线路的固有衰耗。固有衰耗又叫特性衰耗。

由于地下线不是工作在某一固定频率，而是工作在较宽的频带下，要使负载阻抗和信号源的内阻随着频率的改变来与地下线完全匹配是不可能的。因此有必要引用线路在工作情况下的衰耗概念，这种衰耗叫做工作衰耗。

当负载阻抗R\(_{k}\)等于信号源内阻r时，从图3可看出，线路从信号源获取的功率为

从图4又可以看出，在终端负载R\(_{k}\)上所取得的功率为P2=U\(^{2}\)\(_{2}\);Rk。则工作衰耗b可从下式算出：

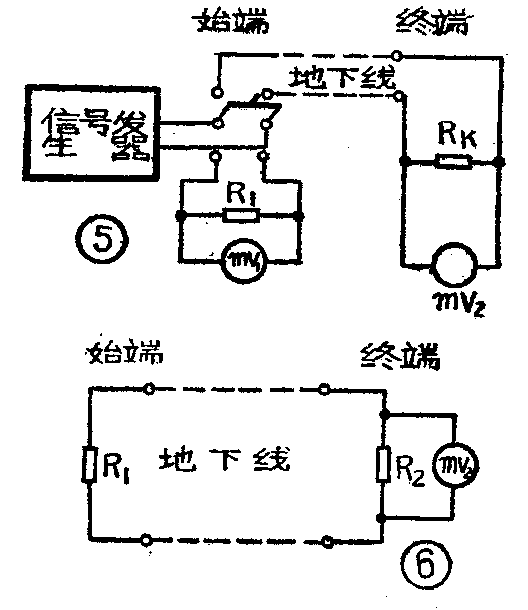
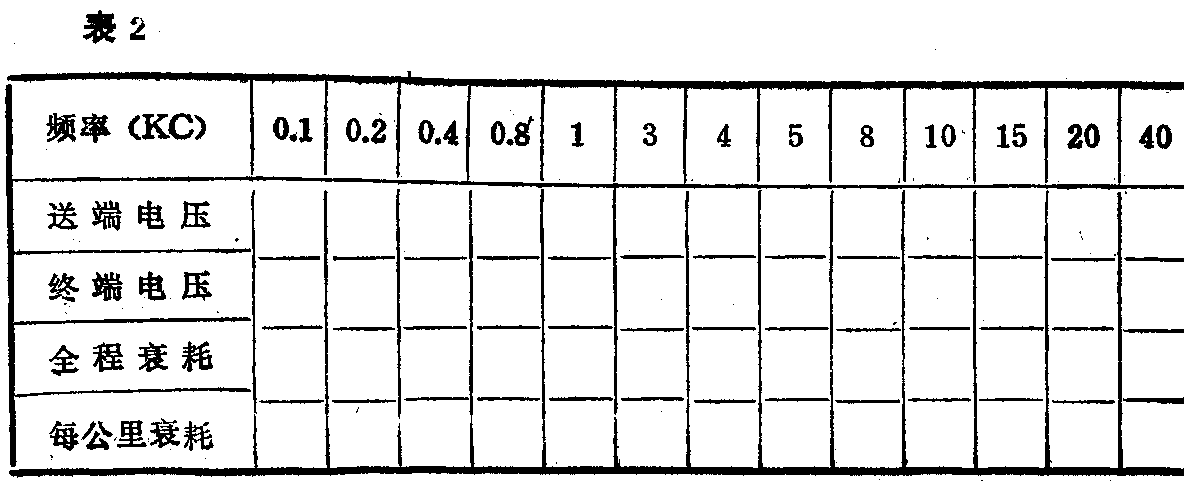
如果要测量在各种不同频率时的工作衰耗，可按图5接线法进行测量。首先接好仪器，使R\(_{k}\)=R1=r（r为振荡器内阻），调节振荡器到某一频率，开关扳向下方。然后调节振荡器输出，使其在5～15伏范围内，从毫伏表mV\(_{1}\)上可读出R1上的电压U\(_{1}\)，再把开关K扳向上方，在线路终端用毫伏表mV2读出R\(_{k}\)上的电压降U2，填入表2，根据下述公式就可计算出地下线在该频率时的工作衰耗。

改变振荡器的频率，重复上述作法，就可测出地下线在各种频率时的工作衰耗。用线路长度去除这些数据，就可以得出该地下线在各种频率时每公里的工作衰耗。根据这些数据，以横座标代表频率，纵座标代表每公里哀耗，可绘出该线路每公里的频率衰耗曲线。各频率的衰耗测量完毕后，关闭振荡器，拆除开关K，在线路上接上R\(_{1}\)，此时在终端的R2上测得的电压，即为线路的杂音电压（见图6）。

有些毫状表上有电平（分贝）刻度，测量时可以直接利用这种刻度，不必经过对数计算。

7．测试中应注意的事项：

①负载阻抗的选择。地下线工作在音频段时，可以5千赫时的特性阻抗值作为负载阻抗；工作在载频段时，以20千赫时的特性阻抗值作为负载阻抗。在测量衰耗大小时，终端的负载阻抗可按上述原则来决定。

②振荡器内阻的改变。测量地下线的衰耗时，振荡器的内阻不可能与上述负载阻抗相等，因此必须改变振荡器内阻。当内阻小于负载阻抗时，应在振荡器输出回路中串入一个电阻；当内阻大于负载阻抗时，应在振荡器输出端并接一个电阻。

当被测地下线是双线回路时，应使用平衡式输出的振荡器和毫伏表（或电平表）。如果它们不是平衡式的仪器，必须加装隔离变压器来达到平衡。(狄波初)