在无线电设备的调整、测试和维修等工作中,人们常常会遇到电阻器并联使用的情况。利用公式计算几个电阻的并联阻值比较麻烦,现介绍一种简易图解法,只需用一把直尺就可以较快地求得电阻器并联阻值。
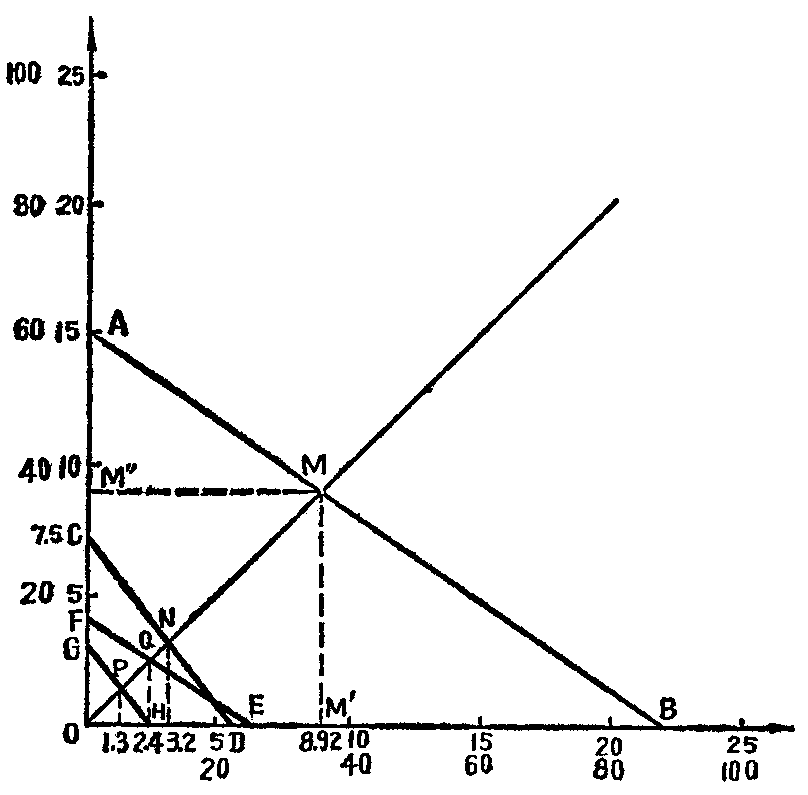
用一张小方格计算纸(每一小格为1平方毫米),画上直角座标轴和直角平分线(见图),横轴和纵轴按同样比例注上数字,表示电阻数值。阻值单位可用欧、千欧也可用兆欧,可根据需要自定,但横轴和纵轴上表示的阻值单位要一致。
下面介绍使用方法:
一、如果要求出阻值为15KΩ和22KΩ的两个电阻并联后的总阻值,只要将直尺连接纵轴上15(A点)与横轴上的22(B点)两点(纵、横轴上的数字调换一下也一样),则连线AB与角平分线交于M点。则M点在横轴(或纵轴)上的投影点M′(或M″)的相应阻值(8.92KΩ),即为15KΩ与22KΩ的并联总阻值。
二、如果需要用到一个3.2KΩ的电阻,想用已有的5.6KΩ电阻再并联一个电阻R\(_{2}\)来达到此值。利用图解法来求R2时:把横轴上5.6(D点)和角平分线上的N点(它在横轴上的投影为3.2)连接起来并延长后与纵轴相交C点,C点(7.5KΩ)就是要求的R\(_{2}\)数值。
三、假定有三个电阻器并联,可先找出其中两个的并联阻值,再与第三个按同法找出总的并联阻值。
例如有6Ω、4Ω、3Ω三个电阻并联,求并联阻值时,只要将直尺连接纵轴上的4(F点)与横轴上的6(E点)两点,则连线EF与角平分线相交于Q点。则Q点在横轴上的投影点的相应阻值为2.4Ω。再将直尺连接纵轴上的3(G点)与横轴上的2.4(H点),则连线GH与角平分线相交于P点,P点在横轴上的投影点的相应阻值为1.3Ω。
下面将图解原理作一证明:我们都知道两个电阻(R\(_{1}\)、R2)相并联后的阻值可用下列公式计算即R=\(\frac{R}{_{1}}\)R2R\(_{1}\)+R2。利用图解法来求时,线段OA、OB分别代表参加并联的两个电阻R\(_{1}\)和R2。只要证明OM′=OM″=OA·OB;OA+OB也就证明了OM′(或OM″)即是OA、OB两个电阻的并联总阻值。
因为M点在直角∠AOB的角平分线上,所以OM的水平投影和垂直投影显然相等。即OM′=OM″。又因OA·OB=2S\(_{△AOB}\)(S△AOB—表示三角形AOB的面积)
OM′·OA=OM″·OA=2S\(_{△AOM}\)…………(1)
OM′·OB=2S\(_{△BOM}\)…………………………(2)
把式(1)与式(2)相加得:
OM′(OA+OB)=2S\(_{△AOM}\)+2S△BOM=2S\(_{△AOB}\)
OM′=\(\frac{2S}{_{△AOB}}\)OA+OB=OA·OB;OA+OB
也就是说OM′(或OM″)就代表了OA·OB两个电阻的并联总阻值。
上述图解法也可用于串联电容求总容量。只要把两个轴所标的单位改一下即可。(黄明德、李介明、董清三)