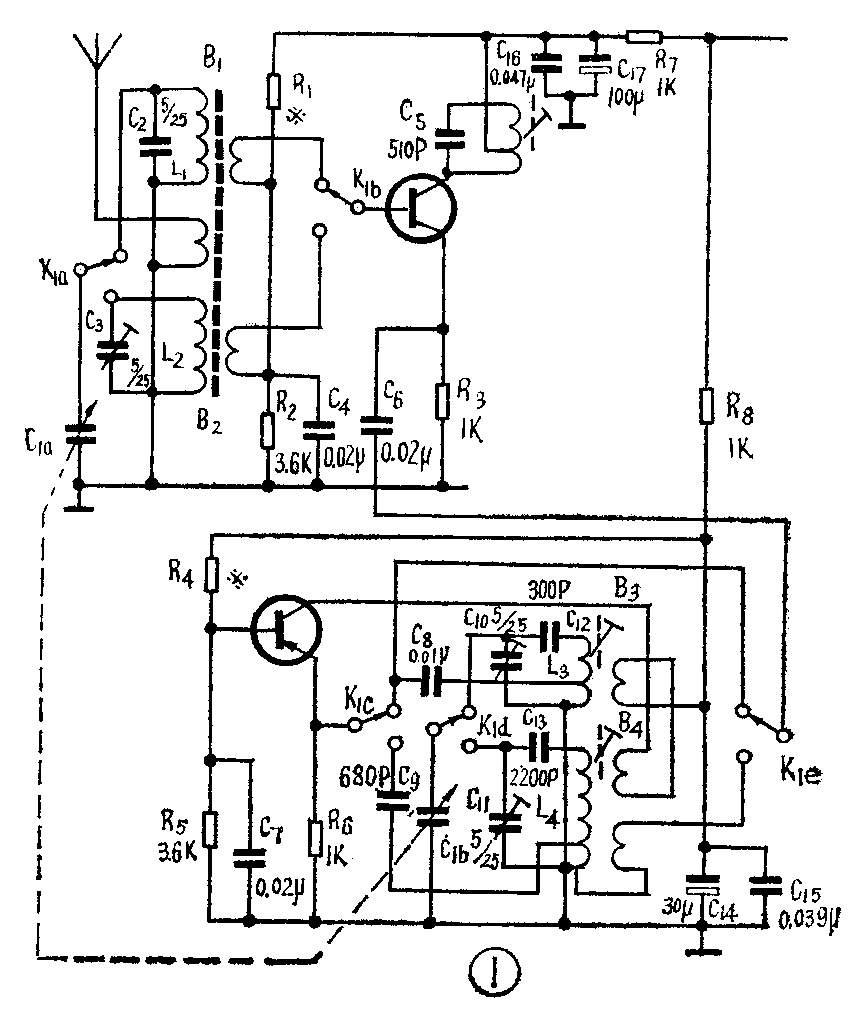
超外差收音机中装有双连可变电容器(简称双连),它是用来选择电台的。在收音机电路中,如图1所示,双连的其中一连接入输入回路,另一连接入本振回路。如果用其他规格的双连代换原来双连时,为使收音机工作正常,输入回路和本振回路中某些元件要变动。下面我们分输入回路和本振回路二部分来谈谈双连代换时的一些具体问题。
一、输入回路
如果要收听535~1605千赫(KHz)的电台信号,就必须使电路中(见图1)的C\(_{1a}\)从0°~180°覆盖这一频率范围。当C1a全部旋入时(0°),其容量最大为C\(_{1amax}\)。它与并联在回路上的补偿电容C2、杂散电容(包括线圈L\(_{1}\)自身电容、安装电容等等)一起,构成回路总电容C入max,并与L\(_{1}\)谐振在波段最低频率,即
f\(_{Smin}\)=\(\frac{1}{2π}\)\(\sqrt{L}\)1C\(_{入max}\)
当C\(_{1a}\)全部旋出时(180°),其容量最小为C1amin,这时回路总电容C\(_{入min}\)应与L1谐振在波段最高频率,即
f\(_{Smax}\)=\(\frac{1}{2π}\)\(\sqrt{L}\)1C\(_{入min}\)
通常我们称波段最高频率f\(_{Smax}\)与最低频率fSmin之比为覆盖系数K\(_{S}\)=fSmaxf\(_{Smin}\)。对输入回路来说,覆盖系数是由双连C1a、附加电容C\(_{2}\)'(包括C2和回路杂散电容)及电感L\(_{1}\)三个因素来满足的。C2'和L\(_{1}\)一经固定,就只能靠转动C1a来保证波段频率范围,因此C\(_{2}\)'和L1要根据C\(_{1a}\)的容量范围来确定。其中
C\(_{2}\)'=C1amax-K\(^{2}\)\(_{S}\)C1mainK\(_{S}\)2-1……①
L\(_{1}\)=\(\frac{25330}{f}\)\(^{2}\)Smin(C\(_{1amax}\)+C2')……②
式中C\(_{1a}\)、C2'的单位为pF(微微法),频率fS单位为MHz(兆赫),L\(_{1}\)单位为μH(微亨)。
譬如在中波段,接收频率范围要求为535~1605KHz,实际调整时应在频率范围的高低端留有一定的余量,通常把覆盖范围调整为525~1620KHz。这时覆盖系数K\(_{S中}\)=\(\frac{1620}{525}\)≈3.1。若用2×12/365pF双连,(即C1amax=365pF,C\(_{1amin}\)=12pF),用公式①可算出
C\(_{2}\)'=\(\frac{365-(3.1)}{^{2}}\)×12(3.1)2-1≈30pF,
如果估计杂散电容为15pF,则补偿电容应为C\(_{2}\)=30-15=15pF。将C2'代入公式②,可算出
L\(_{1}\)=\(\frac{25330}{(0.525)}\)\(^{2}\)(365+30)≈230μH。
若换用2×7/270pF双连,同样可计算得C\(_{2}\)'=24pF,则C2=24-15=9pF,L\(_{1}\)=320μH。
又如在短波段,接收频率范围要求为3.9~12MHz,也考虑到覆盖余量,实际应做到3.7~12.5MHz,则短波覆盖系数K\(_{S短}\)=12.53.7=3.38。若2×12/365pF双连,接公式①可算出
C\(_{3}\)'=\(\frac{365-(3.38)}{^{2}}\)×12(3.38)2-1=22pF,
由于短波输入线圈的自身电容较小,故杂散电容小于中波段,可估计杂散电容为12pF,则补偿电容C\(_{3}\)=22-12=10pF。同样可算得
L\(_{3}\)=\(\frac{25330}{(3.7)}\)\(^{2}\)(365+22)≈4.8μH。
若换用2×7/270pF双连,算得C\(_{3}\)'=18pF,则C3=18-12=6pF,这时L\(_{3}\)≈6.4μH。
为了补偿杂散电容估计的出入,补偿电容C\(_{2}\)、C3一般都采用5/20pF或5/25pF瓷介微调电容。由于C\(_{2}\)、C3的微调范围较大,故有时可不去算它,而直接计算输入线圈电感,即
L\(_{1}\)=\(\frac{25330×(K}{^{2}}\)S-1)f2\(_{Smax}\)(C1amax-C\(_{1amin}\))…………③
中波输入线圈L\(_{1}\),通常是用多股丝包线密绕在RK4(旧型号为MXO—400)磁棒上。同一个线圈套在不同尺寸的磁棒上,其电感量不一样。譬如将一个线圈分别套入φ10×100、120、140、160、180、200mm等不同长度的磁棒上,其有磁心时的电感量与空心电感量之比,是7、8、9、10、11、12倍,磁棒越长,线圈电感量越大。另外当线圈由中间向两端移动时,其电感量变小,磁棒越长变化越大。但线圈的高频损耗却中间最大,两端最小(即所谓线圈品质因素Q值是中间低、两端高)。因而为了减小线圈高频损耗,提高收音机灵敏度,中波输入线圈总是用多股线分成二段、三段甚至四段绕制,分别套入磁棒两端串接起来。这种绕法,圈数要多一些,但总的效果是好多了。以φ10×200mm圆磁棒为例,要绕制配用2×12/365pF双连的输入线圈,可用28×0.07mm丝包线分三段绕(也可用7×0.07丝包线,股数越多,线圈Q值越高),磁棒一端绕二段(20圈+20圈),另一端绕20圈,然后串接起来(共60圈)。若换用2×7/270pF双连,则圈数要增加到74圈,即一端绕(25+25)圈,另一端绕24圈。
短波输入线圈L\(_{2}\),应考虑到尽量减小杂散电容、提高线圈Q值,因而总是用较粗的漆包线或镀银铜线间绕在R60(旧型号为NXO—60)磁棒上,一般不分段绕制。短波磁棒导磁率虽低,但高频损耗却小多了。以φ10×160mm磁棒为例,若短波段频率范围为3.9~12MHz,要配用2×12/365pF双连,则可用φ0.8镀银线间绕8.5圈,若换用2×7/270pF双连,就要增加到13圈。
综上所述,在波段覆盖已定的情况下,无论对中波段还是短波段,如果换用容量不同的双连,与其配用的输入线圈电感量就要重新计算,然后按电感量的要求去绕制线圈。由于磁性材料的性能很难保证一致,线圈绕制方法(分成几段)也不一样,因而圈数很难由计算确定,需要在实际调试时确定。绕制时可根据磁棒长短适当多绕点,在调整中若将线圈移到磁棒边端还嫌电感大,则可适当拆几圈。
二、本振回路
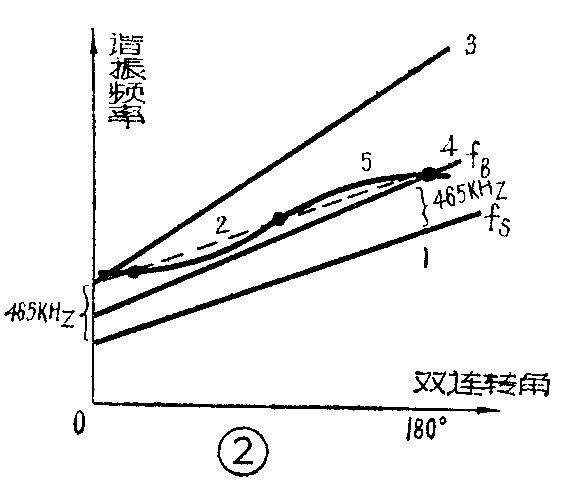
在输入回路中,双连电容的输入连C\(_{1a}\)转动角度和它所接收的信号频率fS的关系如图2斜线①所示;而和信号频率对应的本振频率f\(_{B}\)均应高出一个中频fZ,这就要求本振频率和双连振荡连C\(_{1b}\)的转动角度的关系如图2平行虚线②(即所谓理想跟踪线)。在中波段,本振频率fB的范围应为(525+465)~(1620+465)KHz,即其覆盖系数为K\(_{B中}\)=2805990≈2.1。可见本振覆盖系数比输入回路要小得多。
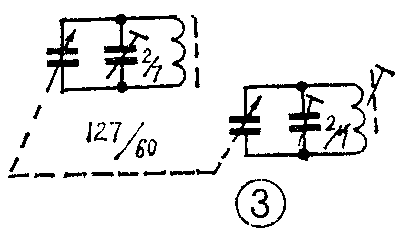
若采用如图3所示127/60pF差容双连,其角度容量大的那一连(4.5~127pF)用在输入回路,以满足K\(_{S中}\)=3.1的要求,而角度容量小的一连(3.5~60pF),则用在本振回路,恰好满足KB中=2.1的要求。因此,本振回路的结构与输入回路相同,本振线圈的电感计算就同输入回路一样,可用公式③,即得
L\(_{2}\)=\(\frac{25330×(2.1}{^{2}}\)-1)(2.085)2(60-3.5)≈350μH
故可选用LTF—1—1型中振线圈(黑色磁帽),其电感量340~420μH可调。由于差容双连的角度容量是接中波段的频率范围专门制作的,故不宜用于两波段的收音机中。
若采用如图1所示等容双连,C\(_{1a}\)—C1b,其角度容量相等,本振回路如不采取措施,就会有与输入回路相同的覆盖系数,即K\(_{B}\)=KS。但由于本振频率比信号频率高,故对于同一双连转角,本振线圈L\(_{3}\)的电感量总是比输入线圈L1小的,如果使本振回路的f\(_{B低}\)在波段低端比输入回路fS低高一个中频,即f\(_{B低}\)=fS低+465KHz(亦即所谓准确跟踪)则当C\(_{1b}\)从0°到180°,本振频率的变化就如图2斜线③所示,频率越高,跟踪越差。反之,若在高端准确跟踪,又会得到如图2外线④所示的变化,即频率越低,跟踪越差。怎么办?可采用附加电容的办法。如图1电路中,在本振回路串入一个较大容量的垫整电容C12(短波段为C\(_{13}\))。并联一个可谓的补偿电容C10(短波为C\(_{11}\))。在低端频率,较大容量的C12与C\(_{1b}\)串联,使回路总电容大大减小,振荡频率就升高,随着C1b的旋出,C\(_{1b}\)容量逐渐减小,C12的串联作用也就越来越不显著,但补偿电容C\(_{1}\)0的作用却越来越显著,到C1b完全旋出时,可能使C\(_{1}\)0≥Clbmin,C\(_{1}\)0的并联作用就最显著,使回路总电容加大,振荡频率变低。由于垫整电容C12的串联作用和补偿电容C\(_{1}\)0的并联作用,就使本振频率出现如图2曲线⑤那样“S”形变化,低端频率被拉上去,高端频率被压下来,这样本振回路的覆盖系数就被压缩了。“S”曲线与理想跟踪线②相交三点,在中波段,为使整个波段内灵敏度较为均匀,大都选取600、1000、1500KHz三点,作为准确跟踪点。其它各点则稍差一些,但从“S”曲线来看,比起斜线③、④来是大为改善了。
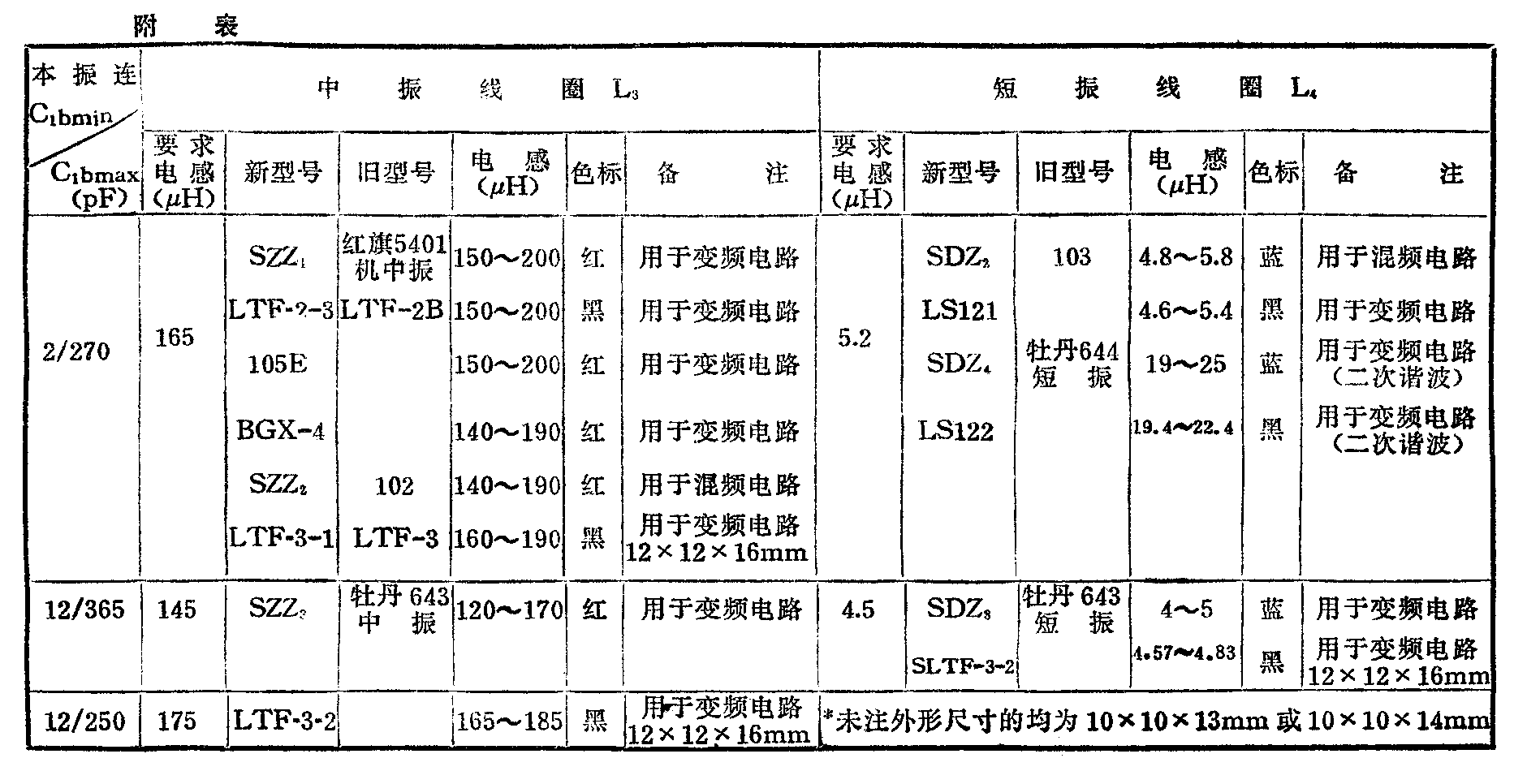
统调计算可知,在图1电路中,要满足中波段在上述三点作准确跟踪,对于用2×7/270pF双连,要求本振线圈电感量为L\(_{3}\)=165μH,若换用2×12/365pF双连,则要求L3=145μH。在4~12MHz短波段,要满足在4.8、12MHz三点准确跟踪,对于用2±7/270pF双连,要求L\(_{4}\)=5.2μH,若是采用二次谐波作本振的话,本振的基波fB=2.1825~6.2325MHz,用它的二次谐波为2f\(_{B}\)=2×(2.1825~6.2325)=4.465~12.465MHz,这种本振回路,其基波频率较低,因此本振线圈电感要求较大,其L4=22μH。如果换用2×12/365pF双连,要求L\(_{4}\)=4.6μH,采用二次谐波,则要求L4=15μH。配用不同规格双连的本振线圈型号、规格可见附表所示。
垫整电容C\(_{12}\)的大小与中间跟踪点有关。在中波段,只要取C12=C\(_{1bmax}\)或稍大些,就可满足在中间点fS中=1000KHz附近准确跟踪。譬如用2×7/270pF双连,可取C\(_{12}\)=270~300pF,若用2×12/365pF双连,则可取C12=360~390pF。在短波段,由于本振覆盖系数同输入回路相差不多,故对上述等容双连来说,一般取C\(_{13}\)=1800~2400pF。
补偿电容C\(_{1}\)0,C11,亦同输入回路一样,可采用5/25pF或7/30pF的瓷介微调电容。由于本振覆盖范围一经调定,不会再动,因此C\(_{1}\)0、C11通常都采用上述容量范围的拉线微调电容。只要C\(_{1}\)0、Cll容量范围足够,本振覆盖系数就能得到满足。
综上所述,换用双连时,本振回路的垫整电容和本振线圈均应根据双连规格作相应变动,本振线圈只有在调得到所需电感值的时候才可代用。换用双连对耦合电容C\(_{8}\)、C9毫无影响,可以不动。如图1电路中C\(_{8}\)可取4700pF~0.01μF,C9可取240~680pF。(金国钧)