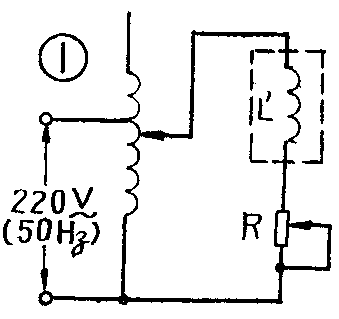
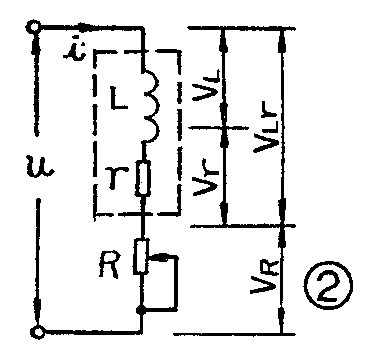
测量电路如图1所示,图中R为可调电阻。大家知道,电感元件中总是有直流电阻的,用r表示,因此可以把实际电感L′等效成一个纯电感L和电阻r相串联,如图2。利用万用表可以很方便地测出L′两端和R两端的电压降V\(_{Lr}\)、VR,也可以测出直流电阻r。
因为 V\(_{r}\)=I·r=VRR·r
所以 V\(_{L}\)=\(\sqrt{V}\)\(^{2}\)Lr-V2\(_{r}\)
=\(\sqrt{V}\)\(^{2}\)\(_{Lr}\)-(VRR)2·r\(^{2}\)
=V\(_{R}\)·\(\sqrt{V}\)LrV\(_{R}\))\(^{2}\)-(r;R)2
=2πfL·\(\frac{V}{_{R}}\)R
=100πL·\(\frac{V}{_{R}}\)R
所以
L=\(\frac{R}{100π}\)·\(\sqrt{V}\)\(_{Lr}\);VR)\(^{2}\)-(\(\frac{r}{R}\))2…①
上式计算L值还太麻烦。测量时我们选择R》r,即(\(\frac{V}{_{Lr}}\)VR)\(^{2}\)》(r;R)2,①式则可简化为
L=\(\frac{R}{100π}\)·V\(_{Lr}\);VR……②
如果选择R=3140欧,且调节测量电压使V\(_{R}\)=10伏,则②式进一步简化为
L=V\(_{Lr}\)……③
③式说明,电感元件两端的电压降读数V\(_{Lr}\)即代表了它的L值。若VLr单位为“伏”,则L的单位为亨。在L值小于1亨时,为了提高V\(_{Lr}\)读数的准确性,VR可以取100伏,这时③式变为:
L=0.1V\(_{Lr}\)……④
由上可见,利用③式测量电感元件电感量的精确程度决定于r与R比值的大小。理论上可以证明,对于0.7亨利以上的电感元件,如果满足关系式\(\frac{r}{R}\)≤1;100,测量误差则小于1%。(郑浩、魏华)