运算放大器实质上是一个加上了深度负反馈的高增益直流放大器。“运算放大器”首先应用于模拟计算机领域,可以完成微分、积分、加减乘除等数学运算,所以有运算放大器之称。目前运算放大器的应用已远远超出模拟计算机领域,在测量、控制、通信、信号变换等方面获得广泛应用,在仪器仪表中日益多见。常用的有5G922(8FC1),8FC2,4E312,4E304,BG303,BG305,5G23,5G24,FC3等型号。
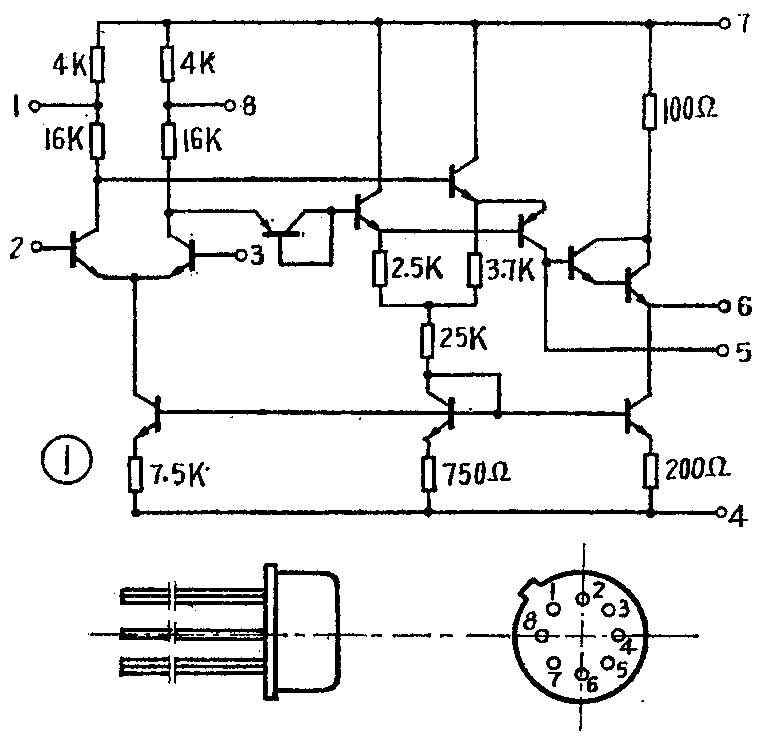
图1是运算放大器5G23的电路图和外形图。实际上,对运算放大器的使用者来说,重要的是了解放大器的性能参数及如何选择外部反馈元件。因此,本文着重介绍运算放大器的性能参数,并简述其运算功能。
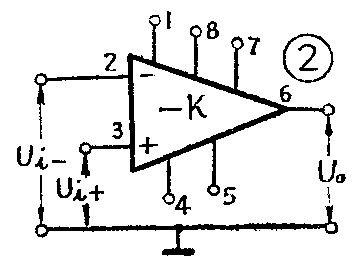
在工程电路中,常常不画它的线路图,而以图2所示的符号来表示,其中“2”端的输入信号和输出反相,标以“-”号,称为反相输入端;“3”端输入信号和输出同相,标以“+”号,称为同相输入端;“6”端为输出端;“7”、“4”端为电源端子;“1”、“5”、“8”端子为外接端子,要看具体应用电路而定。不同型号的运算放大器的端子的连接也不相同,要注意查阅有关说明资料。
运算放大器的主要性能参数
1.输入失调电压U\(_{os}\)。理想的运算放大器,当输入电压Ui+=U\(_{i}\)-=0时,输出应为U0=0。但在实际的运算放大器中,由于制造中元件参数的离散性等原因,当U\(_{i}\)+=Ui-=0时,U\(_{0}\)≠0。反过来说,如果要输出电压U0=0,必须在输入端加一个很小的补偿电压U\(_{os}\),这电压称为输入失调电压。显然,它愈小表示组件性能愈好。Uos一般在毫伏数量级。
2.输入失调电流I\(_{os}\)。它是指输入信号为零时,两个输入端静态输入偏置电流之差。同样,Ios愈小表示性能愈好,它一般在零点几微安至微安数量级。
3.输人偏置电流I\(_{ib}\)。指当输入信号为零时,两个输入端静态基极电流的平均值。其大小主要和电路中第一级晶体管的性能有关。也希望它愈小愈好,一般在微安数量级。
4.开环电压增益K。指在没有外加反馈环路、工作在低频时运算放大器的电压增益。在图2中“2”端和“3”端分别加上信号U\(_{i}\)-和Ui+时,“6”端输出为U\(_{0}\),输出和输入信号的关系是:
U\(_{0}\)=K(Ui+-U\(_{i}\)-)……(1)
运算放大器很少开环使用,因此开环增益K主要用来说明运算精度。K越大并越稳定,运算精度也就越高。如中增益运算放大器5G23和FC3的开环增益K均可达10万倍。
5.共模抑制比CMRR。理想的运算放大器,对于共模输入电压,不会产生输出电压,也就是说,只要|U\(_{i}\)+|=|Ui-|,就有U\(_{0}\)=0。但在实际的运算放大器中,同相输入端和反相输入端的电压增益不可能完全相同,因此不能完全抵消共模输入电压。
如果我们在两个输入端加上共模输入电压|U\(_{i}\)+|=|Ui-|=U\(_{iCM}\),而输出为UoCM,则称K\(_{CM}\)=UoCM;U\(_{iCM}\)为共模电压增益。与此对应,前面所述的电压增益K就称为差模电压增益。二者之比用分贝单位来表示,即
CMRR(dB)=201og\(\frac{K}{K}\)\(_{CM}\)(dB)
称为共模抑制比。它标志运算放大器对共模信号抑制能力的好坏。希望CMRR愈大愈好,一般应在80dB以上。
6.输入阻抗Z\(_{i}\)和输出阻抗Z0。在实际的运算放大器中,两个输入端之间电压的变化(ΔU\(_{i}\)+-ΔUi-)将引起输入电流的变化ΔI\(_{i}\),两者之比称为输入阻抗。即:
Z\(_{i}\)=ΔUi+-ΔU\(_{i}\)-ΔIi
希望输入阻抗越大越好,理想运算放大器输入阻抗为无限大,一般从几百千欧至几兆欧。
输出电流的变化将引起输出电压变化,二者之比称为输出阻抗
Z\(_{0}\)=ΔU0ΔI\(_{0}\)
希望输出阻抗越小越好。理想运算放大器输出阻抗为零,实际的数值一般在几百欧以内。
7.温度漂移。输入失调电压和输入失调电流随温度变化而改变的现象称为温度漂移,温度漂移愈小,运算放大器的稳定性愈高。
8.共模输入范围。运算放大器对共模信号具有抑制的性能。但是这个性能只是在输入共模电压在一定范围内时才具备。如果超过这个电压范围,运算放大器的共模抑制比大大降低,输出将出现严重畸变,甚至造成损坏。
9.最大输出电压和最大输出电流。能使输出电压与输入电压保持不失真关系的最大输出电压,叫做运算放大器的最大输出电压。这时能给出的最大输出电流,叫做运算放大器的最大输出电流。
由上可见,集成运算放大器具有开环增益高、输入阻抗高、输出阻抗低、漂移小、体积小、可靠性高等基本特点,因此,它已成为一种通用器件,广泛而灵活地应用于各个领域。
加上反馈网络后的运算放大器
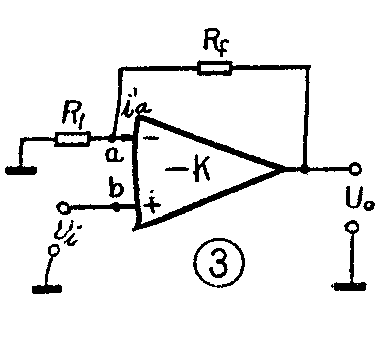
图3是加上反馈网络接成同相输入的反馈放大器。图中自同相输入端输入电压U\(_{i}\),自输出端至反相输入端外加负反馈电阻Rf。由于理想运算放大器的输入阻抗无限大,因此i′\(_{a}\)=0,而a点的电位即为
U\(_{a}\)=R1R\(_{1}\)+RfU\(_{0}\)
根据(1)式可以列出
U\(_{0}\)=K〔Ui-\(\frac{R}{_{1}}\)R1+R\(_{f}\)U0〕
由此,
U\(_{0}\)=〔R1+R\(_{f}\)R1〕·〔1;1+\(\frac{R}{_{1}}\)+RfKR\(_{1}\)〕·Ui
当K很大时,
U\(_{0}\)≈R1+R\(_{f}\)R1U\(_{i}\)
或闭环增益K\(_{f}\)=U0U\(_{i}\)=R1+R\(_{f}\);R1,也就是说,只要K足够大,输出电压与输入电压成简单倍数关系,闭环增益K\(_{f}\)只决定于电阻比R1+R\(_{f}\)R1,而与其它无关。这里也可以看到,只要K足够大,电阻R\(_{1}\)和Rf较精确和稳定,就可以达到很高的运算精度。
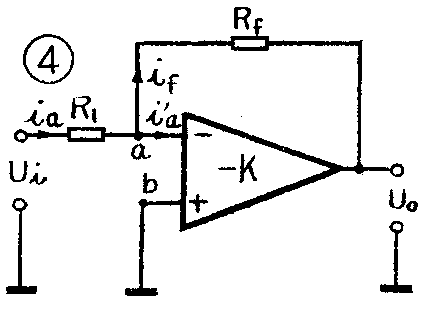
图4是接成反相输入的反馈放大器。由于i′\(_{a}\)=0,所以ia=i\(_{f}\),即
式中U\(_{a}\)是a点电位,a点是反馈电压加到输入端的那个点,通常称为相加点。此时Ui+=0,根据式(1)得U\(_{0}\)=-KUa,如果K无限大,则相加点电位\(_{U}\)a→0,也就是说,这点处于“不接地的地电位”,因此,通常称它“虚地”。可以证明,当K很大时,输出电压与输入电压的关系为:
U\(_{0}\)=-RfR\(_{1}\)Ui
或 K\(_{f}\)=U0U\(_{i}\)=-Rf;R\(_{1}\)
负号表示输出电压与输入电压相位相反。只要K足够大,这个放大器的闭环增益K\(_{f}\)只决定于电阻比RfR\(_{1}\)而与其它无关。运算精度同样决定于K。
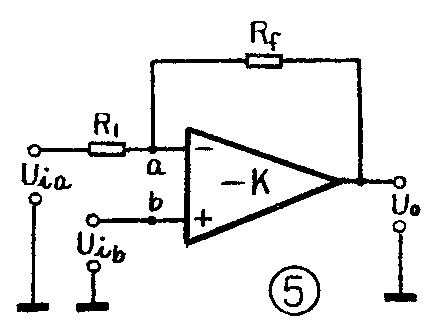
当然,也可以如图5那样将运算放大器连接成差动输入的反馈放大器。可以证明,当K足够大时,输出电压与输入电压的关系为:
U\(_{0}\)=R1+R\(_{f}\)R1U\(_{ib}\)-Rf;R\(_{1}\)Uia
通过以上的分析可以看到,运用运算放大器,可以很方便地制成放大倍数可以精确控制的放大器。
运算放大器的运算功能
加上适当的负反馈后,由于输出电压与输入电压之间存在着较精确的比例关系,用运算放大器可以实现常见的数学运算。为了简化分析,我们仍然假设所讨论的是理想运算放大器。只要运用得当,这些结论对于实际的运算放大器也是正确的。
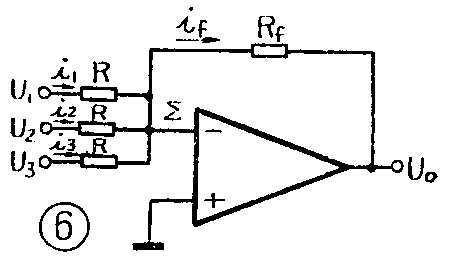
1.加法运算:图6是一个反相加法器的原理图,Σ点为虚地,输入信号U\(_{1}\)、U2、U\(_{3}\)(输入信号可以很多个)分别经电阻R接在反相输入端,由于运算放大器输入阻抗为无限大,因此
i\(_{f}\)=i1+\(_{i}\)2+i3
即-U\(_{0}\)Rf=U\(_{1}\);R+U2R+U\(_{3}\);R
也就是 -U\(_{0}\)=RfR(U\(_{1}\)+U2+U\(_{3}\))
式中负号表示输入输出反相,如取R\(_{f}\)=R,则-U0=U\(_{1}\)+U2+U\(_{3}\),成为一个加法器。
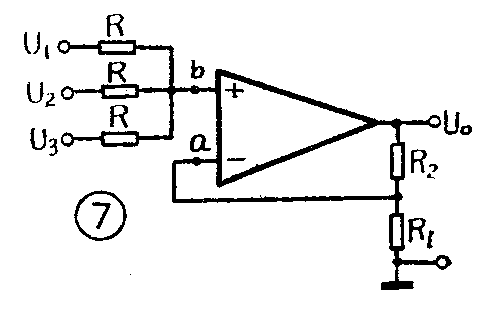
图7是接成同相加法器的原理图,对于节点b的电流可写成
即 U\(_{1}\)+U2+……+U\(_{n}\)=nUb
但因 U\(_{a}\)=Ub=U\(_{0}\)·R1R\(_{1}\)+R2
所以 U\(_{0}\)=(1+R2R\(_{1}\))1;n·(U1+U\(_{2}\)+……+Un)
适当选择R\(_{1}\)及R2,即可实现加法运算。例如n=2,就选择R\(_{1}\)=R2。
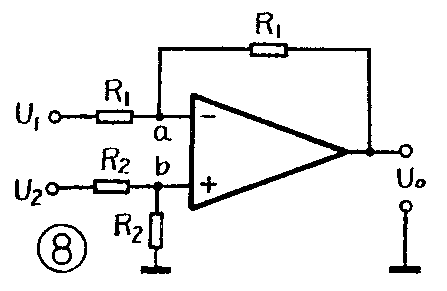
2.减法运算:减法运算原理图见图8。由图可见,
U\(_{b}\)=U22,并且U\(_{1}\)-Ua;R\(_{1}\)=Ua-U\(_{0}\)R1,
即 U\(_{a}\)=\(\frac{1}{2}\)(U1+U\(_{0}\))
又由于 U\(_{2}\)=Ub=\(\frac{U}{_{2}}\)2
即\(\frac{U}{_{2}}\)2=1;2(U1+U\(_{0}\))
所以 U\(_{0}\)=U2-U\(_{1}\)
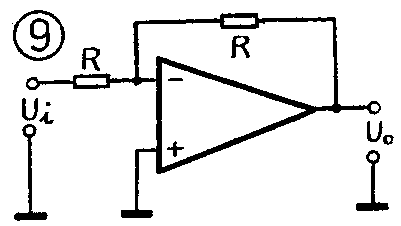
3.反相运算:如图9即实现倒相运算U\(_{0}\)=-Ui。
4.比例运算:图3就是同相输入比例器,U\(_{0}\)=R1+R\(_{2}\)R1U\(_{i}\)。图4就是反相输入比例器,U0=-R\(_{f}\);RUi。
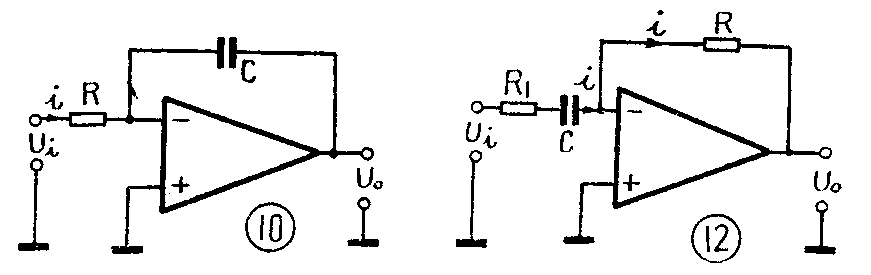
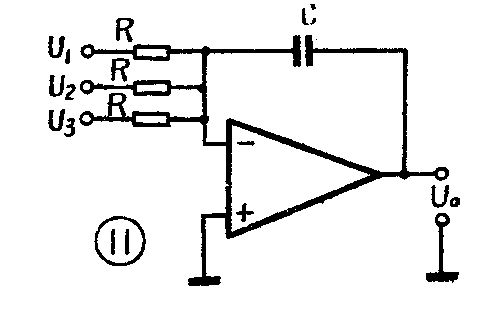
5.积分和微分运算:以电容C作为反馈元件,就可以制成简单的积分器(图10)。在这个电路中输出电压正比于输入电压对时间的积分。如果同时输入几个信号U\(_{1}\)、U2、U\(_{3}\),如图11所示,可以构成积分求和器。如按图12连接,即成微分器,它的输出电压正比于输入电压对时间的微分。
除此而外,运算放大器还能进行求解微分方程、求对数运算、求反函数运算及乘方开方运算等等。
运算放大器的其它应用举例
运算放大器除了能进行上述数学运算外,已经越来越多地用来组合成各种类型的放大器、振荡器、转换器、滤波器、恒流源、恒压源等等。下面举几个实例。
1.将毫安表改为微安表
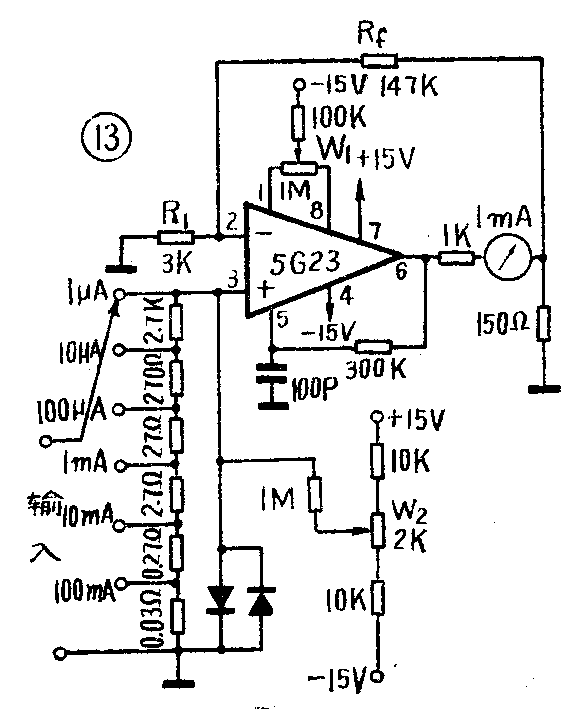
这是将运算放大器用于同相放大的一个实例。图13是测量电流的线路,由图可见,无论从那一档输入满度电流,在“3”端都产生3mV的输入电压,则输出电压应为:
U\(_{0}\)=Rf+R\(_{1}\)R1U\(_{i}\)=147KΩ+3KΩ;3KΩ×3mV=150mV
这是运算放大器输出端在150Ω电阻上的压降。由此可见,流过毫安表的电流应为\(\frac{150mV}{150Ω}\)=1mA,恰为满度值。
这里,1KΩ电阻为输出电路保护电阻,W\(_{1}\)电位器用于调零,“5”、“6”间所接的300KΩ电阻及“5”、“地”间的100pf电容均为外接补偿元件,W2电位器用于外加偏流补偿。
2.多谐振荡器
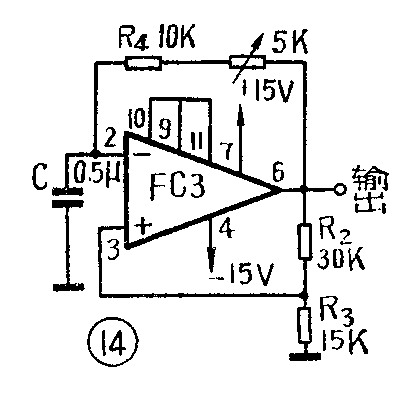
图14是用一个运算放大器FC3构成的简单的自激多谐振荡器,可以产生连续的方波。输出正、负电压近似等于正、负电源电压V\(_{+}\)和V-。如果在某瞬间输出电压等于V\(_{+}\),那么在“3”端电压则为V+·\(\frac{R}{_{3}}\)R2+R\(_{3}\),“2”端上的电压以指数形式接近V+,时间常数决定于R\(_{4}\)·C,当它超过“3”端电压的瞬间,输出就向V-反转,这时“3”端电压为V\(_{-}\)·R3;R\(_{2}\)+R3,而输出电压又通过R\(_{4}\)对C充电,使“2”端电压变化,当“2”端电压到达V-·\(\frac{R}{_{3}}\)R2+R\(_{3}\)时,又迅速翻转,使输出电压回到V+。这样周而复始,输出端即获得方波。本例方波频率在1千赫左右。
3.线性检波电路
图15是用运算放大器5G23构成的理想的线性检波器。当输入U\(_{i}\)>0时,运放输出端A点为负电位,二极管D2导通、D\(_{1}\)截止,因此U0=0。
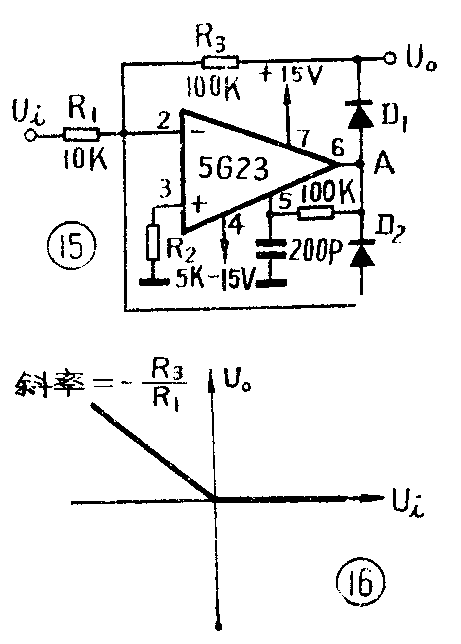
当U\(_{i}\)<0时,运放输出端A点为正电位,二极管D2截止、D\(_{1}\)导通,U0U\(_{i}\)=-R3;R\(_{1}\),因此该电路输出与输入呈比例关系,如图16所示,成为直线检波状态。
以上线路也可用其它型号的通用型集成运算放大器构成。(夏元复)