当热电偶冷端与热端有温度差时,在回路中便会产生热电势,这个热电势的大小、由热电偶的材料和冷、热端的温度差决定。根据这个原理,可以用热电偶来作温度计在用热电偶作温度计时,要对冷端温度随环境温度的变化进行补偿,才能使热电偶温度计的读数精确。下面介绍一种补偿电路,如图所示。
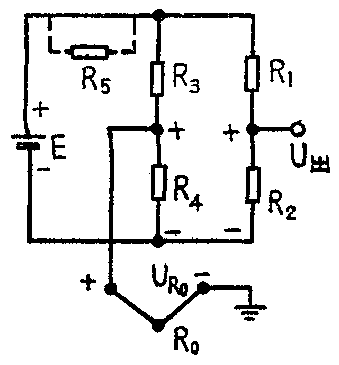
图中U\(_{R}\)0为热电势,U出为输出端对地的电位。从图U\(_{出}\)端子经R2、R\(_{4}\)、热电偶到地这一支路可看出:
U\(_{出}\)=UR2-U\(_{R4}\)+UR0……(1)
从式(1)可看出这个电路的工作原理,就是要利用(U\(_{R2}\)-UR4)随温度的变化来补偿U\(_{R}\)0因冷端温度变化而产生的变化。这就是说,我们可以适当选择电阻R2和R\(_{4}\)的材料和阻值,使在温度为0℃时,(UR20-U\(_{R4}\)0)=0,这时根据(1)式,可得
U\(_{出}\)=(UR20-U\(_{R4}\)0)+UR0=U\(_{R}\)0
在冷端温度为t℃时,U\(_{R}\)0变为URt,变化量为△U:
△U=U\(_{R}\)0-URt
如果这时(U\(_{R2t}\)-UR4t)能等于△U,则根据(1)式可得出:
U\(_{出}\)=UR2t-U\(_{R4t}\)+URt
由于(U\(_{R2t}\)-UR4t)=△U=U\(_{R}\)0-URt,所以在t℃时
U\(_{出}\)=△U+URt=U\(_{R}\)0-URt+U\(_{R}\)=UR0
因此,U\(_{出}\)可保持不变,达到了补偿目的。
怎样选择电阻R\(_{2}\)和R4呢?先列出几个式子:
从图中电源电压V\(_{E}\)的分压电路可得
U\(_{R2}\)=R2R\(_{1}\)+R2V\(_{E}\)……(2)
U\(_{R4}\)=R4R\(_{3}\)+R4V\(_{E}\)……(3)
在规定使用温度范围内,热电势的变化是与温度成正比的,即
式中t为温度变化量,K为比例常数,视热电偶材料而定,我们选用φ0.3毫米的镍铬—镍铝热电偶,它的K=40μV/℃。上式也可写成
U\(_{R}\)0-URt=Kt……(4)
上面已谈到,U\(_{R}\)0-URt=△U=U\(_{R2t}\)-UR4t,所以可得
U\(_{R2t}\)-UR4t=Kt……(5)
把在t℃时的(2)(3)两式代入(5)式,得
取R\(_{1}\)》R2及R\(_{3}\)》R4,上式可简化为
现在,我们就可根据式(6)来求R\(_{2}\)了。我们选用钢丝作R2,它的温度系数为α=4.28×10\(^{-}\)3/℃;用锰—铜丝作R\(_{4}\),它的温度系数为10-6/℃。R4的温度系数很小,可以忽略不计,也就是说R\(_{4}\)的电阻数值在一定范围内可认为不随温度变化。
在t℃时:
R\(_{2t}\)=R20+αtR\(_{2}\)0
R\(_{4t}\)=R40
代入式(6),得
取R\(_{1}\)=R3,并取R\(_{2}\)与R4在0℃时的阻值相等,即取R\(_{2}\)0=R40。这样,上式就可简化为
求解R\(_{2}\)0可得:
R\(_{2}\)0=R1KαV\(_{E}\)……(7)
我们取V\(_{E}\)=6.2伏,R1(=R\(_{3}\))取为6.2K,并把上述α、K数值代入(7)式,可算出R20=9.36欧,也就是说R\(_{2}\)和R4在0℃时的电阻为9.36欧。
图中还有个电阻R\(_{5}\),它的数值为560欧,调整R5,可使R\(_{1}\)、R2等分压器上的V\(_{E}\)保持为6.2伏。R1、R\(_{3}\)、R5等电阻,可选用金属膜电阻。
这个电路在0°~45℃范围内,温度补偿误差小于1℃。(地仪)