电容器在电路中的作用

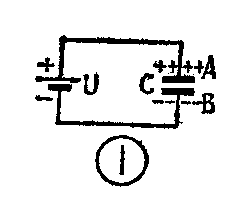
当我们把电容器接在直流电源上（见图1），与电源正极相连的极板A上的自由电子就要被电源正极吸引过去，A板由于缺少了电子而带上正电荷；电源负极将把自由电子推斥到与它相连的极板B上，使B极板多余了自由电子而带上负电荷。由于两极板距离很近，正负电荷就会互相吸引，即使把电源断开，电荷依然可以保存在极板上，也就是说，电容器储存了电荷。实验证明，电容器储存的电荷量Q与两极板间的电压U成正比。不同的电容器在加上相同的电压时，储存的电荷量也不相等。为了衡量一个电容器储存电荷的能力，我们把在单位电压作用下，每一极板所能储存的电荷量，叫做该电容器的电容量，用字母C表示，即

电容量的基本单位是法拉，简称法，用字母F表示。如果电容器两极板间加上1伏电压，能使每一极板储存1库仑的电荷，该电容器的电容量就等于1法拉。一般使用的电容器，容量都比法拉小得多，因此常用微法（μF）和微微法（PF）来计量。法拉，微法和微微法之间的换算关系为

充电与放电是电容器在各种电子电路中的最基本的运动形式。电容器在外加电压作用下，极板上积累电荷的过程，叫做电容器的充电。

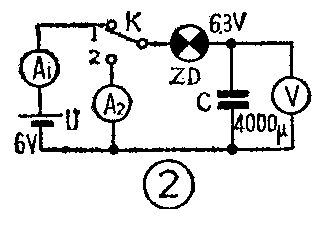
为了对电容器的充电过程有一个直观的印象，我们先来做一个简单的实验。将一个未充电的电容器C接入图2的电路中，当开关K合向1点时，电容器就被电源充电，可以看到灯泡ZD开始很亮，然后变暗，说明电路中充电电流在变化。从电流表A\(_{1}\)上可以观察到充电电流i充在逐渐减小，从电压表V上可以看到电容器两端电压u\(_{c}\)在逐渐上升，经过一定时间之后，灯泡不亮了，电流表的指针回到零位，电压表指示出电容器两端电压等于电源电压，即

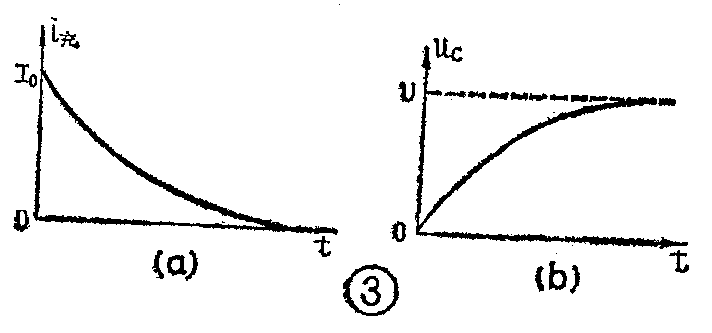
为什么电容器在充电过程中，电路中的电流会由大变小最后就没有电流了呢？这是因为当开关K扳向1点的瞬间，电容器上还没有电荷，即u\(_{c}\)=0，电源电压U全部加在灯泡ZD两端（灯泡的电阻为R），此时小灯泡两端电压uR=U为最大，因此，流过小灯泡的充电电流i\(_{充}\)也为最大，其值为

称为起始充电电流。充电开始后，电容器极板上电荷不断积累，电容器两端电压u\(_{c}\)也就随着不断升高，这时小灯泡两端电压将为uR=U-u\(_{c}\)，显然uR在不断减小，充电电流也逐渐下降。电流的减小，意味着电容器极板上电荷增长的速率在减小，因而电压u\(_{c}\)增加得愈来愈慢。最后，当uc上升到等于电源电压U时，由于它们的方向相反，达到了动态平衡，电容器极板上的电荷量不再变动，i\(_{充}\)=0，小灯泡也就不亮了。充电电流i充和电容器两端电压u\(_{c}\)随时间变化的曲线，分别如图3（a）和（b）所示。

以上实验表明，有电阻和电容组成的电路（又称RC电路）中，电容器的充电是需要经历一定的时间的，这段时间有多长呢？图4绘出了RC充电电路。显然，如果电容C一定，电阻R愈大，充电电流就会愈小，充电需要的时间也就愈长；如果电阻R一定，则充电电流的最大值I\(_{0}\)一定，电容C愈大，电容器充满电所需要的电荷也愈多，充电所需的时间也愈长。所以电容量C和电阻R是决定电容器充电快慢的两个主要因素，与电源电压无关。我们把电容C（法拉）与电阻R（欧姆）的乘积，称为RC充电回路的时间常数，用希腊字母τ表示，即

因此，充电的快慢，可以用时间常数τ充来衡量，τ充愈大，表示充电愈慢，u\(_{c}\)达到终止值所需的时间也就愈长。根据理论分析，容器从充电开始，经过τ充=RC（秒）这么长的时间，u\(_{c}\)正好上升到终止值U的63％，充电电流衰减到初始值I0的37％。表一给出了电容器两端电压u\(_{c}\)及充电电流i充随时间变化的情况。

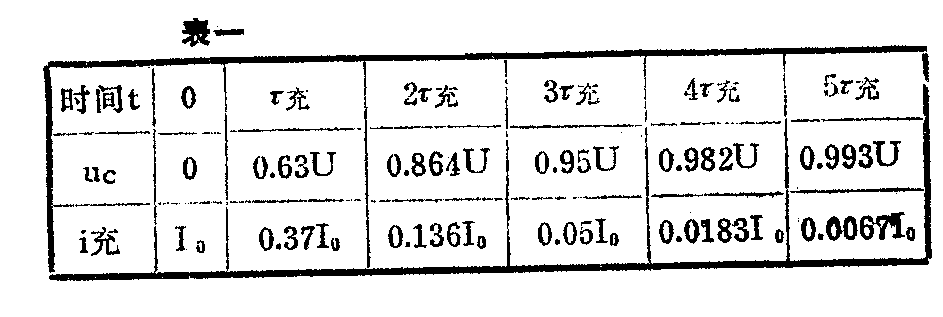
由表一可见，当t=5\(_{τ充}\)时，电容器上电压已充到接近电源电压U，而充电电流已经很小了，我们就认为充电过程经历5τ充的时间就能基本结束了。举例来说，图2的电路中，电容器的电容量C为4000μF，小灯泡ZD的电阻R为60Ω，则从开关K闭合瞬间到电容器充电完毕，大致需要t=5\(_{τ充}\)= 5×60×4000×10\(^{-}\)6=1.2秒。

为了了解放电过程，我们接着做图2的实验。当电容器C充好电后，我们把开关K扳向2点，可以看到小灯泡开始很亮，逐渐由亮变暗，最后不亮了。从电流表A\(_{2}\)可以看见电流由大变小，从电压表V可以看见电容器两端电压uc在逐渐下降，过一段时间之后，电压表及电流表的指针都回到零位，放电过程即告结束。

电容器放电过程的实质是什么呢？图5是RC放电电路。电容器充好电后，u\(_{c}\)=U，把电容器与电阻接成闭合回路瞬间，电容器就如同一个电源一样，在电压uc的推动下，自电子从它所在的负极板移出，流向带正电的正极板，与正电荷不断中和，在电路中就形成了放电电流。开关K闭合瞬间，电容器上的电压u\(_{c}\)最大，电路中的放电电流i放也最大，即

随着电容器极板上电荷的减少，u\(_{c}\)逐渐下降，放电电流i放也逐渐减小，直到电容器两极板上的电荷全部中和，u\(_{c}\)=0，电路中没有电压，电流也就等于零了。

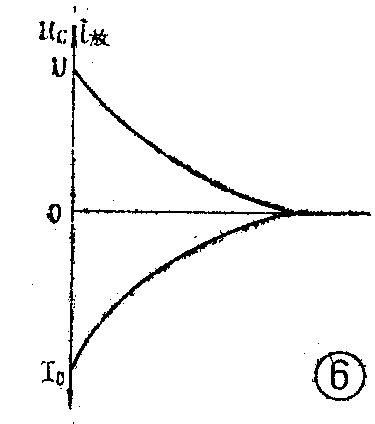
电容器放电过程中电流i\(_{放}\)和电压uc的变化情况，可用图6的曲线表示，由图中可以看到，放电时电流方向与充电时正好相反。电容器放电的快慢，同样由回路的电阻R和电容C的大小决定，R与C的乘积叫RC放电回路的时间常数，即

显然，τ\(_{放}\)愈大，放电过程所经历的时间愈长。根据理论分析，τ放相当于电容器两端的电压u\(_{c}\)和放电电流i放下降到初始值的37％所经过的时间。表二给出了u\(_{c}\)及τ放随时间变化的情况。

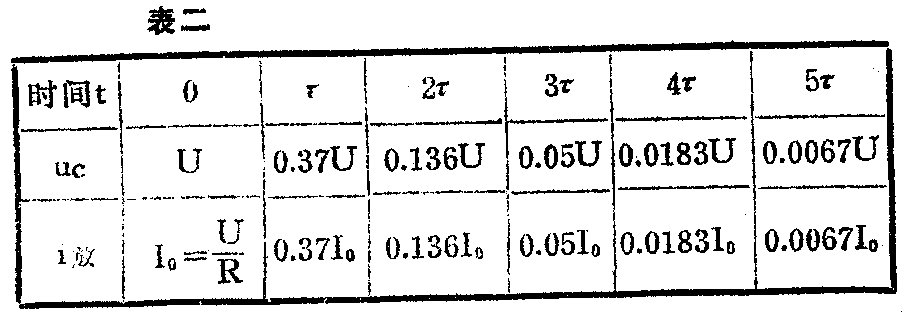
由表二可见，电容器自放电开始，经过大约5\(_{τ放}\)的时间，就可认为放电过程基本结束了。

综上所述，电容器的充电和放电都需要经历一定的时间，选择不同的回路电阻R和电容C，就能获得不同的充电和放电时间。在电子技术中，人们巧妙地利用电容器的充放电，组成定时电路、锯齿波产生电路、微分电路和积分电路等等。

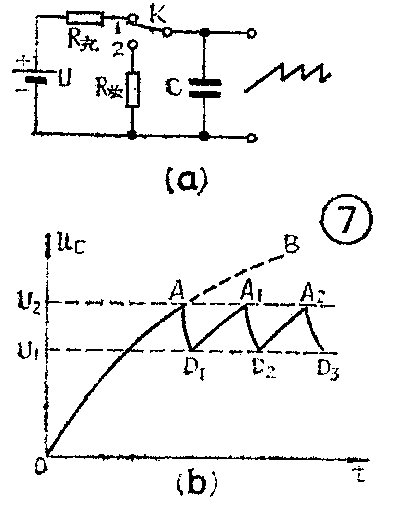
图7（a）是一个利用电容器的充电和放电来产生锯齿波电压的原理电路。开始时，开关K与1点接通，电源经很大的电阻R\(_{充}\)向电容器缓慢充电，电容器两端的电压uc按图7（b）的曲线OB增长，当u\(_{c}\)达到A点时（一般取曲线起始接近于直线的部分），uc=U\(_{2}\)，迅速把开关K扳向2点，此时电容器充电时积累的电荷便经很小的电阻R放放电，AD\(_{1}\)为放电曲线，放电时uc很快下降，当u\(_{c}\)下降到U1时，又把开关K扳向1点，电容器又按D\(_{1}\)A1的曲线充电，当充到u\(_{c}\)=U2时，又使其放电。以后如此周期性重复，便可在电容器两端得到锯齿波电压输出。必须指出，实际的锯齿波发生器中开关K采用的是电子开关。锯齿波电压被广泛应用于电视机和示波器等电子设备的扫描电路中。

上面已经谈到，电容器与小灯泡串联后接在直流电源上时，只是在电容器充电或放电的过渡过程中，即u\(_{c}\)变化的过程中，电路里才会出现电流，小灯泡才发光，当uc稳定不变时，电路中就没有电流，小灯泡也不亮，这就意味着电容器能起“隔直流”的作用。

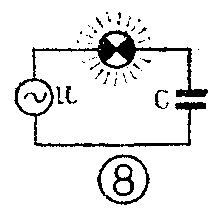
如果将电容器与小灯泡串联后接在交流电路中，如图⑧所示，则会看到小灯泡持续发光，电流表指示着电路中有连续的交流电流，人们习惯地说，电容器可以通过交流电，这又是怎么回事呢？

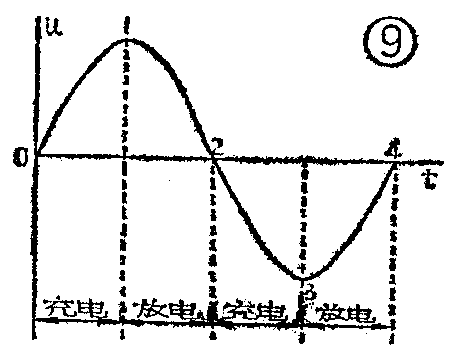
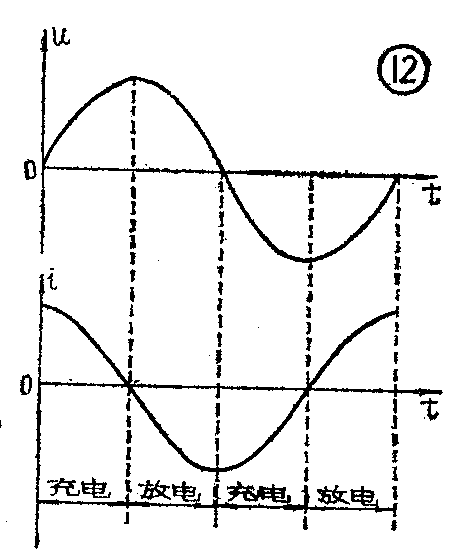
大家知道，交流电的大小和方向总是不断变化的，图9是正弦交流电压的波形图。我们把正弦波电压的一个周期分成四段进行分析。在0—1段，电压从零值向最大值增长，电容器上积累的电荷也不断增多，这时电容器处于充电状态，电路中流过充电电流。1—2段，电压从最大值向零值下降，电容器上积累的电荷也不断减少，这时电容器处于放电状态，电路中流过放电电流。当电压的极性反向时（图9中的2—3和3—4段）电容器就反方向充电和放电，电路里流过反方向的充电和放电电流。显而易见，由于交流电压每时每刻都在变化，电容器也就每时每刻都处于充电或放电状态，电路里也就相应地产生充电和放电电流，串联在电路中的小灯泡也就能持续发光了。

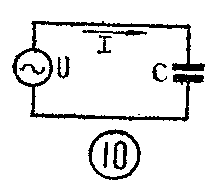
从以上分析可知，在带有电容器的交流电路中，电流不是真的能够通过电容器，而是由于电压的变化，引起电容器不停地充电和放电，才使电路中产生了电流。因此，图10所示的电容电路中的电流大小与电容器的电容量C和电压变化速率成正比，在实际计算中常用到以下的公式I=2πfCU式中：电压U与电流I都是交流电的有效值，2π=6.28是个常数，f是交流电的频率，C是电容量。上式可以写成大家熟悉的欧姆定律的形式

式中X\(_{c}\)=\(\frac{1}{2πfC}\)叫做交流电路的容抗，单位是欧姆。容抗大小与电容量C和频率f成反比。在带有电容的交流电路中，当电压一定时，容抗愈大，电流愈小，反之容抗愈小，电流愈大，因此容抗Xc是交流电路中的一种特殊阻力，这概念在分析电路时很重要。

为了进一步研究电容交流电路中电压与电流之间的相位关系，让我们更仔细地分析交流电压在一个周期时间内变化的情况。图11把交流电压的正弦曲线分为许多细小的相等的时间段。在0—1的时间内，电压的变化量等于a。在1—2的时间内，电压的变化量等于b。在2—3的时间内电压的变化量为C，余可类推。可以看出，电压从零值向最大值变化时，电压的变化速率——单位时间电压的变化量——是愈来愈小的，直至达到最大值时电压的变化速率趋近于零。电压继续由最大值向零值变化时，电压的变化速率则是愈来愈大的，到接近零值时，电压变化速率最大，在负半周内的变化情况与此相似。

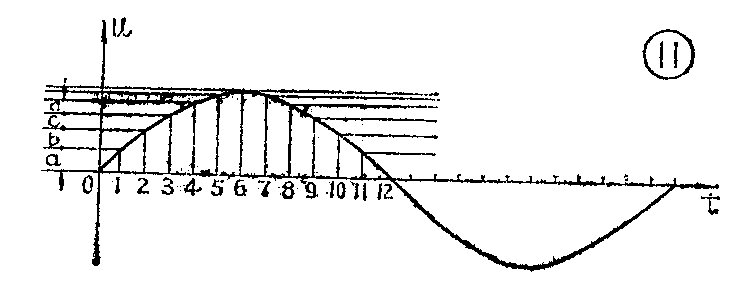
观察一周期中电压的变化情况可知，电压变化速率最快是在它接近零值时，而在到达最大值瞬间，电压变化速率等于零。当电路中电容量C一定时，由于电流的大小与电压的变化速率成正比，所以电压变化到零时，电流正好为最大值，电压变化到最大值时，电流却变到零，如图12所示。从图12还可以看到，电容器充电时，电压与电流方向相同；电容器放电时，电压与电流方向相反。显然，在接有电容器的交流电路中，电压和电流的变化步调是不一致的，从到达最大值的先后可以看出，电流超前电压四分之一周期，也就是说它们的相位差是四分之一周期。(宋东生)