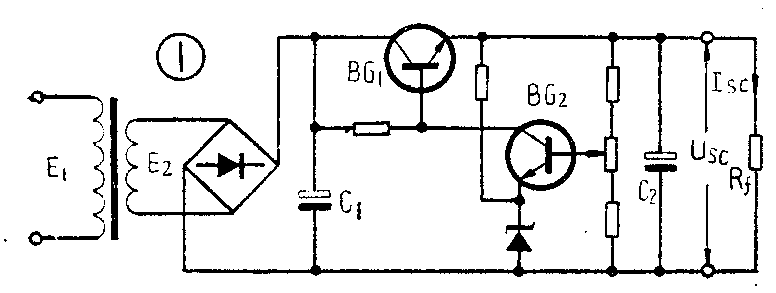
串联型晶体管直流稳压电源应用已十分广泛,它的基本电路如图1所示。在这个电路中,当输出电压U\(_{SC}\)和输出电流ISC确定后,要精确地计算出交流输入电压E\(_{2}\)和滤波电容C1的容量是比较麻烦的。我们在计算过程中,抓住主要矛盾,忽略那些影响较小的参数,就可以使计算简单,并且选取的C\(_{1}\)能保证使用中的精度,而避免由于容量选得太大造成浪费。
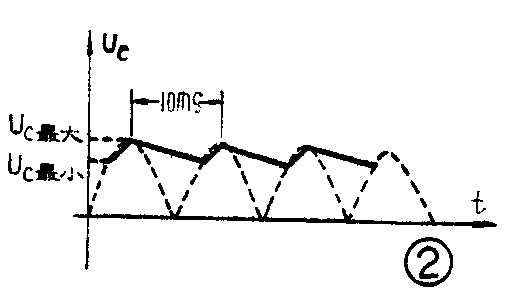
当该稳压电源工作时,滤波电容C\(_{1}\)两端的电压UC是周期性变化,如图2所示。对于50赫的市电电压,这个U\(_{C}\)的变化周期为10毫秒。因变压器次级绕组的内阻和整流桥的内阻都很小,若忽略其电压降,那么C1上的电压U\(_{C}\)将以10毫秒为周期充电到接近次级两端电压峰值\(\sqrt{2}\)E2。由于输出电流I\(_{SC}\)远大于图1电路中的取样电流、稳压二极管电流和调整管BG1的驱动电流之和,所以可视为电容C\(_{1}\)在充电到接近2E2后,是以I\(_{SC}\)值恒流放电的。因而UC在每个充放电周期内是由接近\(\sqrt{2}\)E\(_{2}\)时开始呈线性下降的。它的最长放电时间是10毫秒,由此可知,C1在一个充放电周期内它两端的电压变化量是C,
C=C1=I\(_{SC}\)·t;C1(1)
式中荂\(_{1}\)放电时放出的电量,t是放电时间(此处近似10毫秒)。
C\(_{1}\)充电所能达到的最大电压UC最大=\(\sqrt{2}\)E\(_{2}\)-UD(2),式中U\(_{D}\)是整流桥的压降。此时忽略了次级绕组内阻上的压降。
C\(_{1}\)放电后的最低电压UC最小受输出电压U\(_{SC}\)和调整管BG1的电压U\(_{Ce1}\)的限制,为保证输出电压为额定值,必须使UC最小≥U\(_{SC}\)+UCe1可以认为U\(_{C最小}\)=USC+U\(_{Ce1}\)(3)。
在一个充放电周期内,C\(_{1}\)上的电压变化量C应等于C\(_{1}\)上最大电压和最小电压之差,即C=U\(_{C最大}\)-UC最小,将它代入(1)式,得U\(_{C最大}\)-UC最小=I\(_{SC}\)·t/C1,
C\(_{1}\)=ISC·ι\(\sqrt{2}\)E\(_{2}\)-UD-U\(_{SC}\)-UCe1
从上式中,可以看出C\(_{1}\)的大小不仅与输出电压、电流有关,还与变压器次级电压E2等有关。用这个公式可以很方便地算出所需的C\(_{1}\)值。
例如:设计一个串联型晶体管直流稳压电源,输出电压12伏,最大负荷电流2安,变压器次级绕组电压取18伏,求滤波电容C\(_{1}\)的数值。
我们可以按公式直接计算。一般调整管压降U\(_{Cel}\)取3伏,UD取2伏,那么
C\(_{1}\)=2×10×10\(^{-}\)3\(\sqrt{2}\)×18-12-3-2
=2300(微法)
如果手头已有一只电容,容量为3000微法,则可根据上式,选定变压器次级边的电压E\(_{2}\)。
E\(_{2}\)=1\(\sqrt{2}\)(ISC·t;C\(_{1}\)+USC+U\(_{D}\)+UCe1)=16.7(伏)
这样计算出的C\(_{1}\)或E2都是设计时允许的最小值。若考虑到电网电压的波动,一般可按计算的结果增加10%来选取C\(_{1}\)、E2数值。在计算过程中,我们取C\(_{1}\)的放电时间为10毫秒,实际上小于10毫秒,因此计算出的C1值将比实际偏大。另外,计算时忽略了次级绕组电阻的影响,所以C\(_{1}\)上的实际最大电压要低些,这就使计算的C1值偏低。这两项相互补偿,使计算结果能保证足够的精度。(刘铁城)