随着数字集成电路的迅速发展,用集成电路逻辑门构成的各种脉冲电路已获得日益广泛的应用。本文重点介绍几种用国产TTL与非门(如7MY13、7MF11等)组成的自激多谐振荡器。
图1是7MY13型与非门的内部电路。图2是一种用两个与非门F\(_{1}\) 和F2组成的对称型自激多谐振荡器。下面我们详细分析它的工作原理和元件参数的选择。
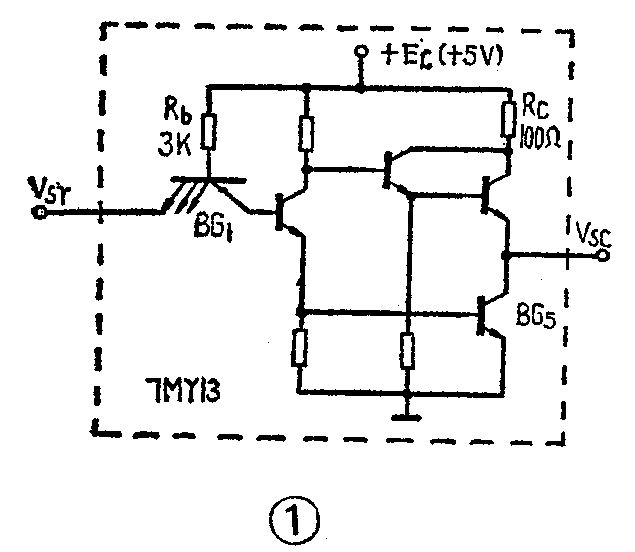
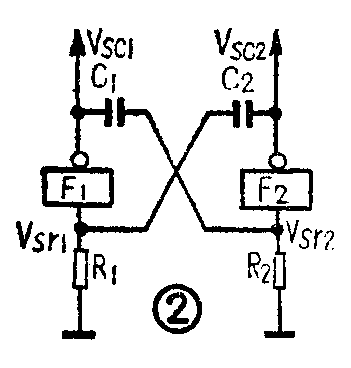
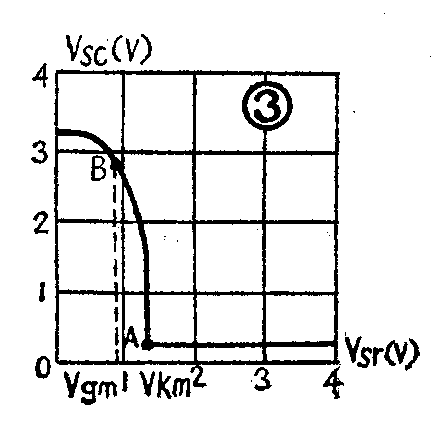
接通电源后,就会有电流分别流过电阻R\(_{1}\)和R2,在它们的上面产生电压降,成为门的输入信号V\(_{sr1}\)和Vsv2。根据图3所示的TTL与非门电压传输特性曲线,适当地选择R\(_{1}\)、R2的阻值,使这个电压降稍大于与非门的关门电平V\(_{gm}\)(约0.8伏),则电路工作在电压传输特性的线性部分BA段,两个门的输出电位Vsc1和V\(_{sc2}\)都要下降。由于两个门电路不可能绝对对称,假定F2门的输出电位下降快一点,它通过电容C\(_{2}\)的动态耦合,作用在F1门的输入端,使V\(_{sr1}\)下降,F1门的输出电位V\(_{sc1}\)就要上升,经过C1的动态耦合,反馈回来使F\(_{2}\)门的输入电位Vsr2上升,于是F\(_{2}\)门的输出电位Vsc2进一步下降……。这就形成了正反馈的连锁反应,量变引起质变,在极短的时间内使F\(_{1}\)门关闭,F2门开启,即V\(_{sc1}\)为高电位Vcg,V\(_{sc2}\)为低电位Vcd,电路进入第一暂稳状态。
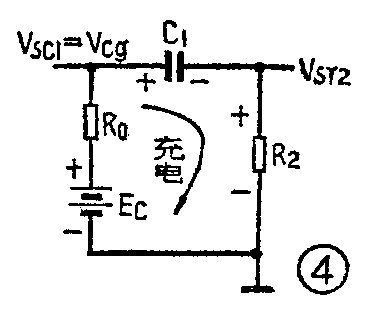
这一状态是不能持久的,因为当V\(_{sc1}\)跳变到高电位后,电容C1就开始充电,充电回路为EC→R\(_{0}\)→C1→R\(_{2}\)→地,如图4所示(R0是与非门输出高电位时的输出电阻,其值约为100Ω)。初始充电电流在R\(_{2}\)上产生一个正跳变,维持F2门的开启,随着充电过程的进行,C\(_{1}\)两端的电压VC1按指数规律上升,则R\(_{2}\)上的电压Vsr2就按指数规律下降(因V\(_{sc1}\)=VC1+V\(_{sr2}\)),当Vsr2下降到小于开门电平V\(_{km}\)时,则Vsc2开始上升,经C\(_{2}\)耦合使Vsr1也上升,则V\(_{sc1}\)下降,又经C1使V\(_{sr2}\)进一步下降,Vsc2进一步上升。这一正反馈的连锁反应,几乎在瞬时,使电路的状态发生突变,导致F\(_{1}\)门由关闭到开启,Vsc1由高电位V\(_{cg}\)跳变到低电位Vcd:F\(_{2}\)门由开启到关闭,Vsc2由低电位V\(_{cd}\)跳变到高电位Vcg,电路进入第二个暂稳状态。
当V\(_{sc2}\)跃变为高电位后,C2将开始充电,充电回路为E\(_{c}\)→R0→G\(_{2}\)→R1→地。随着充电过程的进行,V\(_{sr1}\)按指数规律减小。当Vsr1降低到小于开门电平V\(_{km}\)时,电路中将产生如下正反馈连锁反应
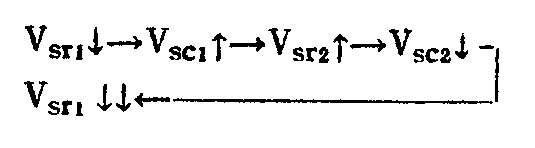
使电路的状态发生突变,回复到F\(_{1}\)门关闭,F2门开启的第一个暂稳状态。然后电容C\(_{1}\)又进入充电过程……如此循环不已,在输出端获得连续的方波。
另一方面,当V\(_{sc2}\)由Vcg跳变到V\(_{cd}\)时,电容C2就要放电,放电回路如图5所示。初始放电电流在R\(_{1}\)上产生一个负跳变,它使F1门更加可靠地关闭。随着电容C\(_{2}\)的放电,放电电流按指数规律减小,Vsr1按指数规律上升,R\(_{1}\)上的电压趋向稳态值IsrR\(_{1}\),只要电阻R1的值不太大,则V\(_{sr1}\)=IsrR\(_{1}\)将小于关门电平Vgm。电容C\(_{2}\)(C1)的放电过程不会影响电路的工作状态,决定电路状态的是电容C\(_{1}\)(C2)的充电。
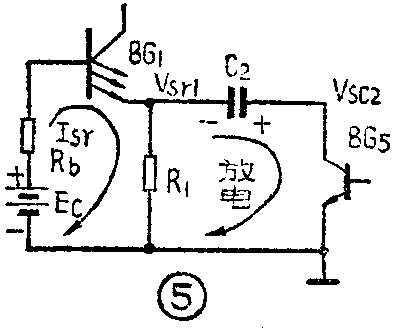
综上所述,由于C\(_{1}\)、C2交替充放电,引起电路状态的不断转换,形成周期性的振荡。电路输入、输出端波形如图6所示。
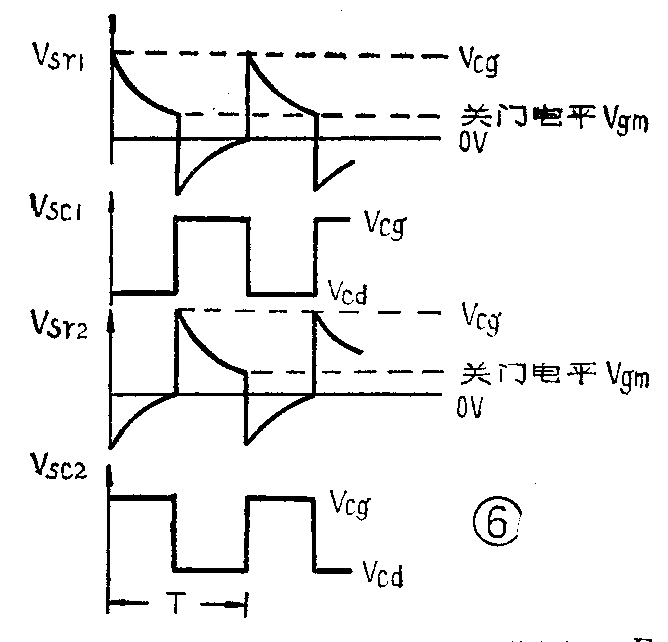
图2的电路中,电容C和电阻R的大小是决定振荡周期T的重要参数,理论推导可得
T≈2.5RC
电阻R的数值太大或太小都不能保证可靠的振荡,一般R的选择范围是
5.5R\(_{C}\)≤R≤4.8Rb
在R值选定后,电容C是决定振荡频率的关键元件,它的数值可根据所需频率的要求由计算及实际调试确定,一般在几十微微法到几十微法范围内选取,从而可以得到几赫到十兆赫的振荡频率。为了使振荡频率稳定,最好选用质量好的瓷介电容器或云母电容器。在频率较低时,建议选用钽电解电容器。必须指出,当频率很高时,与非门本身的平均延迟时间对振荡周期的影响不可忽略,振荡频率高至10兆赫以上时,波形变坏,方波畸变。
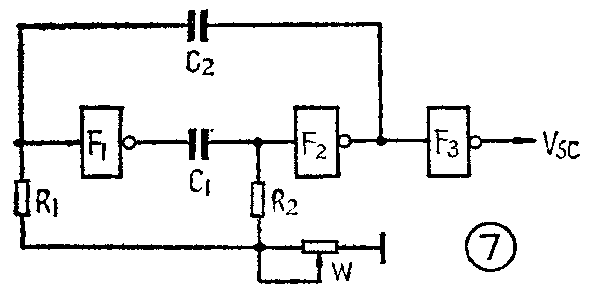
为了使振荡频率能在一定的范围内连续可调,并使输出波形接近于理想方波,可以采用图7的电路,调节W可以在一定范围内改变频率,但W的阻值不可太大,否则不能起振。W一般用1.5KΩ的线缆电位器。F\(_{3}\)门的作用是为了整形。
除了上面讨论的对称型多谐振荡器外,在某些测试仪器中还使用一种环形多谐振荡器,其逻辑原理图如图8所示。它是由三个与非门依次首尾相接组成的环形电路。大家知道,要获得自激振荡,电路不能出现稳定状态。我们先假定图8的V\(_{sc}\)(A点)稳定在低电位,那么经过F1、F\(_{2}\)两级反相后,使C点也稳定在低电位,迫使Vsc变为高电位,这就否定了V\(_{sc}\)能够稳定在低电位的假定。同理,假定Vsc稳定在高电位,则经F\(_{1}\)、F2两级反相后,使C点稳定在高电位,迫使V\(_{sc}\)变为低电位。由此可见,这个电路没有稳定状态,必然会产生自激振荡。
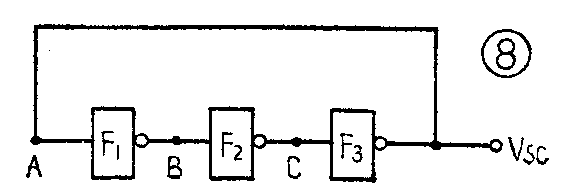
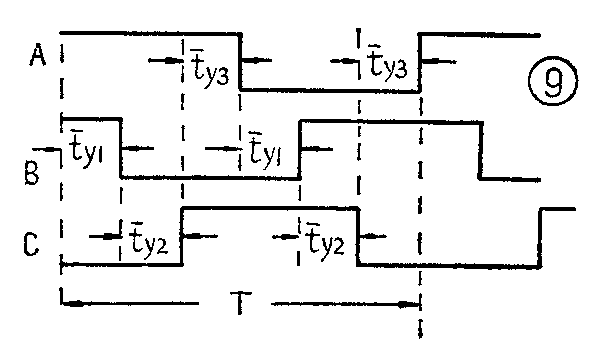
这种简单的环形多谐振荡器的振荡周期完全取决于“与非”门本身的平均延迟时间t-y。我们还是以“1”代表高电位,以“0”代表低电位,设起始状态为A=1,当A达到1的瞬间,经过F\(_{1}\)门的延迟时间t-y1,B才变为0,再经过F\(_{2}\)门的延迟时间t-y2,使C变为1,最后经过F\(_{s}\)门的延迟时间t-y3迫使A变为0。从A=1到A=0,总共需要经历t-y\(_{1}\)+t-y2+t-y\(_{3}\)=T1的时间延迟。同理,再使A=0变为A=1,也需经历t-y\(_{3}\)+t-y2+t-y\(_{3}\)=T2的时间延迟。因此振荡周期为
T=T\(_{1}\)+T2=6t-\(_{y}\)
三级门环形多谐振荡器的原理波形如图9所示。这种多谐振荡器在工作时,由于每一个与非门的平均延迟时间极短(如7MY13约为20~40ns),所以振荡频率很高(用3个门时,f≈10MHz),而且不能调节。另一方面,实际输出波形的前后沿都不陡,不适宜做脉冲信号源,仅应用于集成门电路交流参数测量电路中。
为了获得波形较好频率较低的振荡,可以在电路中接入R、C定时元件。图10就是一种实用的环形振荡器的逻辑电路。在这种电路中,振荡器的定时主要地取决于电容C的充放电速度,不但起振可靠,同时频率可以在很大范围内改变。下面简单分析该电路的工作过程。
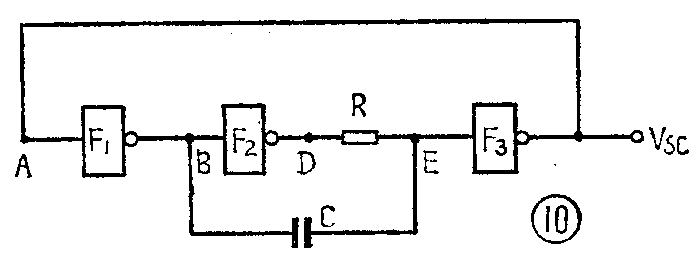
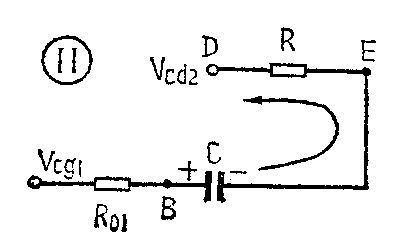
当A点由高电位跳变到低电位时,B点由低电位跳变到高电位,它一方面经F\(_{2}\)门使D点电位由高变低,另一方面经电容C的耦合,使E点电位也由低变高,使F3门开启,使A点处于低电位,这就是第一暂稳状态。
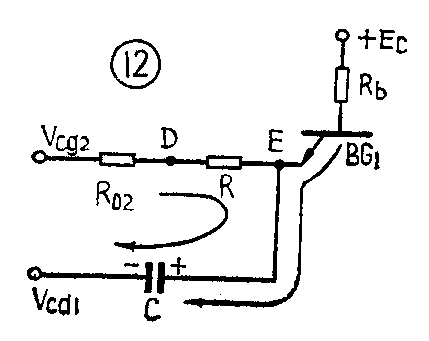
电路状态的变化,引起电容C的充电,充电回路如图11所示。充电电流在电阻R上的电压降维持F\(_{3}\)门开启。随着充电过程的进行,充电电流按指数规律减小,E点电位按指数规律下降,当E点电位降低到关门电平Vgm时,F\(_{3}\)门关闭,A点电位由低变高,B点由高变低,D点由低变高,E点下跳到较负的电压值,确保F3门关闭,电路进入第二个暂稳状态。这时,由于D点处于高电位,B点处于低电位,所以电容C被反方向充电,其充电回路如图12。随着充电过程的进行,E点电位按指数规律上升,L升到开门电平V\(_{km}\)时,电路就从第二暂稳状态迅速跳变到第一暂稳状态。如此循环不已,在电路的输出端就获得连续的方波。这种电路的振荡周期为
电阻R的阻值不能太大,一般取几百欧姆,否则可能停振,电容C根据所需频率可在几十微微法到几百微法的大范围内选取。
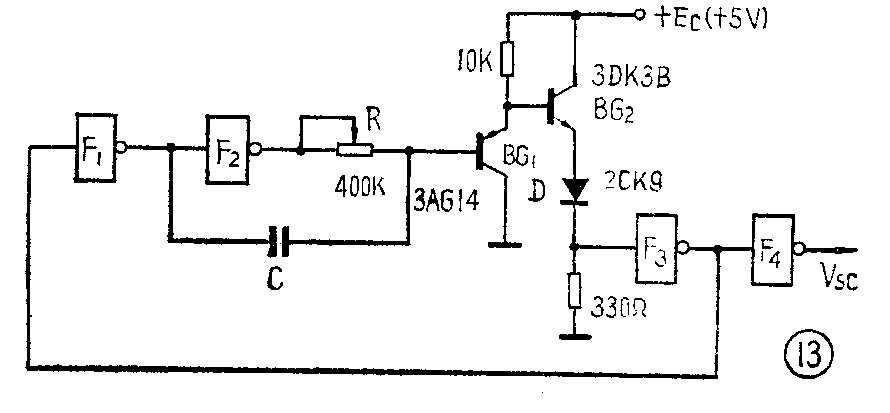
为了使环形多谐振荡器的振荡频率在小范围内连续调节,可以用电位器W代替电阻R。图13是一个实际的频率可调的环形振荡器,电路中增加了由BG\(_{1}\)、BG2组成的两级射极跟随器,由于它的输入电阻很高,所以隔离了F\(_{8}\)门对RC定时电路的影响,并且R可以选用阻值很大的电位器,以获得较低频率的振荡,又由于它的输出电阻很小,使输出方波的上升沿较好。F4门是一个反相器,作整形用。(宋东生)