前面讲过,由四级双稳态电路组成的十进制计数单元,具有十个稳定状态,可以用十个四位二进制数码来表示,它们分别代表0、1、2、……9十个数字。这种用二进制数码表示十进制数的方法,称为“二—十进制编码”。我们已经介绍了几种常用的编码方案,譬如在“8、4、2、1”代码十进制计数单元中,十进制数的0用代码“0000”表示,十进制数的9用代码“1001”表示;而在余3代码十进制计数单元中,十进制数的0用代码“0011”表示,十进制数的9用代码“1100”表示等等。
在数字设备中,为了把计数单元的十个计数状态以十进制数的形式通过显示器件清楚而直观地显示出来,就需要在计数单元与显示器之间接入“译码器”。
译码器就是把代码“翻译”成编码原意的电路。以打电话作例子来说,成千上万台电话机,每一台都预先编上号码,当你拿起送受话器拨“117”时,电话只能通到报时台,而不会通到其他单位。你只是拨了几个数字,但机器却自动地从成千上万条电话通道中找出你所要的那一路,也就是把代码“翻译”成编码时确定的原意。在十进制计数单元中,十进制数字的显示器件中十个数字的点亮与熄灭,分别通过十个晶体管开关进行控制。当某一个晶体管开关的基极输入为高电平时(以NPN型晶体管为例),该晶体管饱和,相当于开关接通,与之相应的数字点亮,其余九个晶体管开关的基极输入都是低电平,使这些管子截止,所以这九个数字不亮。为了使显示器显示的数字确切地反映出十进制计数单元的相应的计数状态,就需要把计数单元的十个状态变为驱动显示器十个晶体管开关“接通”或“断开”的控制信号,这一过程是由“译码器”来完成的。和上面所举的“打电话”的例子相仿,只要十进制计数单元给出了某一二进制数码,译码电路就能自动接通与它对应的某一个数字的显示开关,使该数字点亮。为此,对译码器的基本要求是:(1)把计数单元中的各人代码以电平高低的形式在十根输出线上给出(或称译出);(2)每一个代码只能使一根输出线输出高电平,其余九条输出线全部输出低电平。由此可见,译码器实质上是一种“条件开关”,十条输出线中哪一条输出为高电平是由计数单元的计数状态决定的,也就是说它是有条件的。大家所熟悉的门电路就是一种条件开关。
我们知道,与非门的输出再经一级与非门作反相器,则就变成与门,适合“输入全高,输出为高;输入有低,输出为低”的规律,这种规律,恰好适用于译码电路,以实现对输入代码的翻译。
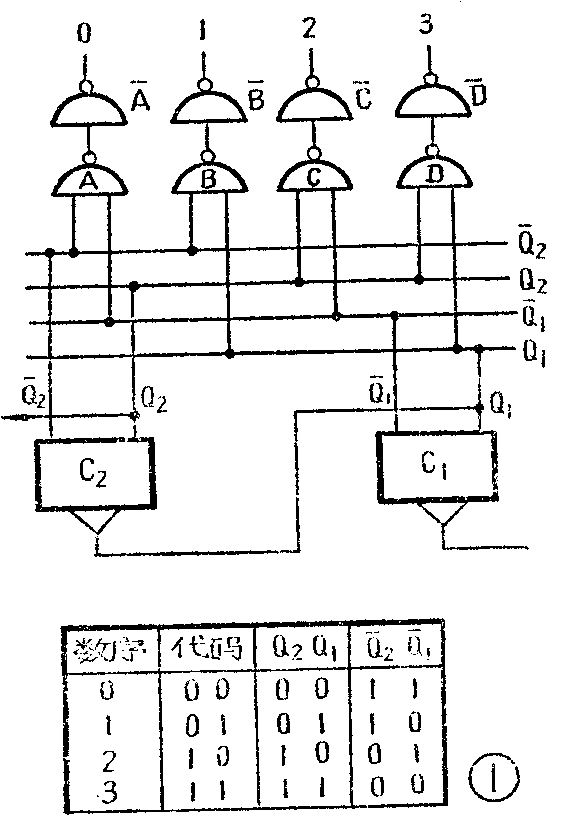
以二级双稳态电路组成的二进制计数器为例(图1),二级双稳共有四条输出线:Q\(_{1}\)、Q-1、Q\(_{2}\)、Q-2,可以组成四种状态:00、01、10、11,分别表示十进制数:0、1、2、3。我们可以用计数器的四条输出线分别控制四组与非门,每组与非门分别用来判别并取出四个代码中的一个。如果输入代码是00(表示数序0),这时,Q\(_{2}\)和Q1都是“0”,Q-\(_{2}\)和Q-1都是“1”,第一个与非门A的输入就引自高电平端Q-\(_{2}\)、Q-1;如果输入代码是01(表示数序1),这时Q\(_{2}\)=“0”“Q1=“1”,而Q-\(_{2}\)=“1”、Q-1=“0”,第二个与非门B的输入引自这时的高电平端Q\(_{2}\)、Q1;同理,表示数序2的代码是10,第三个与非门C的输入引自这种状态时的高电平端Q\(_{2}\)、Q1;第四个与非门D的输入引自Q\(_{2}\)、Q1,当00状态到来时,0号线出现高电平,而其他三个与非门B、C、D均因“输入有0”而处于“输出为1”的状态,再经与非门反相后为“0”,故1、2、3号线没有信号输出,这就把0号线所对应的状态从中取出来了。同理,当计数器处于01状态时,只有1号线是高电平;处于10状态时,只有2号线是高电平;处于11状态时,只有3号线是高电平。四个代码就是这样通过与非门译码器“翻译”出来的。
为了便于认识译码器所遵循的规律,以8·4·2·1代码二—十进制计数器为例,将8·4·2·1代码二—十进制的“数”与电路的“状态”之间的关系列于表1。由表1可见,不论哪一个“数”,计数器总有四个输出端为“0”、四个输出端为“1”。
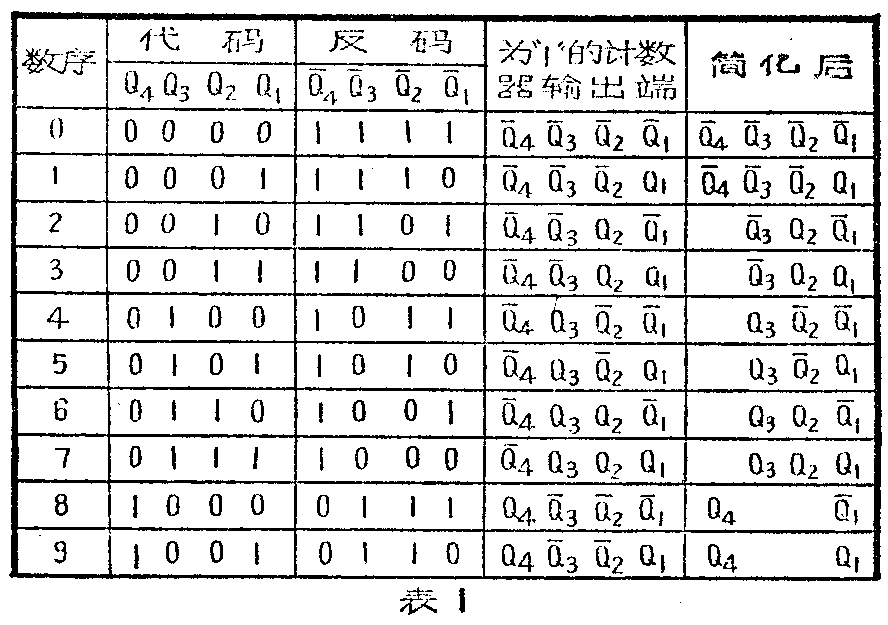
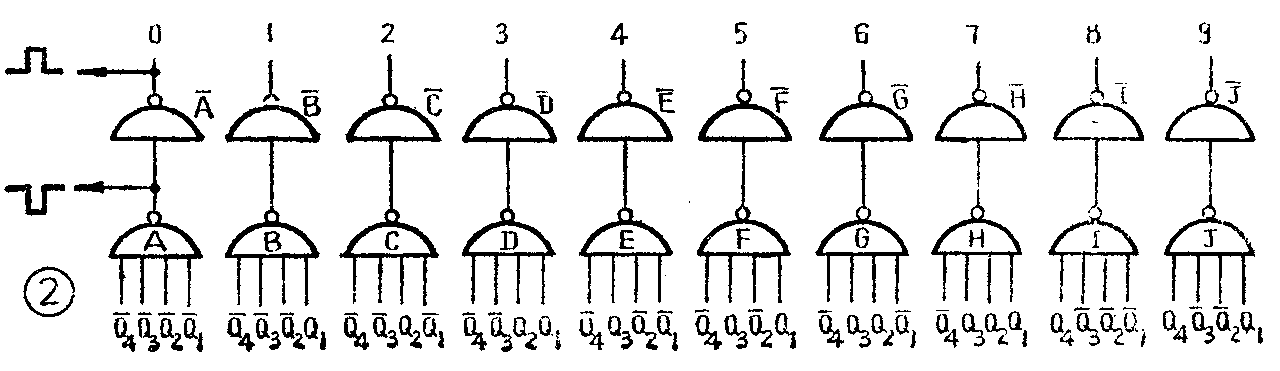
如果象图2所示那样,用十组与非门电路,将A至J的十个与非门的输入端分别和表2中每个“数”相应的四个高电平端相连,例如译出十进位数0的与非门和Q-\(_{4}\)、Q-3、Q-\(_{2}\)、Q-1相连,译出十进位数1的与非门和Q-\(_{4}\)、Q-3、Q-\(_{2}\)、Q-1相连,……,当相应的电路状态出现时,与之对应的门电路就开门,其它的门电路都关门。如在图2中,当Q-\(_{4}\)、Q-3、Q-\(_{2}\)、Q-1均为“1”时,与非门A输出为“0”,与非门A输出为“1”,其余与非门从B-至J-的输出端都是“0”状态。这样就使“0000”状态从其它各种状态中分离出来。若将Q-\(_{4}\)、Q3、Q\(_{2}\)、Q1连到与非门H的输入端,则当十进位数7的状态“0111”到来时,因H输出为“0”,H-输出呈高最平“1”,其它均为低电平“0”,余类推。由于在某一时刻,只能出现一种状态,所以同一时刻只有一条输出线是“1”状态,表示某个确定的“数”。
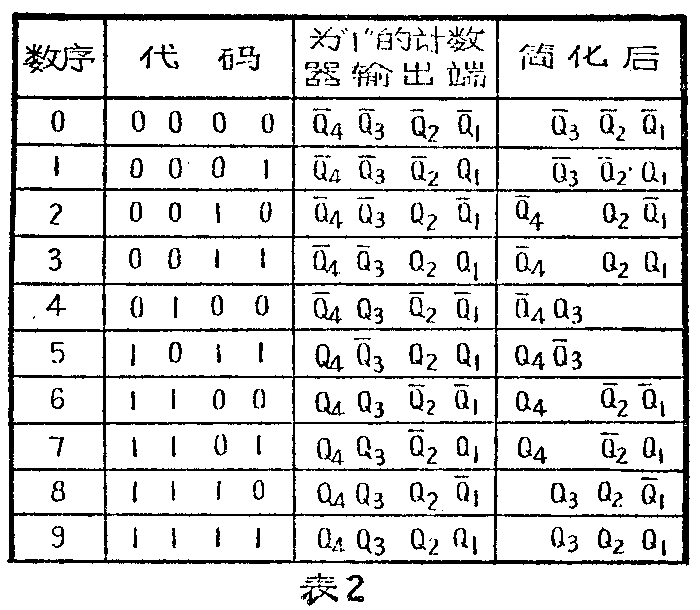
如果省略与非门A--……J-,而直接从与非门A、B、C……取出信号,则取出的是负向信号,即当某个状态如7到来时,只有门H的输出为低电平“0”,而其余与非门的输出均为高电平“1”。
对不同的编码制,译码电路各输入端与计数器输出端的连接程序也将随之而异。例如互补2·4·2·1代码与不同数序对应的计数器高电平输出端加表2所示,所以用互补2·4·2·1代码时,译码器每个与非门的输人端,要换成与表2中所列相适应。对于余3代码,换成表3所示的情况。
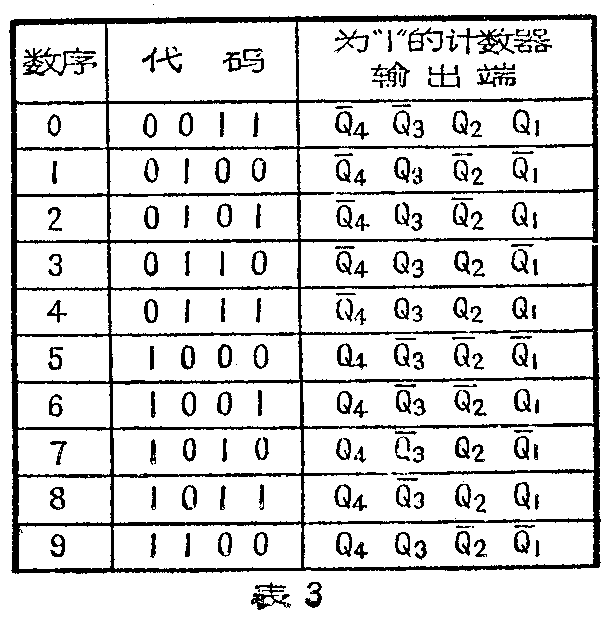
图2所示的译码器,每个与非门都得有四根输入线,而且如Q-\(_{4}\)端,在8·4·2·1代码中要接到八个门电路的输入端,负载较重。能不能简化译码器中每一个数字的鉴别方法,减少一些连线呢?
让我们来分析一下8·4·2·1代码的特点,举“9”这个二—十进制码“1001”为例,实际上只要根据Q\(_{4}\)和Q1这两位是“1”,就可以判定这个8·4.2·1码必定是“9”。因为Q4-=1,在8·4·2·1码中只有“8”和“9”这两个可能,若再加上Q1-=1,就完全确定这个数不是“8”,而只能是“9”了。这说明了图2中与非门J的二个输入端Q-\(_{3}\)和Q-2是可以省去的。
同样道理,“8”这个码“1000”也只要根据Q\(_{4}\)、Q1是不是“1、0”来判断,这样就可以减少两根连线。再分析其它数字,可以看出,“2”到“7”(即从“0010”到“0111”)这六个数字都可以根据8·4·2·1码的后三位来进行判断,省去Q-\(_{4}\)这根连线并没有影响。
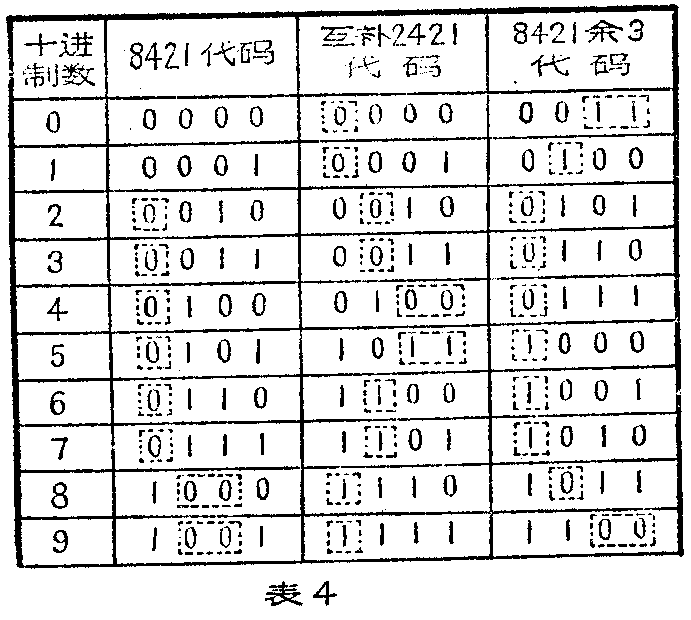
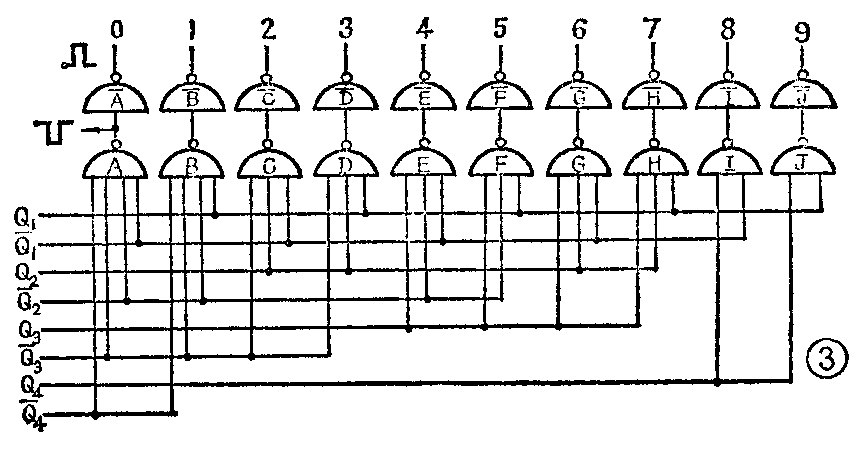
对其它各种代码,也可以进行简化,如表4所示,虚线方框中的数码所对应的连线可以省去不用。图3是简化后的8·4·2·1代码的译码器。
如何把译码器得到的结果很直观地用十进制数字显示出来,使操作人员直接读取数据呢?这个任务由显示器来完成。显示器就是能直接显示十进制数字0、1、2、……9的电子器件。目前最常用的显示器有辉光数字管和荧光数码管,有些数字设备则采用边光显示器和投影显示器。随着数字集成电路的迅速发展和应用,从事显示技术的广大工人和科技人员又研制出许多新颖的显示器件,如场效应发光元件、电子束显示管、等离子数字显示器以及液晶显示器等,为数字设备的微小型化、低功耗和高可靠性展示了广阔的前景。本文只介绍使用极为普遍的辉光数字管显示器。
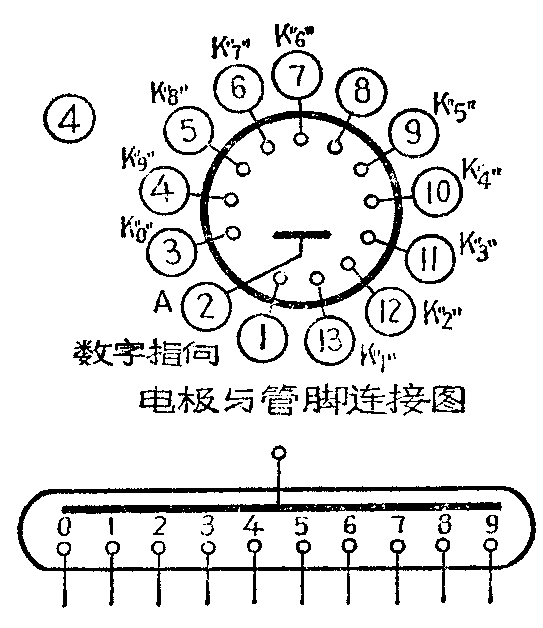
辉光数字管是利用辉光放电的原理制成的。在充有氖气的玻璃管内,装有一个公共的阳极和十个阴极,这十个阴极分别用金属丝做成0、1、2、……9等十个数字的形状,在管芯内用陶瓷绝缘子把它们相互分隔叠装在一起,十个阴极和阳极分别引线焊接在对应的管脚上,图4是它的管脚和符号图。辉光数字管有端面显示和侧面显示两种,图5是它的工作原理图,当某个阴极为低电平并与阳极形成回路,这个阴极的数字就点亮。
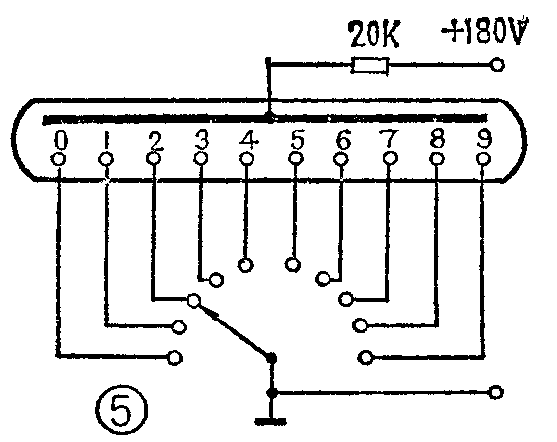
由于辉光数字管需要高电压产生强电场才能起辉,起辉电压大于150伏,所以阳极直流供给电压取180伏。阳极电流2毫安。从与非门输出到辉光数字管之间,必须加能耐高压的晶体管组成驱动电路,驱动电路一般都用高反压晶体管,如3DG405~409,也可以用可控硅。在阳极电路里,还需要串接一只电阻,起限流作用。
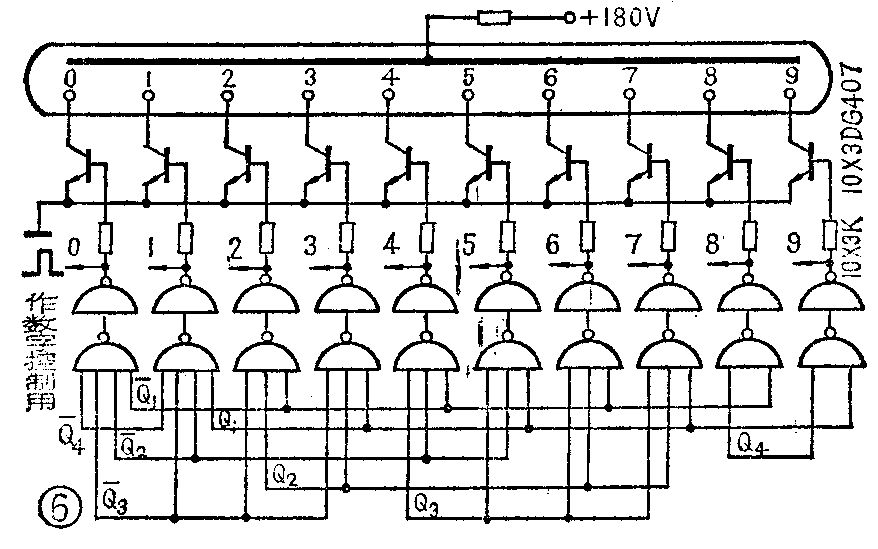
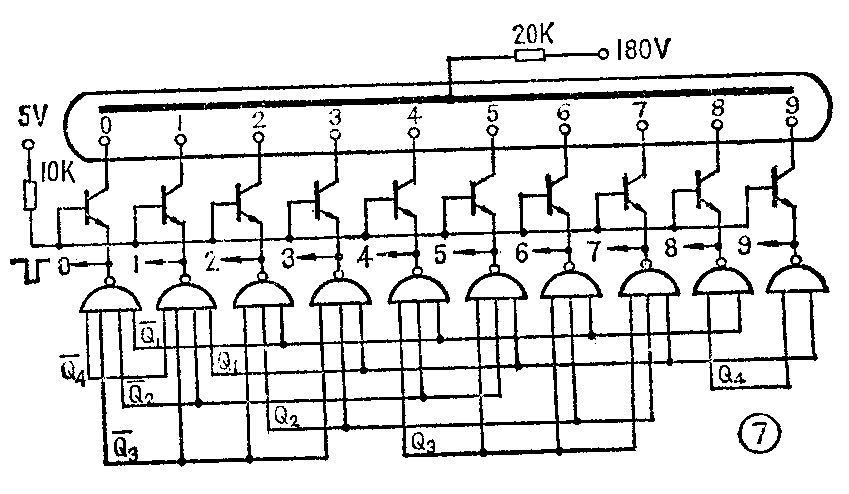
图6和图7把译码器和显示驱动器画在一起。图6将十个与非门(反相器)输出经3千欧电阻分别连到驱动晶体管的基极,十个晶体管的发射极连在一起接地,当某个译码与非门的输入端全部为“1”电平时,该译码与非门输出为“0”电平,再经反相,使输出为高电平,相应的晶体管导通,数字管中相应的阴极数字点亮。其他各反相门的输出均为低电平。图7中将十个译码与非门的输出直接接到驱动晶体管的发射极,十个晶体管的基极连在一起串联10千欧电阻接到5伏电源,当某个译码与非门输出为低电平时(不必再经过反相),相应的晶体管导通,数字管中相应的阴极数字点亮。
当我们了解了显示驱动电路以后,再回过来分析一下图6及图7所示的译码电路,我们可以发现,这样的译码电路还可以简化。从8·4·2·1代码简化后的译码表(表1)可以看到:(1)凡是偶数都有Q-\(_{1}\),凡是奇数都有Q1,(2)相邻两数如“0、1”,“2、3”,……等,除了Q\(_{1}\)、Q-1的差别外,其它输入端都相同。例如0与1都有Q-\(_{4}\)Q-3Q-\(_{2}\);而2与3都有Q-3Q\(_{2}\)等等。因此,可以把公共输入端Q-4Q-\(_{3}\)Q-2或Q-\(_{3}\)Q2等都加到0、1或2、3显示驱动晶体管的基极作为0或1、2或3点亮的必要条件,但究竟相邻奇数偶数中哪一个接通,还要取决于Q\(_{1}\)和Q-1。因此,可以把相邻二个数字(如0和1)的显示简化成图8所示那样。
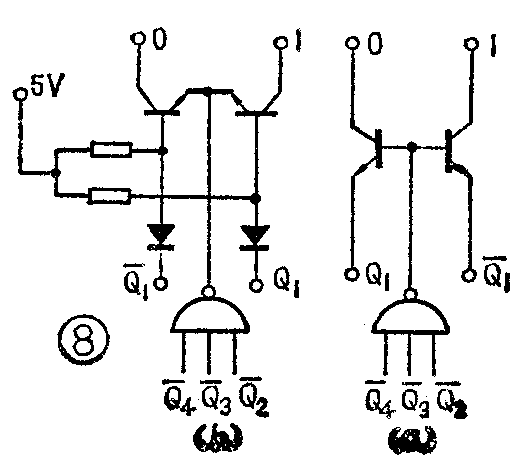
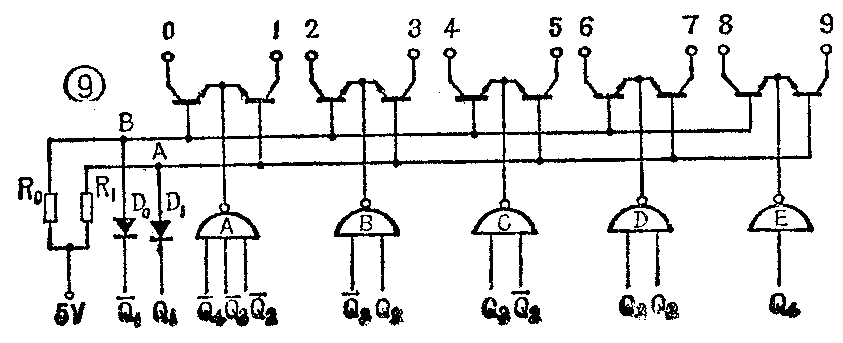
图9是经过这种简化后的8.4.2.1代码二—十进制计数器的译码和显示驱动电路。图中奇数和偶数晶体管的基极分别连在一起,各自接到Q-\(_{1}\)和Q-1。我们知道,对于NPN型晶体管来说,当基极电位小于发射极电位时,必定处于截止状态。而Q\(_{1}\)和Q-1两端,当一端处于高电平时,另一端必定处于低电平。因此,在同一时刻,只需鉴别五个状态。当状态为“0000”时,Q\(_{1}\)=“0”、Q-1=“1”,二极管D\(_{1}\)导通,A点电位被箝制在D1的正向压降0.7伏低电位上,故奇数晶体管处于截止状态,而B点电位为高电位,偶数晶体管有可能导通。因为当状态为“0000”时,Q\(_{4}\)、Q3、Q\(_{2}\)为“1”电平,五个与非门中只有与非门A输出为低电平,所以只有0号晶体管具有导通的充分条件,而其它九个晶体管都截止。当状态为“0001”时,Q1=“1”、Q-\(_{1}\)=“0”,D0二极管导通,B点为低电位,偶数晶体管截止。A点为高电位,奇数晶体管有可能导通。当Q-\(_{4}\)、Q-3、Q-\(_{2}\)为“1”时,与非门A输出仍为低电平,但这时只有1号晶体管导通,其它晶体管均截止。其余各个状态的译码,以此类推。
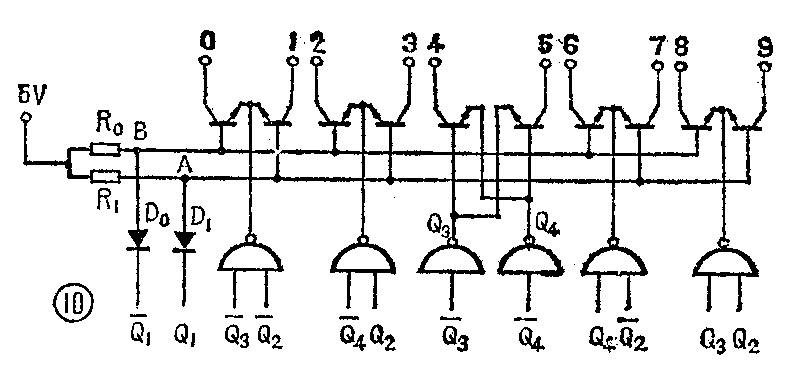
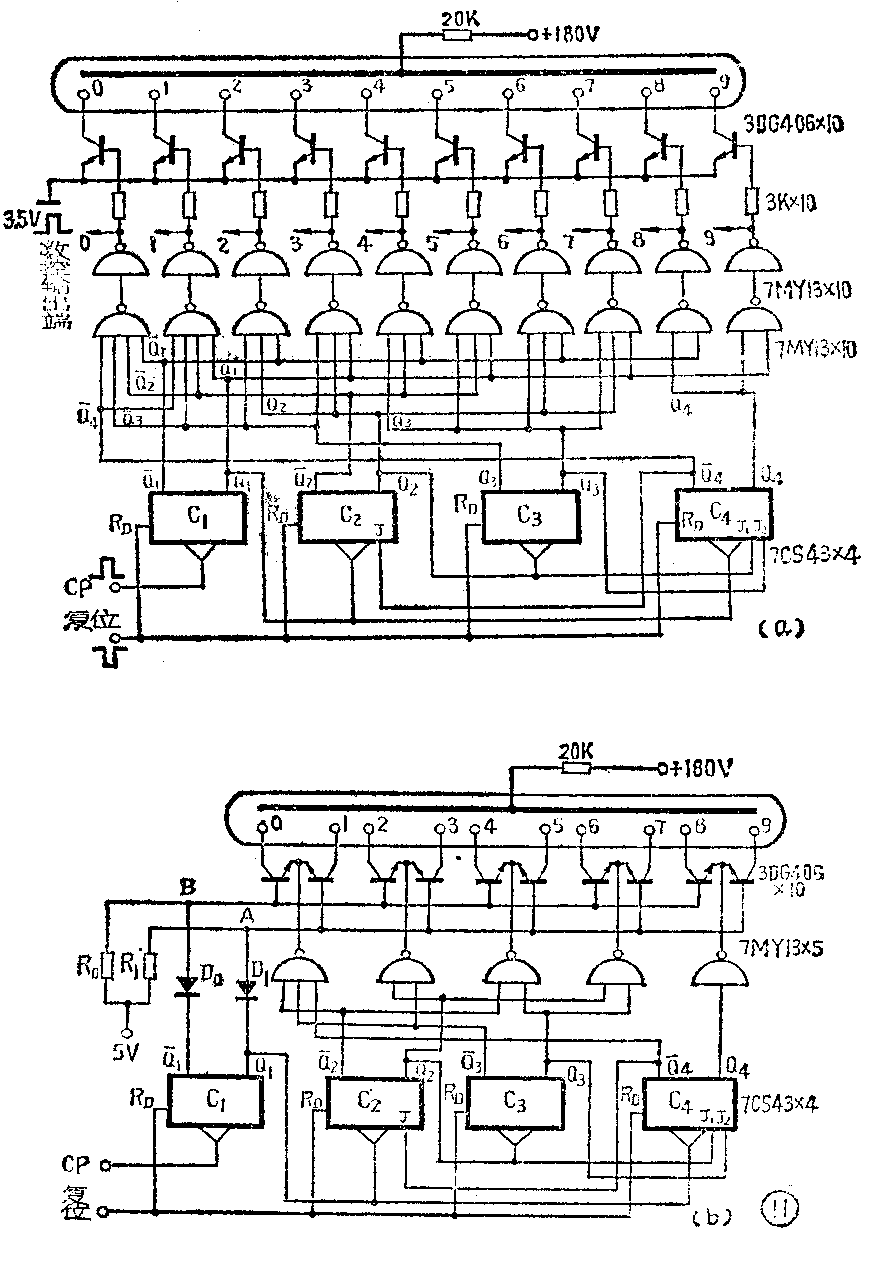
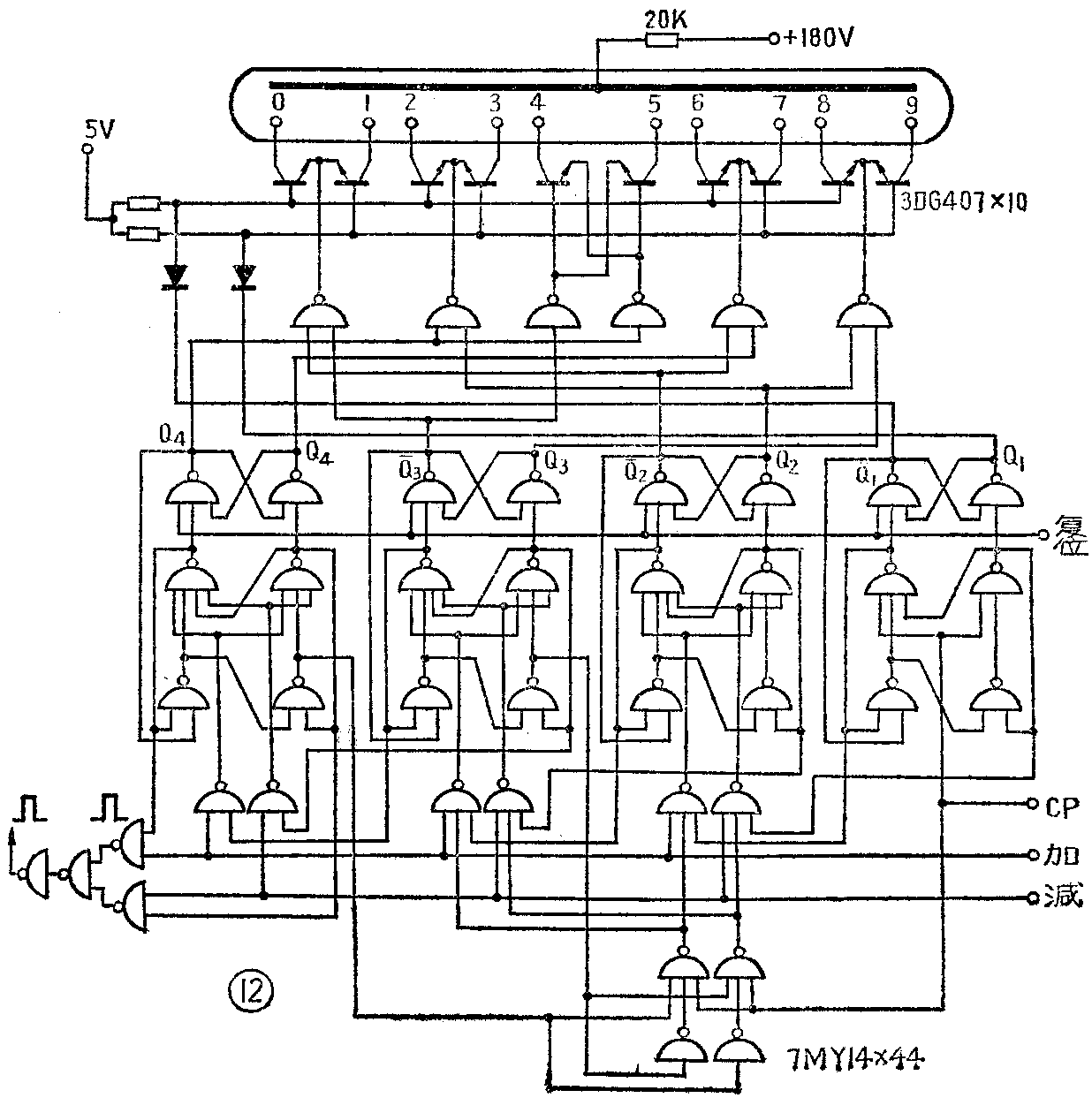
图10是互补2.4.2.1代码奇偶译码电路,此电路可以对照表2来分析。其中Q\(_{1}\)、Q-1和图9相似,Q\(_{1}\)端接到奇数晶体管的基极,Q1端接到偶数晶体管的基极,所不同的是4和5这一对晶体管是分开的,这是由互补2.4.2.1代码的特点决定的。当Q\(_{4}\)和Q3呈“01”状态时,晶体管4的发射极为低电平而基极为高电平,晶体管4导通,其余九管均截止。当Q\(_{4}\)、Q3呈“10”状态时,晶体管5的基极为高电位,发射极为低电位,管5导通,其余九管均截止。图11是二种由JK触发器组成的8·4·2·1代码二—十进制计数器的计数、译码、显示电路,从图可看到单位计数器的全貌。图12是一种由维持阻塞触发器组成的互补2·4·2·1代码二—十进制可逆计数器的计数、译码、显示电路,是单位可逆计数器电路的全貌。(天津市四十二中学 凌肇元)