集成电路计数器

在毛主席关于“教育要革命”的伟大指示指引下，我校办起了校办工厂，使它成为教学、生产、科研三结合的基地。在校办工厂中，教师和同学一起参加劳动，参加试制，向工人师傅学习，向生产实际学习，既锻炼了思想，又增长了才干。

在校办工厂中，我们学集成电路，用集成电路，并且将集成电路做成计数器，批量生产数字计时器，计数插件板等数字仪表，在教育为无产阶级政治服务，为工农兵服务，与生产劳动相结合方面，取得了可喜的成果。

本文是根据我们的实践经验整理出来的，力图从理论和实际的结合上讲明集成电路计数器的基本原理以及在实际运用中遇到和解决的具体问题。

生产实践中变化着的各种物理量，可以通过光电、声电、热电、压电、磁电等效应，转换成电脉冲信号，输入计数器。计数器则通过电路元件本身固有的特殊功能，组成不同的电路状态来表示不同的“数”，将输入的脉冲信号，按“数”的关系，一、一接收下来，进行传送、运算，并且通过数字管显示出来。所以，计数器的基本思想就是把电路不同的稳定状态跟“数”对应起来，用状态的有规律的变化表示“数”的规律性变化。

一提起数，我们就会想到日常生活中习惯使用的十进位计数制，一般数字仪表、小型程控装置、台式计算机和数控计数器的数字管都按十进制显示。但是，在电子技术中很难找到这样一种基本单元电路，它具有十个不同的状态，用来代表十个数。而有两个不同稳定状态的电路，则很容易找到，如双稳态触发器就具有二个稳定的状态。其实，具有两个不同状态的事物的相互转化是极为普遍的，如电灯的亮和暗，电路的通和断，脉冲的有和无，晶体管的导通和截止等等，这反映了普遍的对立统一规律。因此，通常就将十进制的数“编”成数字装置容易接受的二进制的数，经数字装置运算后，再把二进制的数“翻译”成人们所习惯的十进制。在数字技术中，用符号“0”和“1”表示上述两种对立的状态，譬如，把输出低电位记为“0”，输出高电位记为“1”。我们把它们叫做“代码”。显然，代码只是一种符号，它们不同于十进制数字运算中的0、1、2、3…。

电路的不同状态跟数是怎样的对应关系呢？也就是说用怎样的代码组合来表示一个个的数呢？这项工作，叫做“编码”，编码的方案可以有很多种。

把计数电路所算出的二进制结果，“翻译”成十进制数，叫做“译码”，由门电路构成的“译码器”肩负着这项任务。

译码以后的十进制数，再通过显示电路和数字管显示出来。

所以，一般说来，计数器包括按一定编码要求的计数电路，把二进制结果译成十进制的译码器和把十进制数表示出来的显示器这三个基本部分。

我们从计数电路的基本单元双稳态触发器着手分析。双稳态触发器的原理在“无线电”74年第5期中已作过介绍，这里仅就它作为计数触发器单元，概括一下它的特点：

（1）双稳态触发器有两个输出端Q和Q-（见图1），这两个输出端的电位高低总是相反的。因为双稳态电路一管的截止促使另一管饱和，而一管的炮和又保证了另一管的截止。二者既对立，又互相依存，共同存在于触发器这个统一体中。这种状态是有条件的、相对的、可变动的。在外界触发信号作用下，互换成另一种状态。利用它的这种特性，双稳态触发器可作为计数电路中的“记忆”元件。

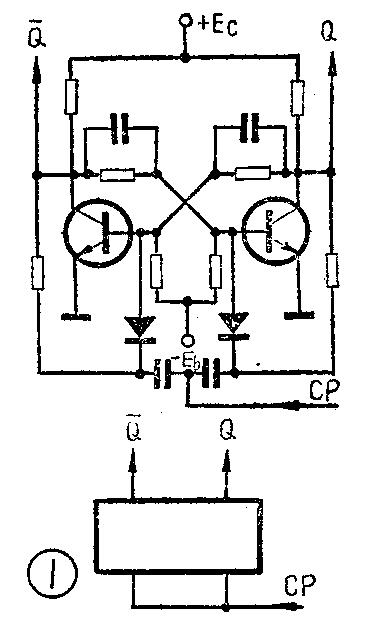
（2）Q为“1”、Q-为“0”的状态，和Q为“0”、Q-为“1”的状态，都是相对稳定状态，所以叫双稳态。整个双稳态触发器的状态。规定以右边输出端Q为准，Q端为“1”，称触发器的状态为“1”；Q为“0”，称触发器的状态为“0”（见图2）。

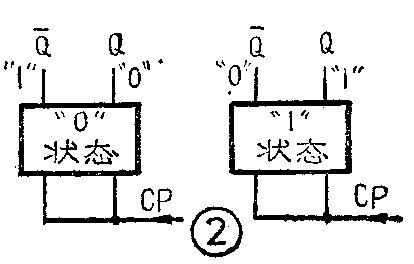
（3）从CP端每输入一个触发脉冲信号，两个输出端Q和Q-就互换一下状态，叫触发翻转（触发器的初步概念即由此而来）。每输入两个脉冲，Q和Q-都回复到原先的状态，但经历了一次变换，即输出一个脉冲信号，这个信号，叫进位信号。所以，双稳态触发器每输入二个触发信号，就输出一个脉冲信号，即进一位（见图3）。从物理意义上来说，对输入信号作了二分频，因而双稳态电路可作“二分频（÷2）电路”。

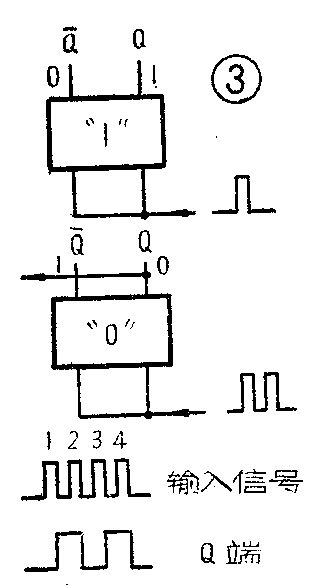
（4）双稳态触发器，服从“逢二进一”的二进制规律。就是说每遇到本位是1，又要加1时，便使本位变0，同时向前面进位，使前一位加1，即1＋1=10。为了说明进位问题，我们将两级双稳态触发器连接起来，如图4。没有输入脉冲信号前的状态为“00”；输入一个脉冲后，第一级双稳态触发器C\(_{1}\)翻转，电路状态为“01”；第二个脉冲输入后，C1翻回为“0”态，并向第二级触发器C\(_{2}\)进位，电路状态为“10”；第三个脉冲输入后，C1又翻转为“1”，电路状态为“11”。如果再输入第四个脉冲，C\(_{1}\)又翻为“0”，并向C2进位，使C\(_{2}\)也翻转为“0”，电路回复到原先的“0 0”，但C2的输出端Q\(_{2}\)向更高位输出一个脉冲。可见，两级双稳态触发器构成的电路，有四个稳态“0 0”、“01”、“10”、“11”，能表示0、1、2、3四个数。这就是双稳态触发器构成计数电路的基本原理。

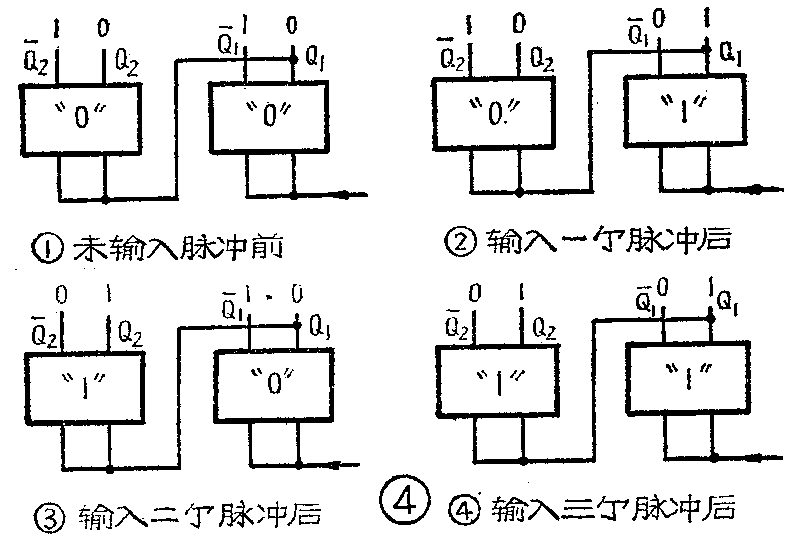
（5）如果采用负脉冲信号触发，那就是指在每当触发脉冲由“1”变“0”（下降沿）时，双稳态触发器才翻转，所以当Q端由“1”变“0”时，才输出给下一级进位信号，而当Q端处于由“0”变“1”的上升沿时，只是作准备，而不输出信号。需用正脉冲信号触发的双稳态触发器，其情况正与此相反。

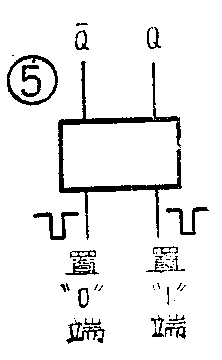
（6）使双稳态触发器的状态变为“0”的输入端，叫置“0”输入端（图5），使双稳态触发器的状态变为“1”的输入端，叫置“1”输入端。从图中看出，Q输出端那一边是置“1”输入端，Q-输出端那一边是置“0”输入端。

从上述双稳态触发器的基本特性知道，两级双稳态能记忆和反映4个数，如果我们要记录更多的脉冲数，就可以把多个双稳态电路逐级连起来。每级取稳态为一个码，级数越多，码的位数越多，通过编码可记录的数也越多，如三级双稳态，有三个码，有2\(^{3}\)=8个不同的状态；四级双稳态，有四个码，有24=16个不同的状态。

输入脉冲的个数和四级双稳态电路的状态两者之间的关系，如表1中左边二列所示，它反映了十进制数和二进制数之间的对应关系。按表1左边二列所示的方式来计数，就是二进制计数法。

用二进制代码表示十进制数的方法，通常称为“二—十进制”代码。从表1可以看出，一位十进制数表1要用四位二进制数来表示，或者说，一只十进位数字管上的0～9十个数（指十进制计数器中的一位），必须由四级双稳态触发器组成。但四位二进制数可代表十六种状态，用来表示十种状态时还需要去掉六种状态，去掉哪六种状态？以及哪一种状态代表十进位的哪个数？这由编码方案来决定。

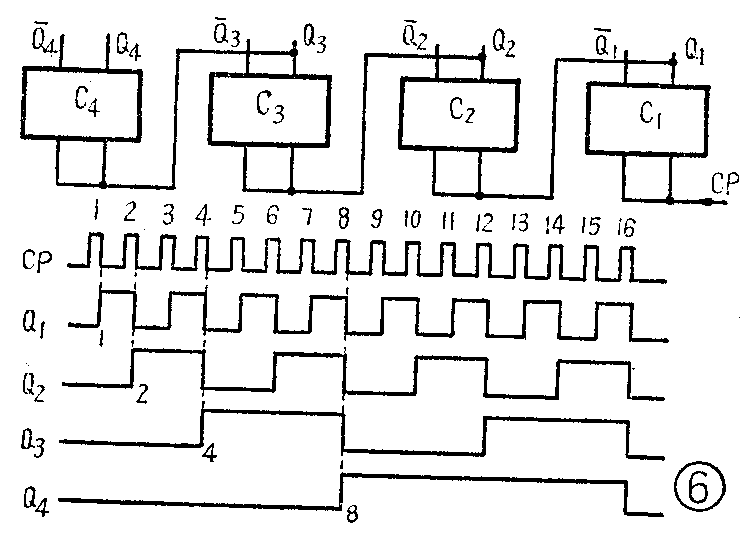
“8、4、2、1”代码是最常用的一种编码方案，它用十六个状态中的前十个状态来代表十进制里的十个数，舍去后面的六个状态（见表1右边的一列）。8、4、2、1是什么意思呢？让我们结合实际回答这个问题，观察一下图6，图中表示的是四级双稳态各级输出波形图，从图中看出，第一级双稳态触发器的第一次翻转（由“0”→“1”）是在第1个输入脉冲的下降沿，第二级双稳态的第一次翻转是在第2个输入脉冲的下降沿，第三级双稳态的第一次翻转是在第4个输入脉冲的下降沿，第四级双稳态的第一次翻转是在第8个输入脉冲的下降沿。结合表1来看，二进制第一位（C\(_{1}\)）为1（“0001”），表示十进制数为1，二进制第二位（C2）为1（“0010”），表示十进制数为2，二进制第三位（C\(_{3}\)）为1（“0100”），表示十进制数为4，二进制第四位（C4）为1（“1000”），表示十进制数为8。取表1中前十个数表示十进制的0—9，这样的编码方案，叫“8、4、2、1”代码（此外还有“2、4、2、1”码等多种）。可见，8、4、2、1是指这种编码的各位所代表的具体数值。“8”就是第四位触发器在十进制数8时开始翻转；“4”就是第三位触发器在十进制数4时开始翻转；“2”就是第二位触发器在十进制数2时开始翻转；“1”就是第一位触发器在十进制数1时开始翻转。因此，根据代码，可以立即得出十进制数与二进制数间的关系。譬如“0111”这个数码相当于十进制数的0＋4＋2＋1=7。又如“1001”这个数码，相当于十进制数的8＋0＋0＋1=9。同样，十进制的6可写成0＋4＋2＋0，在二进制中表示为“0、1、1、0”。

只要我们比较一下十进制数与二进制数的进位关系，就可以明显的看出它们各自遵循的规律和它们之间的关系。十进制数是逢十进一，所以在任一数后面加上一个零，得到的数将是原来的数乘十。二进制数是逢二进一，所以在任一数后面加上一个零，得到的数是原来的数乘2。所以，二进制数中，数码“1”出现在第一位是1×2\(^{0}\)，出现在第二位“10”就表示 1×21，出现在第三位“100”就表示1×22，出现在第四位“1000”就表示l×2\(^{3}\)……，出现在n位

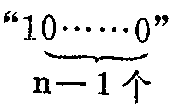
就表示1×2\(^{n}\)-1。这里也表明了二进制数转换成十进制数的方法，如：

至于十进制数转换成二进制数，可用“除二取余法”，即将十进制数除以2，一直到商数等于0为止，取其余数。例如把十进制数9化为二进制数：

这里还需注意一点，二进制数的0和1，表示的是数，而双稳态触发器的“0”和“1”，表示的是输出电位低和高两种状态，它们的含意是不同的。（天津市四十二中学 凌肇元）