从电容两端电压不能突然变化谈起
使用过万用表的同志都有这样的经验:当用万用表欧姆档测量较大容量电容时,刚一接上电容,表头指针摆动很大,然后再慢慢地退回来。这说明在万用表和电容构成的电路中,开始有一个很大的电流,然后逐渐减小。这个现象是由电容本身的特性——电容两端电压不能突然变化——决定的。
我们知道,电容具有存储电荷的能力,而且当容量为C的电容两极板带有一定量的电荷Q时,电容两端就出现相应的端电压U\(_{c}\)(Uc=\(\frac{Q}{C}\))。我们通常说的电容“充电”,就是指电容上电荷积累的过程,“放电”是电容上电荷释放的过程。
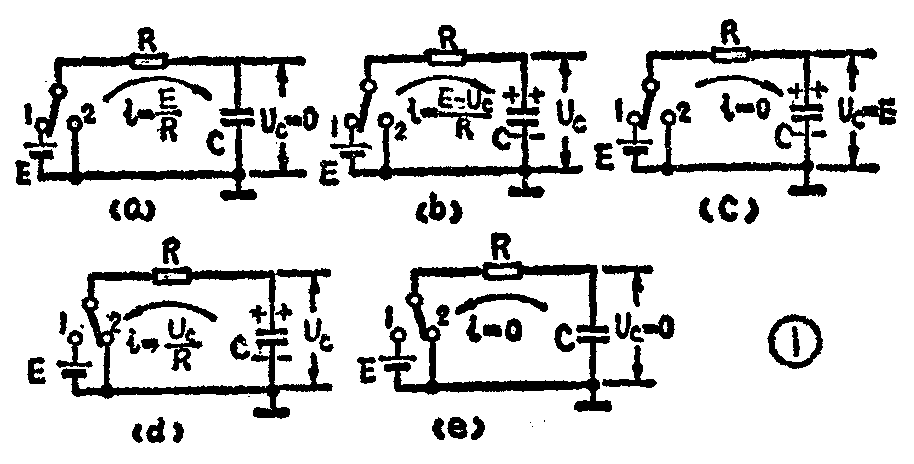
图1是描述电容充放电过程的实验电路。设没有充电前电容C上没有电荷,显然这时它的端电压也为零。在接通电源(开关拨到“1”)的瞬间,电容来不及积累电荷,端电压还等于零,而电路中的电流最大:i=\(\frac{E}{R}\)(见图1a)。随着时间的推移,电容上逐渐积累起电荷,端电压U\(_{c}\)也就相应地上升;Uc的极性正好和电源E相反,因此充电电流i=E-U\(_{c}\);R随Uc增大而逐渐减小(见图1b)。当电容充电到U\(_{c}\)等于E时,充电电流降为零(见图1c),充电过程就结束了。这也正是万用表测电容时发生的过程。
如果在某一瞬间把开关突然拨到“2”(见图1d),由于电容上的电荷来不及释放,在这一瞬间电容上的电压U\(_{c}\)仍保持开关拨到“2”之前的数值。然后,电容经过电阻R放电,放电电流i=UcR随着U\(_{c}\)的下降逐渐减小,直到电荷放完,Uc衰减到零为止,如图1e所示。
这个实验揭示了电容的重要特性:电容两端电压的建立(更确切地说,电压的增大和减小)是需要时间的,换句话说,电容两端的电压在任何时候都不能突然变化。这一点在脉冲技术中经常应用,要很好地理解。道理其实很简单,因为电容两端的电压是靠电容极板上的电荷维持的,电荷变化过程实际上是在电容两极板间电场的能量积累和释放过程,而能量的积累和释放都需要一定时间。
电容两端电压的建立需要一定时间,这个时间又是由什么决定呢?很明显,电容C越大,充电到同样电压需要积累的电荷越多,时间也就越长;电阻R越大,电路中充电电流越小,电容上电荷积累的过程也就进行得越慢。理论分析进一步证明,电容C和电阻R的乘积的大小决定着电容充放电过程的快慢。我们把τ=R·C叫做电路的时间常数,R和C的单位取欧姆和法拉时,τ的单位是秒。通常R和C的单位取千欧和微法(或微微法)、τ的单位是毫秒(或毫微秒)。
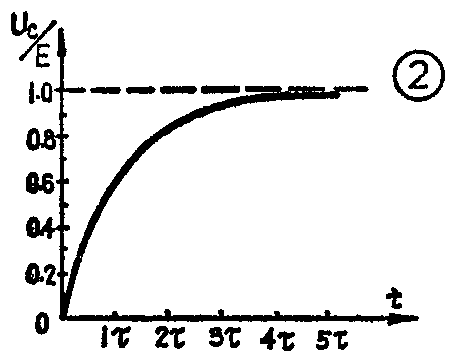
为了进一步说明电容充电过程快慢和充电时间常数τ的关系,下表中列出了以τ为单位的充电时间t和U\(_{c}\)与电源电压之比Uc/E的对应值。用图形表示就得到图2的曲线。这条曲线在数学上叫指数曲线,所以我们常说电容两端电压是按指纹规律随时间变化的。从表和图2中可以看出,就整个充电过程来说,τ越大,充电越慢;当t=3τ时,U\(_{c}\)/E=0.95,t=5τ时,Uc/E>0.99。一般认为充电时间t=(3~5)τ时,电容上电荷已经充满。

RC微分电路
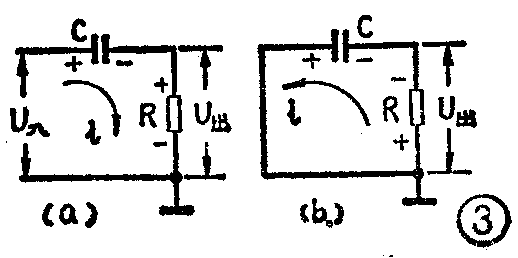
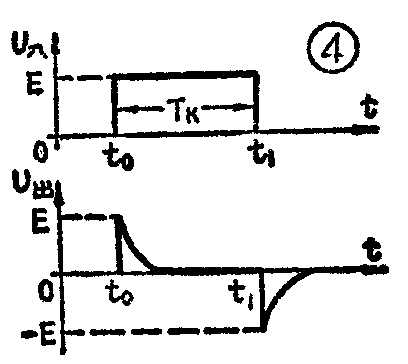
在图3a所示的电路中,如果时间常数τ远小于输入脉冲的宽度T\(_{k}\),就构成了RC微分电路。下面分析它的工作过程,参看图4。在t=t0时,U\(_{入}\)从零跳变到E,使电容左极板电位,从零跳变到E,由于电容上的电压不能突然变化,要维持Uc等于零,右极板电位必然也要从零跳变到E,输出端就产生了一个幅度为E的正跳变。在t\(_{0}\)<t<t1这段时间内,U\(_{入}\)=E,电容C通过电阻R按指数规律充电。因为τ=RC《Tk,同时U\(_{出}\)=UR=E-U\(_{C}\),所以充电过程很快完成,随Uc迅速充到E(左极板电位为E,右极板为零),U\(_{出}\)按指数规律迅速下降到零,结果在输出端形成了幅度为E的正尖脉冲。到t=t1时,U\(_{入}\)从E回跳到零,相当于电容左极板接地(图3b),同样由于电容两端电压不能突然变化,电容右极板电位将从零跳到-E,维持Uc仍然等于E。当t>t\(_{1}\)时,电容通过R放电,放电电流的方向及它在R上压降的极性见图3b。放电电流很快衰减到了零,在输出端便形成了幅度为E的负尖脉冲。由此可见,微分电路把输入矩形脉冲变换成了一正一负两个尖脉冲,突出了输入信号的变化部分(输入信号变化很快时,输出大),而把恒定部分压低到零(输入信号不变化时,输出为零),所以微分电路的特点可以说成是“突出变化量,压低恒定量”。
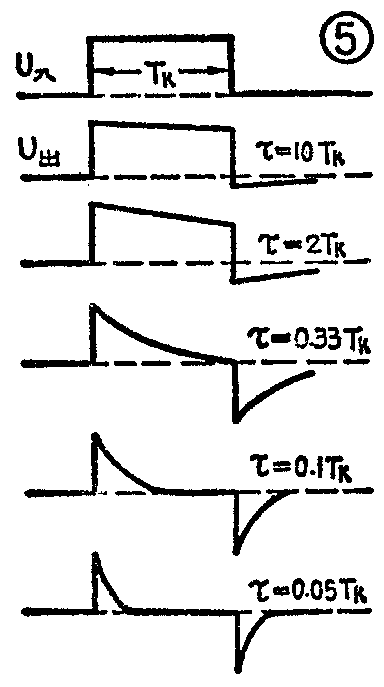
值得注意的是,图3电路中的时间常数τ必须小于(\(\frac{1}{3}\)~1;5)T\(_{k}\),才是微分电路。当RC过大,不满足上述条件时,电路就起不到微分作用了。时间常数对输出波形的影响见图5,显然,如果τ很大,例如τ=10Tk时,输出波形和输入波形就很相似,电路成为放大器中常见的RC耦合电路了。
RC微分电路用途很广,下面介绍两个例子:
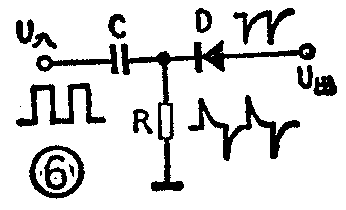
1.触发器的输入电路 双稳态或单稳态触发器的输入电路,通常由RC微分电路及选择脉冲极性的二极管D组成,如图6所示。微分电路把时钟脉冲变成尖脉冲,经二极管D只把正的或负的尖脉冲送到触发器。
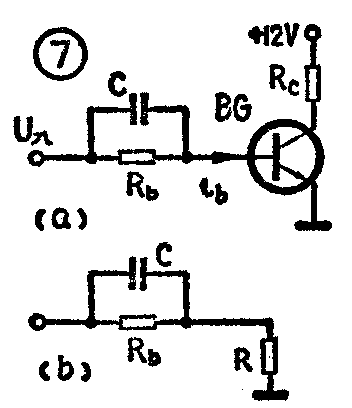
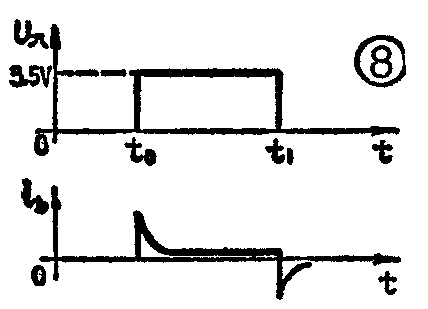
2.加速电路 为了提高三极管的开关速度,常采用电容加速电路,如图7a所示。图7b是它的等效电路,其中加速电容C和三极管输入阻抗R组成微分电路。设输入脉冲幅度为3.5伏。当U\(_{入}\)从零突然变到+3.5伏时,Uc不能突然变化,U\(_{b}\)也跳到+3.5伏,从而可提供比不接加速电容时大得多的正向基极电流,使管子很快导通,Ub=0.7伏。随后电容C充电,一直充到U\(_{c}\)=3.5伏-0.7伏=2.8伏。当U入从+3.5伏下跳到零伏时,U\(_{b}\)也要下跳3.5伏,即从+0.7伏下跳到0.7伏-3.5伏=-2.8伏,这就又提供了很大的反向基流,使管子迅速截止。总之,有了加速电容后,可以缩短三极管的开关时间(参看图8)。
RC积分电路
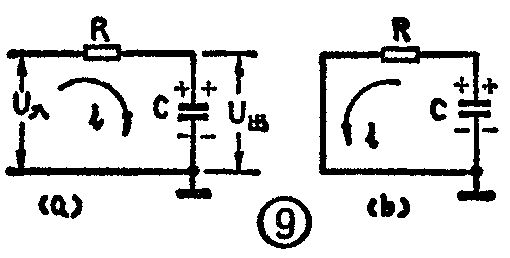
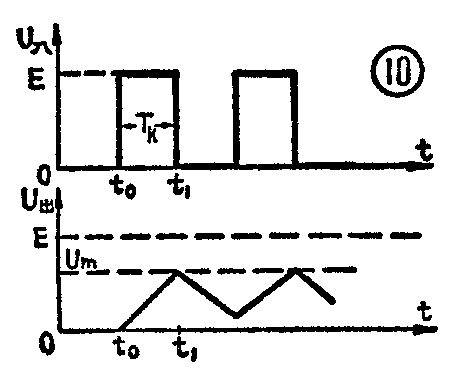
把微分电路中R和C的位置对调,并且使电路时间常数τ远大于输入脉冲宽度T\(_{k}\),就构成了RC积分电路,见图9a,其输入、输出波形示于图10中。电路工作过程的分析和微分电路相似。在t=t0时,U\(_{入}\)从零跳变到E,由于电容两端电压不能突然变化,U出=U\(_{c}\)=0。在t0<t<t\(_{1}\)这段时间内,电容两端电压按指数规律上升到Um。因为τ》T\(_{k}\),充电很缓慢,所以到t1时刻电容两端充得的电压很小,U\(_{m}\)<E;这段时间内Uc的变化仅是按指数规律变化的整个充电过程的一小段,可以近似看成直线。到t=t\(_{1}\)时,U入变为零,而U\(_{出}\)=Uc仍保持在U\(_{m}\)。t>t1时,电容C放电(图9b),放电时间常数还是τ=RC,也可以看成直线放电。这样,我们就在输出端得到了近似三角波的输出,幅度比输入脉冲小。显然,和微分电路相反,积分电路的特点是把输入信号的突然变化变换成为缓慢变化。而电路起积分作用的条件是τ=RC》T\(_{k}\)。
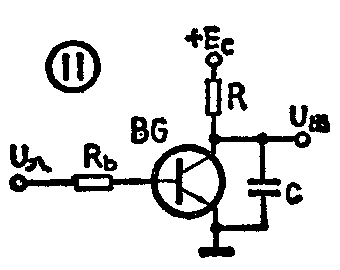
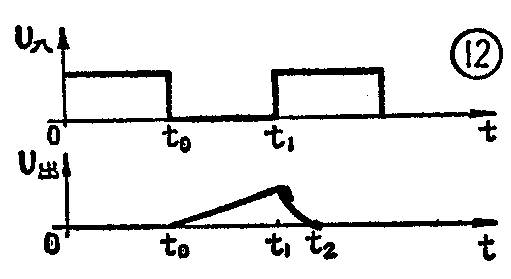
1.锯齿波发生器 RC积分电路在电视机、示波器中,用做产生随时间线性变化的电压的锯齿波发生器。图11是一个最简单的锯齿波发生器,输入、输出波形见图12。不难看出,在t<t\(_{0}\)时,U入=E,BG导通,U\(_{出}\)=Uc=0。在t\(_{0}\)<t<t1时间内,U\(_{入}\)=0,BG截止,电阻R和电容C起积分电路作用,+Ec通过R对C充电,充电曲线近似直线,从而形成锯齿波电压的正程(t\(_{0}\)~t1)。当t=t\(_{1}\)时,U入又从零跳到E,BG导通,这时C通过BG很小的内阻快速放电,U\(_{c}\)迅速衰减到零,形成锯齿波电压的回扫期(t1~t\(_{2}\))。
2.积分抗干扰电路
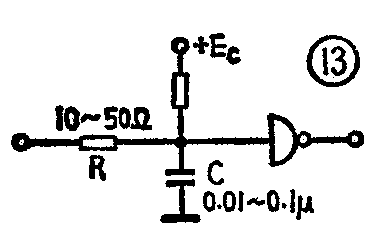
积分电路在电子设备中常用来抗干扰。如本刊今年第七期《步进式顺序控制器》(三)一文中曾介绍过,为增强组件抗干扰能力,可在接长联线的组件输人端加上积分抗干扰电路,如图13所示。其中R和C对干扰信号构成积分电路,把干扰脉冲的幅度压低,避免组件误触发。
几点体会
自然界是辩证法的宝库。遵照毛主席关于“要求大家逐步地学会使用辨证法这个科学方法”的教导,在学习微分电路和积分电路时,我们有下面几点体会:
1.刚接触脉冲技术的同志,往往以为在图1电路中,决定电容充电快慢的是电源电压E的大小,E越大,充电越快。事实并不是这样。“事物发展的根本原因,不是在事物的外部而是在事物的内部,在于事物内部的矛盾性。”如前所述,RC电路中,电容充放电的快慢是由R和C本身的大小决定的,τ=RC越大,充放电越慢;反之,充放电越快。那么,电源电压E的作用又是什么呢?“每一事物的运动都和它的周围其他事物互相联系着和互相影响着。”RC电路不接电源,电容不能充电;在电源电压不同时,电容两端充电到相同电压需要的时间也不同。但后一现象并不意味着电容充电快慢的改变,因为在不同电源电压下,电容充电到各自最大电压(即电源电压)用的时间是相同的;充电过程中,充电到各自最大电压相同百分数的时间也是相同的(τ就是电容充电到电源电压的大约百分之六十三时需要的时间,见前文附表)。总之,电源电压的大小只能影响充电过程中每瞬间电容电压的大小,而不能影响整个充电过程的快慢。
2.“对立统一规律是宇宙的根本规律。”RC微分电路和积分电路,都是利用电容器的充放电现象来达到波形变换的目的。输入脉冲期间,电容充电;输入脉冲结束后,电容放电。这是一对矛盾,推动着电路的运动和变化。为什么微分电路和积分电路的作用又有很大不同?这是因为“每一物质的运动形式所具有的特殊的本质,为它自己的特殊的矛盾所规定。微分电路中,τ《T\(_{k}\),充放电进行得很快,在输入脉冲期间,电容很快就完成了充电过程,输入信号大部分降在电容上。积分电路情况就不同了,电容充电缓慢,输入脉冲期间,输入信号大部分降在了电阻上。矛盾的特殊性,决定着电路性质的不同。我们分别从电阻和电容上取出输出信号,就达到不同的波形变换的目的。(龚文)