基本逻辑电路浅介

当我们打开一台电子计算机的机箱时，呈现在我们眼前的，是一排排印刷线路板上装着成千上万个电子器件和元件，一根根导线互相连接着，构成了一幅错综复杂的画面。乍看起来，似乎茫无头绪。但是，如果我们仔细研究，一点一点地剖析，就不难看出，这样一台机器尽管元器件多、线路复杂，却基本上都是大量相同电路的组合，基本电路形式不过只有几种。这几种基本电路，就是我们要介绍的基本逻辑电路。

所谓“逻辑”，是指一定的规律性；逻辑电路，就是按一定规律动作的开关电路。这种电路。一般具有几个输入端和一个输出端，当输入信号之间满足某一特定关系时，电路才有输出（开），否则没有输出（关）。这同生活中的开门和关门相似，所以又把逻辑电路叫做门电路。同时，逻辑电路的开和关两个状态，可以用二进制数中的“1”和“0”来表示，因此也叫做数字电路。

最基本的逻辑电路有三种：“与门”、“或门”和“非门”。它们分别执行三种基本逻辑功能：“与”、“或”和“非”。

在生产斗争、科学实验以及日常生活中，处处存在着“与”逻辑关系。我们以一台收音机的合格与否为例说明。大家知道，只有当收音机所有技术指标都合格时，这台机器才算正品；若有某一个或几个指标达不到规定要求，就不合格。设收音机主要技术指标有三个，即灵敏度、选择性、不失真功率，那么这种关系可以写成：

这就是“与”逻辑关系。写成逻辑关系式就是：

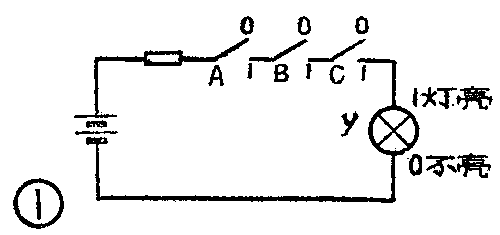
为了简明易懂起见，我们再举一个生活中的例子。图1线路中有三个串接着的开关A、B和C。显然灯和开关的状态之间存在着“与”逻辑关系，即：只有当A、B、C都合上时灯才亮；若有任一个或一个以上的开关没合上，灯就不亮。这里开关和灯都只有两种状态：合上或断开，灯亮或不亮。如果用“1”表示开关合上和灯亮，用“0”表示开关断开和灯不亮，“与”逻辑关系可以表达成：

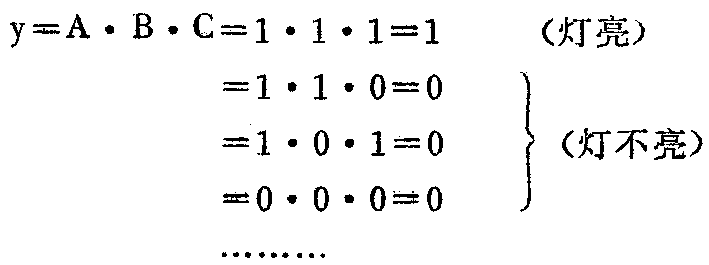
上面的例子说明，“与”逻辑关系的意义，是表示当各种条件同时具备时，才能得到某一结果。逻辑关系式中的符号“·”表示逻辑乘法运算。

实现“与”逻辑关系的电路称为与门电路。最简单的与门如图2（a）所示。它是有三个输入端的二极管与门，工作原理是这样的：设输入高电平为+V\(_{1}\)（V1＜V），低电平为0伏。当输入端A、B、C均为低电平时，三个二极管都导通，输出y为低电平；当输入端中有一个或两个为低电平时，相应的二极管由于两端电位差大优先导通，而使输入端为高电平的二极管处截止状态，输出y也为低电平；当三个输入端均为高电平时，三个二极管都导通，输出才为高电平。这就实现了“与”关系。由此看出，所以能实现“与”关系，是因为二极管处于正向导通状态时，其阳极电位和阴极电位相同（忽略二极管正向导通压降），具有箝制电位（箝位）——把电路中某点的电位固定在一定电平上——的作用。这里是把输出端y的电平箝位在输入高电平或低电平。在图2（a）电路中的几个二极管，阳极电位均高于阴极电位时，还有个电位差大的可以优先导通，y端电平被箝在电位差大的二极管输入电平上的特点。

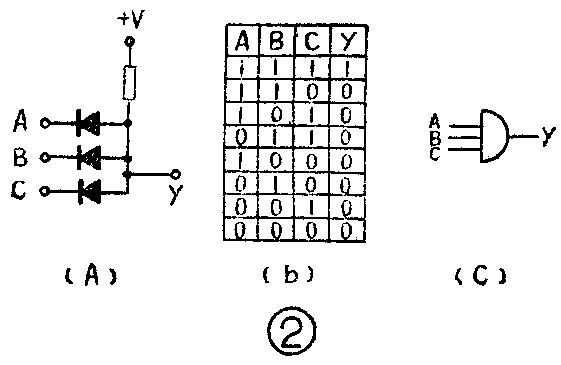
如果把输入电平和输出电平之间的关系列成表格，并用“1”表示高电平，“0”表示低电平，就构成了“真值表”，见图2（b）。与门逻辑符号示于图2（c）。

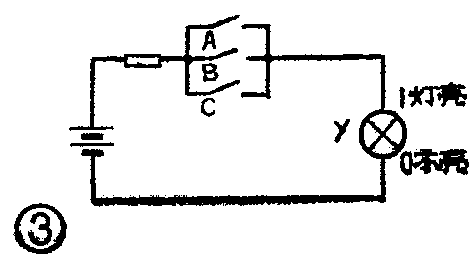
“或”逻辑关系也是我们经常碰到的。现仅以图3为例说明。三个并接的开关A、B、C中只要有任何一个或几个合上，灯就亮。这种关系可以写成：

开关A合上或开关B合上或开关C合上=灯y亮。

这就是“中”逻辑关系。仍然用“1”代表开关合上和灯亮，“0”表示开关断开和灯不亮，写成逻辑关系式为：

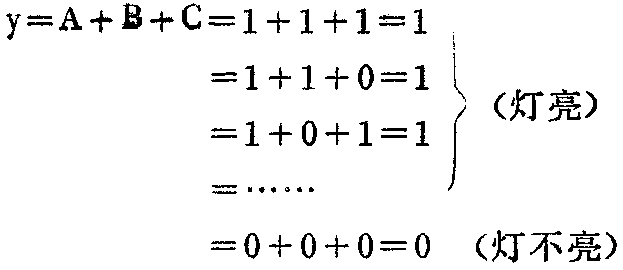
可见，“或”逻辑关系表示，在给定条件中只要有一个或一个以上条件具备时，就能得到某一结果。逻辑关系式中的符号“+”表示逻辑加法运算。要注意，这里1＋1=1，与算术加法不同。

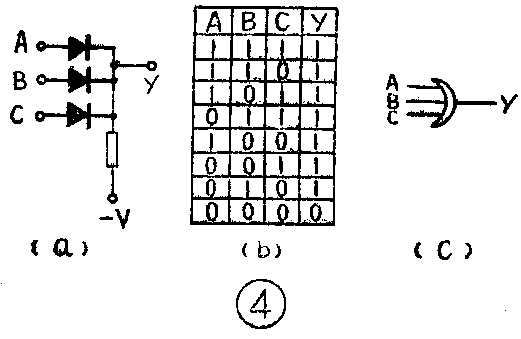
实现“或”逻辑关系的电路称为或门电路。最简单的二极管或门电路见图4（a），三个输入端A、B、C中只要有一个或一个以上的输入端是高电平（“1”），输出端y就是高电平（“1”），实现了“或”关系。或门电路真值表及逻辑符号见图4（b）、（c）。

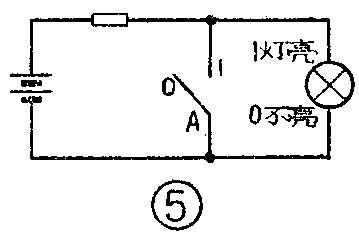
“非”逻辑关系表示否定或相反的意思。我们看图5，当开关A断开（“0”）时，灯亮（“1”）；开关A合上（“1”）时，灯不亮（“0”）。这就是说，条件和结果是相反的。若把量A的否定值用A-（读作A非）表示，使得到下面的逻辑关系式：

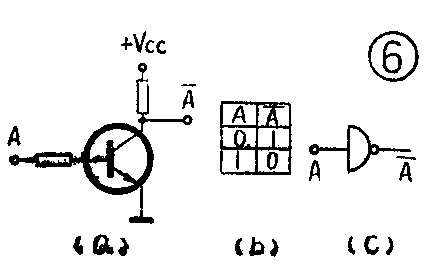
实现上述功能的电路叫非门电路。显然它只有一个输入端和一个输出端，而且输出总是输入的否定。晶体管反相器是最简单的非门电路，如图6（a）所示。根据三极管的开关特性，输入为低电平时，输出为高电平；反之，输入为高电平，输出则为低电平。非门电路的真值表和逻辑符号分别见图 6（b）、（c）。

上面介绍的三种门电路是最基本的逻辑电路。必须特别指出的是，一切事物都是相互联系和相互依赖的，矛盾的双方在一定条件下还可以互相转化。基本逻辑电路中的与门和或门也是这样。同一个电路，从不同角度考察它的逻辑功能，既可能是与门，又可能是或门。在前面的分析过程中，我们都是以高电平表示有信号，表示“1”的，称为“正逻辑”。如果恰恰反过来，以低电平表示有信号，表示“1”，就称为“负逻辑”。读者不难看出，正逻辑的与门，正是负逻辑的或门；正逻辑的或门，正是负逻辑的与门。在学习基本逻辑电路时，掌握这种辩证关系是很重要的。

在电子计算机和数字控制系统中，只有前面三种基本的逻辑电路是不够的，实际上常用的单元逻辑电路是上述三种电路的组合，即与非门、或非门和与或非门电路。随着半导体技术的不断发展和完善，半导体数字集成电路得到了广泛应用。下面就以应用比较普遍的TTL数字集成电路（晶体管——晶体管逻辑电路）和HTL数字集成电路（高抗干扰集成电路）为例，说明与非门和与或非门电路的逻辑功能。

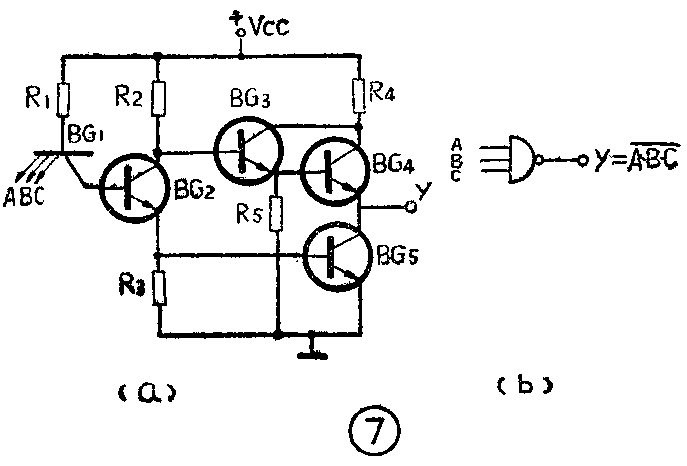
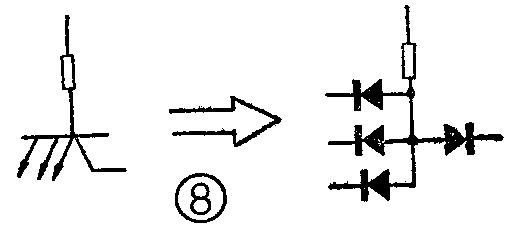
图7是TTL与非门电路。其中BG\(_{1}\)是一个多发射极晶体管（它的结构形式和普通晶体管相似，但有多个发射极），在一定意义下，可看作是一个与门和一个二极管串接在一起（见图8），它既有三极管的作用，又有二极管的作用，是TTL电路传输速度快的关键元件。当输入端A、B、C都是高电平时，BG\(_{1}\)的几个eb结都处于反向偏置，电源Vcc经过R\(_{1}\)和BG1的bc结向BG\(_{2}\)提供基极电流，使BG2导通。这时BG\(_{1}\)的bc结相当于一个正向二极管。BG2的发射极电流在R\(_{3}\)上产生的压降又使BG5导通。由于BG\(_{2}\)的集电极电位就是BG3的基极电位，BG\(_{2}\)导通时，BG2集电极电位为BG\(_{5}\)的eb结压降与BG2饱和压降之和，约为1伏，BG\(_{3}\)的基极电流使BG3刚刚进入导通状态，而不足以推动BG\(_{4}\)。这时，因为BG2和BG\(_{5}\)饱和，BG4截止，所以输出低电平。当输入端有一个或几个是低电平时，BG\(_{1}\)的eb结处于正向偏置了，BG1的基极电流不再流向BG\(_{1}\)集电极，而是流向发射极，因此BG2和BG\(_{5}\)都截止。BG2集电极电位接近电源电压V\(_{cc}\)，使BG3导通。BG\(_{3}\)发射极电流在R5 上的压降又使BG\(_{4}\)导通。BG4导通，BG\(_{5}\)截止，输出即为高电平。

综上所述，当输入端全为高电平时，输出为低电平；输入端中有一个或几个为低电平时，输出为高电平。这个电路具备了“与非”的逻辑功能。用逻辑关系式表达为：

与非门电路的逻辑符号如图7（b）所示。

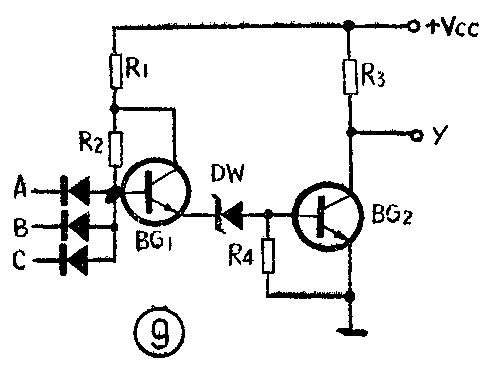
图9为HTL高抗干扰与非门电路。它的特点是使用了稳压二极管DW，抗干扰能力较强。由图9可见，当所有的输入端接高电平时，电流从电源V\(_{cc}\)经R1、R\(_{2}\)流向BG1基极，使BG\(_{1}\)导通。BG1发射极电位使DW进入击穿区，BG\(_{2}\)饱和，因此输出为低电平。而当有一个或几个输入端为低电平时，电流从电源Vcc经R\(_{1}\)、R2流向输入二极管到地，因而BG\(_{1}\)、DW和BG2均截止，输出为高电平。显然，从逻辑功能上看，HTL与非门和TTL与非门是一样的。只是由于DW的作用，在输入为低电平时，如果外来干扰信号不足以使BG\(_{1}\)基极电位升高到BG1、DW和BG\(_{2}\)均导通的，输出端仍为高电平，因而有较强的抗干扰能力。此外，电源电压也较HTL电路高，加大了输出的幅度，也有助于抗干扰能力的提高。

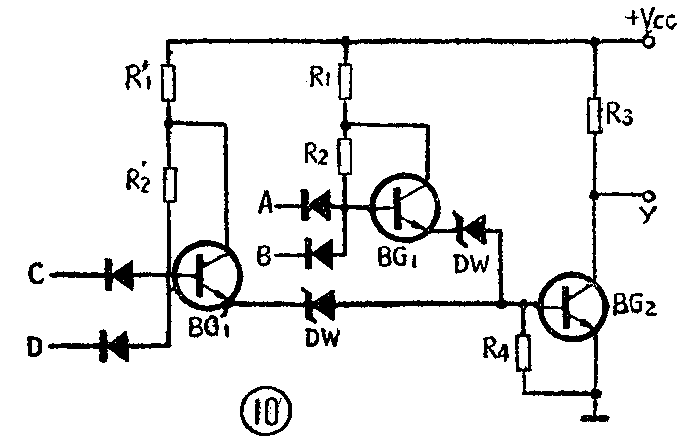
图10是HTL与或非门电路。把图9和图10比较一下，可以看到二者电路基本相仿，只是图10比图9多了一套输入二极管和BG1＇、DW＇等元件。正是把DW和DW＇都接到BG\(_{2}\)的基极上才构成了“或”的逻辑功能。当输入端A、B接高电平，C、D端接低电平时，BG1＇截止，BG\(_{1}\)导通，BG2也导通，输出低电平。只有当四个输入端A、B、C、D全都接低电平时，BG\(_{1}\)和BG＇1 均截止，BG\(_{2}\)也截止，输出才是高电平。其余各种输入状态，读者可自行分析。上述“与或非”的逻辑功能，可用逻辑关系式表达为：

过去，人们较多地使用与非门构成各种数字控制系统。由于与或非门可以简化逻辑设计，降低功耗，提高速度，目前用与或非门进行逻辑设计的日渐增多。

基本逻辑电路应用很广。我们可以用前面介绍的各种基本逻辑电路，构成各种通用电子计算机，去进行复杂的运算；构成各种专用计算机和数字控制装置，去指挥机床自动地进行加工和操作，控制轧钢机自动地进行生产……。在本刊介绍过的许多电子技术应用成果中，我们都可以看到基本逻辑电路的运用，本文就不再详细谈了。（黎辉宇）