我们工农兵学员,坚持“独立自主,自力更生”的方针,急工农兵所急,想工农兵所想。走出校门,到使用单位进行了调查研究。根据使用单位的需要,和便于普及的要求,同工人、教师、北京无线电三厂的同志一起,在MDJ—161Ⅰ型(其简介见《无线电技术》74年第1期)的基础上,将逻辑稍加变动,不增大体积,基本上采用原有的MOS集成电路片,改进了机器的性能。主要是增加了开平方、乘方、求平均值、百分比计算、X与Y交换、连乘除等功能;按一定操作顺序可解一元二次方程和三元一次联立方程。
在操作方面,为了符合使用习惯,把减法操作顺序作了更改。例如,7-5=2,原来的操作是:扑憬峁幌衷诘牟僮魇牵
92。
在显示方面,把没有意义的零均删去,不使它显示。例如:0.8800,取四位小数,原来的显示为:
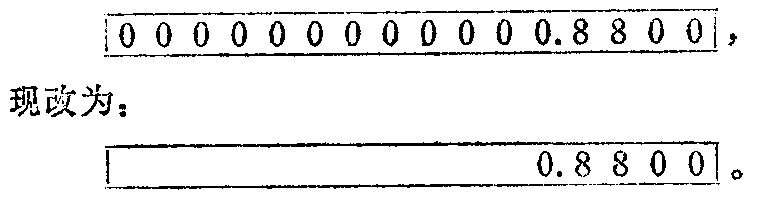
此外,还扩大了乘除法的运算容量。下面简单介绍一下开平方、求平均值、百分比计算以及删零的方法。
开平方:机器的开平方是总结了笔算开平方的方法,找出规律,运用等差级数的原理,通过机器作加减法来实现的。例如,计算\(\sqrt{3}\)=?
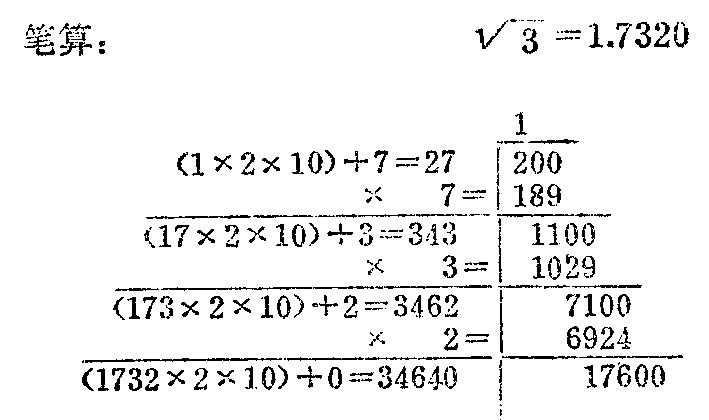
从笔算可以看出:(1)每一段的减数等于前面已开出方根乘2(设它为α)乘10,加上现开出的一位方根(设它为β),将其和与现开出的这一位方根β相乘之积。例如,第二段的减数是〔(1×2×10)+(7)〕×7=189。写成一般表达式为(α×10+β)β。
(2)全部开出的方根(例如1732,小数点不计在内)的2倍(3464),等于最后一位方根(2)的2倍(即2β),加上前面所得出的方根(173)乘2(即α),再乘10,即:3464=173×2×10+2×2,写成一般表达式为a×10+2β。
在计算机中,不能象人那样估算,只能按照预先规定的步骤一步一步地做。从笔算方法引伸出几点,即为计算机开方方法。
(1)据前所述,每一段的减数为(a×10+β)β,可将它展开为一个公差为2的等差级数和,其首项为(α×10+1),第二项为(α×10+1)+2,……第β项为(α×10+1)+(β-1)2=(α×10+2β-1),则β项的和为:
(α×10+1)+(α×10+3)+(α×10+5)+……+(α×10+2β-1)
=\(\frac{(α×10+1)+(2×10+2β-1)}{2}\)β
=(α×10+β)β
确定首项后,先从开方数减去首项,然后每次把减数加2再相减,直到不够减时,机器作出判断。
(2)假定是减了(β+1)次产生不够减的现象,那么把被减数恢复到β次的状态。(β+1)次提供的减数是(α×10+2β-1)+2=α×10+2β+1。如果不再往下开,则从减数中减去1,等于α×10+2β。对比笔算方法找出的第(2)点规律,它正好是全部开出的方根的2倍。把它除以2即得所求之方根。
(3)如果继续开下去,那么下一段的减数为前面已开出的方根的2倍乘10加1,由于(β+1)次提供的减数是α×10+2β+1,而前面已开出的方根的2倍是α×10+2β,所以继续开下去时,下一段的减数应为〔(β+1)次的减数-1〕×10+1,即(α×10+2β)×10+1。
现将上述计算机开方方法举例说明:
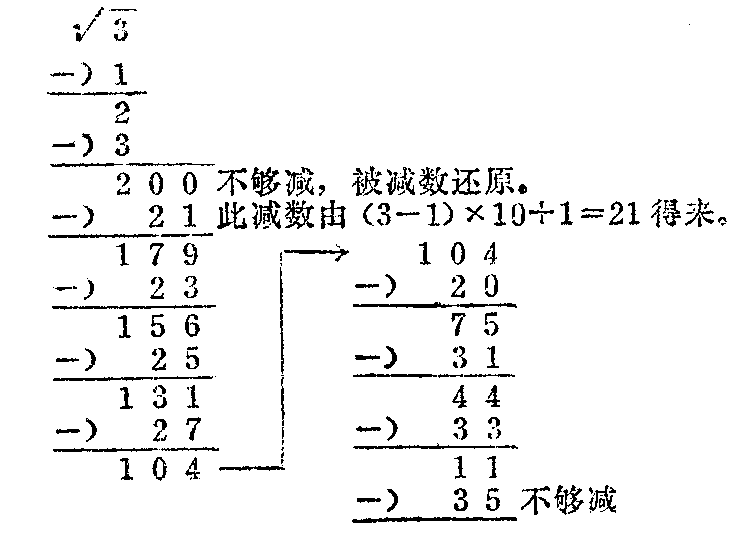
此时提供的减数35减去1等于34,除以2等于17,标出小数点为1.7,即所求之方根。还可以继续开下去,直至将寄存减数的移位寄存器的最低位填上数。
(4)方根小数点位置的确定:
该机字长是十进制16位。被开方数最多16位全是整数,开出的方根最多有8位是整数,如果要把机器的16位全填满,那么剩下的8位是小数,即小数点位置在第8位。这就是说,不论开什么数,开出小数至少是8位。如果被开方数是11位整数,5位小数;那么应开出6位整数,2位小数,方根小数点位置应从第8位再左移X/2=5/2(小数不计)=2位,即小数点位置在第10位。
求平均值方法:把累加的次数用4位(二进制)移位寄存器R记下来,最多记15次,每按一次键,R加1。累加和放在X寄存器,作为被除数。当按下求平均值键,R寄存器中的数作为除数送入X寄存器,被除数从X寄存器送入Y寄存器,随后自动进行除法,求得平均值。例如:
3451ㄆ骄担
百分比计算:例如求6是3的百分之几?操作步骤:7480(即6是3的200%)。又如,求6的3%是多少?94818(结果)。这两种情况都是在按时,使乘数或除数的小数点左移两位,除数由3变为0.03,则6÷0.03=200(%);乘数由3变为0.03,则6×0.03=0.18。
删零:它是通过两片32位显示扫描片和或门,控制荧光数码管栅极电压来实现的,使栅极只在有效数字对应的这几位扫描时间出现高电位。其余均为低电位,抑制电子,使其不能去撞击板极荧光粉,因而不能发光。
我们从学习MOS集成电路和动态逻辑,到完成MDJ—161Ⅱ型台式机的研制任务,仅用了短短四个月的时间,事实雄辩地证明了“七·二一”道路的无比正确和深远意义,这是对那些攻击工农兵上大学这一新生事物的反对派的有力回击。(清华大学电子系计04班台式机毕业实践小组工农兵学员)