为了使放大器合理地工作,必须给它设置适当的工作点,即选择一组合适的I\(_{b}\)、Ic和V\(_{ce}\)值。此外,由于晶体管的特性容易受温度的影响,当温度升高时,Iceo显著增加,而I\(_{c}\)=βIb+I\(_{ceo}\),所以Ic也随着增大,从而引起工作点的改变。因此,对放大器不仅要求能有适当的工作点,而且要求工作稳定。解决这些问题的电路,叫做直流偏置稳定电路,简称偏置电路。
固定偏置电路
这种电路见图1,是共发射极基本放大电路。如果E\(_{c}\)、Rb选定了,就能得到一个固定的偏流I\(_{b}\)和固定的Ic,所以叫做固定偏置电路。
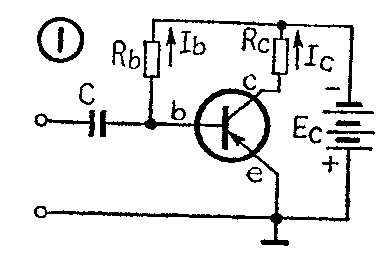
固定偏置电路,只能提供一个固定的偏流I\(_{b}\),不能起到补偿温度变化的影响的作用。它的优点是电路简单,所用零件较少。
一般情况下,E\(_{c}\)、Ic、R\(_{c}\)和β、Iceo等值都是预先根据放大器的工作要求确定了的。计算偏流I\(_{b}\)和偏流电阻Rb时,可利用以下公式:
I\(_{b}\)=Ec-V\(_{be}\)Rb……(1)
I\(_{c}\)=βIb+I\(_{ceo}\)……(2)
式中V\(_{be}\)是基极发射极之间的电压,由于加的是正向电压,Vbe数值很小(锗管一般为0.2伏左右,硅管一般为0.7伏左右),与E\(_{c}\)相比,可以忽略不计。所以
(1)式可化为I\(_{b}\)=EcR\(_{b}\)……(3)。
从(2)(3)两式,可算出I\(_{b}\)和Rb值。在实际应用时,还要调整R\(_{b}\),得出较精确的Ic值。调整R\(_{b}\)的方法见图2。根据计算得出的Rb数值,选择一个适当的电位器W和一个固定电阻R,接在电路中R\(_{b}\)的位置。在Rc上串接一个毫安表。变动电位器W,使电表读数为预定的I\(_{c}\)值。然后,测出这时电位器和固定电阻的串联总值,用一只阻值相同的固定电阻换入电路,就调整好了。与电位器W串接一个固定电阻,是为了防止调整中因偏流过大而烧坏管子。
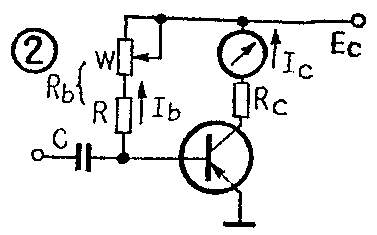
电压负反馈偏置电路
图3是一种电压负反馈偏置电路。与图1电路不同之处是将偏置电阻R\(_{b}\)接到了集电极c。从图3可以看出,ec间的电压,等于Veb加上R\(_{b}\)上的电压降IbR\(_{b}\),即
V\(_{ec}\)=Veb+I\(_{b}\)Rb。
同样,可以看出
E\(_{c}\)=Vec+I\(_{c}\)Rc。
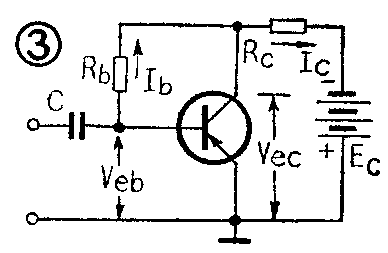
从上面两式,可以算出R\(_{b}\)=(Ec-I\(_{c}\)Rc-V\(_{eb}\))/Ib,由于V\(_{eb}\)很小,与Ec比可以忽略,并且I\(_{b}\)≈Ic/β,所以R\(_{b}\)≈(Ec-I\(_{c}\)Rc)β/I\(_{c}\)。
电路的负反馈过程是这样的:如果温度上升,引起I\(_{c}\)增大,那么电压降IcR\(_{c}\)也增加。由于Ec=V\(_{ec}\)+IcR\(_{c}\),Ec是电源电压,相对来说是不变的,所以I\(_{c}\)Rc增大后,V\(_{ec}\)必须减小,才能维持Ec=V\(_{ec}\)+IcR\(_{c}\)这个等式。另外,上面已说过,Vec=V\(_{eb}\)+IbR\(_{b}\),所以在Vec减小时要保持V\(_{ec}\)=Veb+I\(_{b}\)Rb,V\(_{eb}\)就必然减小。但是Veb减小,就减小了正向偏压,必然引起I\(_{b}\)下降,Ib下降必然引起I\(_{c}\)下降,这样又把Ic拉回来了,达到了温度补偿的目的。这个循环过程可写成:
温度↑→I\(_{c}\)↑→IcR\(_{c}\)↑→Vec↓→V\(_{eb}\)↓→Ib↓→I\(_{c}\)↓
显然,要使负反馈效果好,就要求R\(_{c}\)足够大,这样才能引起Vec的足够变化,使V\(_{eb}\)有足够的下降,降低Ib,拉回I\(_{c}\)。用变压器作负载的放大器,由于变压器线圈的直流电阻较小,不能满足Rc足够大的要求,所以不适合采用这种电压负反馈的偏置方法。由于R\(_{c}\)要求有较大的阻值,所以Rb不能太大,否则建立不起合适的工作点。R\(_{b}\)太小,则使VebV\(_{ec}\)过大过小,也建立不起合适的工作点。一般取Rb=(2~10)R\(_{c}\)。
电流负反馈偏置电路
这种电路如图4所示。与图1的区别,是在发射极e上串接了一个电阻R\(_{e}\)。
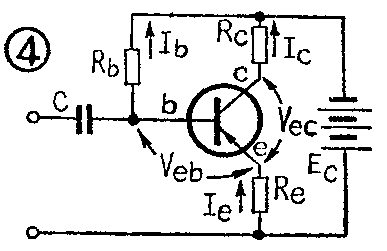
电路的负反馈过程是这样的:如果温度上升引起I\(_{c}\)增加,则发射极电流Ie也随着增加,使R\(_{e}\)上电压降IeR\(_{e}\)增加。从图4可以看出,Ec=I\(_{e}\)Re+V\(_{eb}\)+IbR\(_{b}\),Ec是电源电压,相对不变,所以I\(_{e}\)Re增加,必然引起V\(_{eb}\)下降,才能保持Ec=I\(_{e}\)Re+V\(_{eb}\)+IbR\(_{b}\)这个关系式。Veb下降,引起I\(_{b}\)下降,这样就把Ic拉回来,达到温度补偿的目的。这个过程可写成:
温度↑→I\(_{c}\)↑→Ie↑→I\(_{e}\)Re↑→V\(_{eb}\)↓→Ib↓→I\(_{c}\)↓
显然,R\(_{e}\)越大,压降IeR\(_{e}\)的变化就越大,负反馈越强。但是,R3不能太大,否则在同样的E\(_{c}\)下,会使Vec降低太多,降低输出。一般取I\(_{e}\)Re≤1伏即可。这时R\(_{e}\)的数值为Rc的1/10~1/5。
典型的偏置电路
这种电路如图5所示,是最常用的偏置电路。它有下列两个稳定作用:
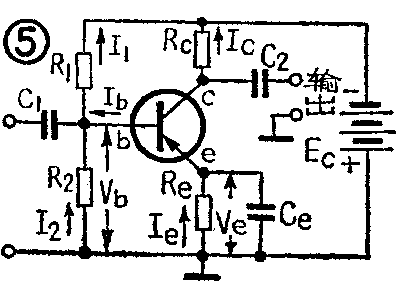
1.通过基极电阻R\(_{1}\)和R2的分压关系,在I\(_{b}\)与I2相比可忽略不计的条件下,可使基极电压V\(_{b}\)基本上固定(从图5中可看出,如果忽略Ib,那末I\(_{2}\)=I1+I\(_{b}\)=I1,V\(_{b}\)=Ec-I\(_{1}\)R1,V\(_{b}\)=I2R\(_{2}\),从这三个式子,可算出Vb=E\(_{c}\)R2/(R\(_{1}\)+R2),说明V\(_{b}\)只受Ec、R\(_{1}\)、R2的影响,只要E\(_{c}\)、R1、R\(_{2}\)确定,Vb就可保持固定)。
2.接入了R\(_{e}\),所以有电流负反馈的补偿作用。如果Vb比V\(_{be}\)大很多,那末Ie=\(\frac{V}{_{b}}\)-VbeRe≈V\(_{b}\);Re。因此,V\(_{b}\)固定后, Ie也就相对固定。I\(_{e}\)能固定,Ie就可与晶体管的参数变化和温度变化几乎无关。
这种电路除了稳定作用较好以外,还有一个优点是R\(_{c}\)值取得小些也不影响稳定性,因此适合各种负载。
现在以图5电路为例,介绍低频小信号放大器的简易计算方法。
1.选择晶体管:一般低频小信号放大器对管子的要求不高,I\(_{ceo}\)不超过100μA(微安)、β在20至100间的管子都可以用。
2.电源电压E\(_{c}\):不能超过晶体管的击穿电压,一般在4.5伏到18伏等数值中选用。
3.集电极电流I\(_{c}\):可在0.5~2mA(毫安)间选择,功放级可用到3~10毫安。Ic小些可减少功率损耗和噪声,但I\(_{c}\)大小,会使β值显著减小。Ic的最大值不能超过管子的最大允许电流I\(_{CM}\)。
4.管压降V\(_{ce}\):一般可选在Ec的\(\frac{1}{2}\)~2;3范围内。V\(_{ce}\)太小,管子可能工作于饱和区;Vce太大,会降低电压放大倍数。
5.发射极反馈电阻R\(_{e}\):一般取Ve≤1伏即可。确定I\(_{c}\)后,可按Re≈\(\frac{V}{_{e}}\)Ic计算。
6.分压电阻R\(_{1}\)、R2:上面说过,希望I\(_{2}\)远大于Ib,所以要R\(_{1}\)R2小。但I\(_{2}\)越大,在R1R\(_{2}\)上损耗的功率也越大,对输入交流信号的旁路作用也增大,降低了输入信号。所以R1R\(_{2}\)要适当考虑,一般取I2≈10I\(_{b}\)就可以了(硅管可以更小些)。I2确定后,根据V\(_{b}\)≈Ve,不难求出
R\(_{2}\)≈VbI\(_{2}\)≈Ve;I\(_{2}\)≈IcR\(_{e}\)I2,
R\(_{1}\)≈Ec-V\(_{b}\)I2=E\(_{c}\);Ic-R\(_{2}\)。
7.集电极负载电阻R\(_{c}\):Rc大,则电压放大倍数高,但R\(_{c}\)上损耗也加大,而且容易产生失真。Rc太小,不但放大倍数降低,而且管子可能过负载而烧坏。一般选在几百欧到5千欧范围内。
8.电容C\(_{1}\)、C2、C\(_{e}\):选用几十微法至几百微法的电解电容器,要求耐压数值稍高于电源电压。
例如,电源电压选为12伏,管子的β=60,I\(_{c}\)选为1毫安(0.001安),Vce选为6伏。按上述计算方法可计算出图5中各个电阻和电容的数值:
1.取V\(_{e}\)为0.7伏,则
R\(_{e}\)=0.7(伏)1(毫安)=0.7(伏);0.001(安)=700欧,取标称值680欧。
2.R\(_{c}\)=Ec-V\(_{ce}\)-VeI\(_{c}\)=12-6-0.7;0.001=5300欧=5.3千欧,取标称值5.1千欧。
3.I\(_{b}\)≈Icβ=1(毫安);60=0.016毫安=16微安。
4.I\(_{2}\)≈10Ib=10×16=160微安=0.16毫安。
5.R\(_{2}\)=VbI\(_{2}\)=IcR\(_{e}\);I2=1(毫安)×700(欧)0.16(毫安)=4200欧=4.2千欧,取标称值4.7千欧。
6.R\(_{1}\)=EcI\(_{2}\)-R2=12(伏);0.16(毫安)-4.2(千欧)=70.8千欧,取标称值68千欧。
7.C\(_{e}\)取50微法,C1、C\(_{2}\)取10微法。
——金编