双稳态触发器

双稳态触发器（双稳态电路）是一种能够实现脉冲记忆作用的基本脉冲电路。在计算技术、程序控制中获得广泛应用。

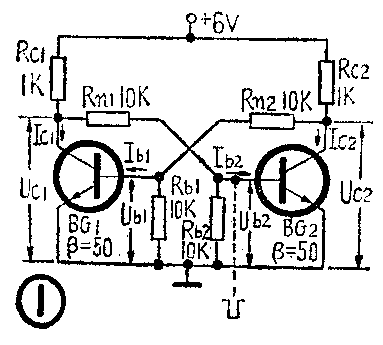
最简单的无偏压双稳态触发器电路如图①所示，是由两个反相器组成的环形电路。它为什么能够记忆脉冲呢？“事物发展的根本原因，不是在事物的外部而是在事物的内部，在于事物内部的矛盾性。”当电源接通后，假设一开始I\(_{C1}\)=IC2。但存在于同一事物中的矛盾的双方（这里是BG\(_{1}\)和BG2），它们的平衡是暂时的，斗争是绝对的。电路中噪声干扰或元件误差都可能使某一管I\(_{C}\)增加。如IC2增加，则电路中发生如下的正反馈过程：

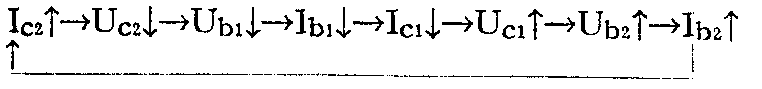
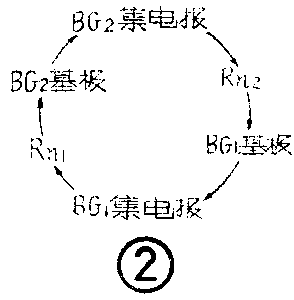
产生正反馈是因为电路中存在“再生环”，见图②。只要环中BG\(_{1}\)、BG2工作在特性曲线放大区，正反馈就不断进行下去，直到I\(_{C2}\)增大到使BG2工作点进入了饱和区。BG\(_{2}\)的饱和使Uc2降到0.35伏左右，经R\(_{n2}\)、Rb1分压后，U\(_{b1}\)必小于0.35伏而保证了BG1的截止（硅管工作在放大区时U\(_{eb}\)≈0.6-0.7伏）。电路便处于BG1截止、BG\(_{2}\)饱和的稳定状态。同样地，若电源接通瞬间BG1导电较强，在正反馈作用下，触发器将稳定于BG\(_{1}\)饱和、BG2截止的状态。

不难看出，上述两种稳定状态中，一管的截止或饱和是和另一管的饱和或截止互为依存的。只要电源电压保持稳定，元件不出故障，也没有太大的干扰时。触发器就能保持某一稳定状态不变。

“事情不是矛盾双方互相依存就完了，更重要的，还在于矛盾着的事物的互相转化。”在某一稳定状态下，若在饱和管基极引入一负脉冲，使其工作点重新移入放大区时，在再生环作用下，会发生电流电压变化与形成这一稳定状态时恰好相反的正反馈过程，最终使饱和管截止，截止管饱和，触发器由一种稳定状态翻转为另一种稳定状态。这种把脉冲引入电路使之翻转的方法称为“触发”。

正是双稳态触发器这种具有两种稳定状态，并且在一定信号触发下可以翻转的特性，成为它记忆脉冲作用的内因或根据。我们只要设法把需要记忆的脉冲一个个地依次触发双稳态触发器，使电路不停而可靠地翻转，便可记忆脉冲的个数了。

要准确可靠地记忆脉冲，电路必须有良好的稳定性，在干扰脉冲作用下不会引起误触发。图①所示的触发器中，截止管的U\(_{be}\)总是大于零的，与导通电压相差很小，当电路受到干扰时，导通管只要一退出饱和区，集电极电位略有上升，就很容易使截止管的Ube上升到0.7伏，而使电路翻转。这说明无偏压双稳态触发器的稳定性是不够好的。

为提高触发器的稳定性，要求加大导通管的饱和深度，使干扰脉冲到达时不易退出饱和区，同时要加大截止管的截止深度。减小R\(_{n1}\)、Rn2和增加R\(_{b1}\)、Rb2，可以使导通管深度饱和；但这样做又使截止管U\(_{be}\)抬高了。要从根本上解决问题，可采用图③的有偏压双稳态触发器。它和图①主要不同点是Rb1、R\(_{b2}\)由直接接地改接到-6伏偏压电源上了。图③中，Rn1、R\(_{n2}\)的数值比图①小， Rb1、R\(_{b2}\)数值比图①大，所以在使用相同晶体管的情况下，导通管饱和度加深。另一方面，用电阻分压器计算公式可以验证，由于偏压作用，截止管的Ube此时为-0.9伏，离开导通值有1.5-1.6伏的差值。这样必须有更大的干扰脉冲才能使导通管退出饱和及截止管导通，大大提高了触发器的抗干扰能力。

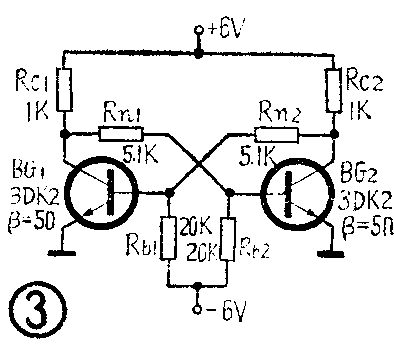
截止管基极对发射极的反偏置电压的数值是不是越大越好呢？不是的。因为，一方面过大的反偏置电压会损坏晶体管；另一方面，反偏置电压增大，导致触发脉冲的幅度也必须增大，电路的触发灵敏度就降低了。由此可见，抗干扰能力和灵敏度是互相矛盾的，必须统筹兼顾。

为了用双稳态触发器记忆脉冲，要求每当出现一个要记忆的脉冲时，触发器的状态就翻转一欢。怎样才能做到这一点呢？

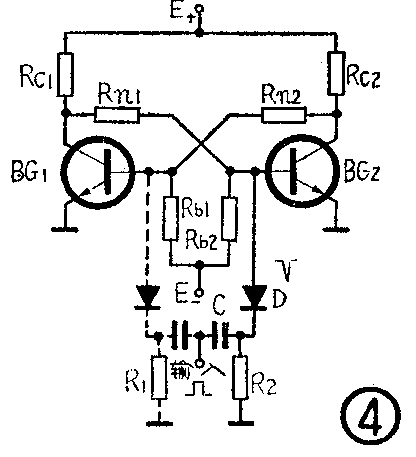
我们先来分析图④的电路。假设一开始触发器处于BG\(_{1}\)截止、BG2导通的状态。当有一方波信号输入时，经过R\(_{2}\)、C组成的微分电路和二极管D（它们一同构成了触发器输入电路），BG2基极便出现一个负向的尖脉冲，使触发器翻转，BG\(_{1}\)导通，BG2截止。第二个需记忆的方波信号输入时，BG\(_{2}\)基极又出现一个负向尖脉冲。但这时由于BG2已处于截止状态，输入的脉冲只能使它截止得更深，而决不会使触发器翻转（以后再有触发信号输入，触发器仍不能翻转）。为了使得在第二个触发信号到来时，触发器有可能翻转，我们首先会想到要在BG\(_{1}\)的基极上也接入一个触发器输入电路，并把两个输入端连在一起，如图④虚线所示。我们说这样做电路有可能翻转，是因为负脉冲同时加于两管的基极，使两管都截止。当负脉冲消失后，两管均有从截止转向导通的可能，无法保证原来截止的管子首先导通。因此会出现输入一个负脉冲后触发器不改变原来稳态的情况，破坏了计数的正常进行。

为了解决这个矛盾，就得使触发负脉冲依次轮流加入触发器导通管基极而不加到截止管基极。图⑤的电路可实现这一要求。它利用了触发器的内在性质和二极管单向导电特性。与图④不同处在于R\(_{1}\)、R2的接地端改接到BG\(_{1}\)、BG2的集电极了。设BG\(_{1}\)截止，Ub1＝－1伏，U\(_{c1}\)＝6伏； BG2导通，U\(_{b2}\)=0.7伏，Uc2=0.35伏。由于U\(_{c1}\)＞Ub1，所以A\(_{1}\)点电位为6伏，D1反向偏置；而U\(_{c2}\)＜Ub2\(_{2}\)点电位约为零点几伏，使D2处于正向导通或接近导通的状态。触发信号经微分后，峰值为±6伏的尖脉冲同时出现于A\(_{1}\)2点上。负极性脉冲出现时，A\(_{1}\)点电位等于零，因Ub1=－1伏，D\(_{1}\)仍反向偏置，负脉冲不能加到截止管BG1基极。但这时A\(_{2}\)点电位约为-5.65伏，D2正向偏置，于是负脉冲被引导到导通管BG\(_{2}\)的基极，完成一次翻转。下一个负脉冲则被引到BG1的基极。至于正脉冲，由于它将使A\(_{1}\)点电位上升为12伏，A2点电位为6.35伏，D\(_{1}\)、D2均反向偏置，因而无法引入BG\(_{1}\)、BG2的基极，于是双稳态触发器便能在需要记忆的脉冲触发下一来一回地翻转了。图⑤所示的这种触发输入电路称为“引导电路”。

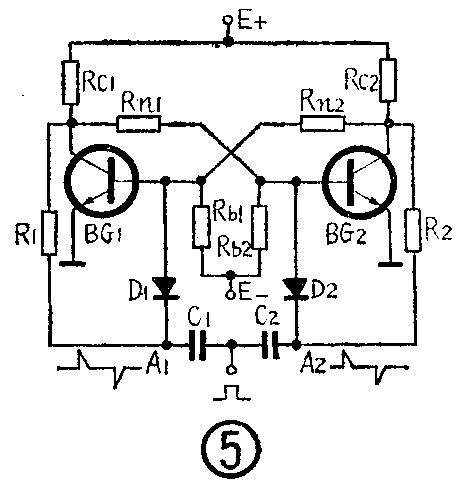
必须指出，如果加到A\(_{1}\)2点的负脉冲幅度太大，会使截止管的导引二极管处于正向偏置（如前例中幅度超过-7伏时），破坏了导引作用。所以对输入脉冲幅度应有一定限制，这同时也起到保护晶体管的作用。

由于双稳态触发器有两种稳定状态，人们很自然地把它和二进制数联系起来。如把图⑤中BG\(_{1}\)截止、BG2导通的状态做为二进制的“0”，把BG\(_{1}\)导通、BG2截止的状态做为二进制的“1”，可以得到下面的表：

忽略触发器电路的详细结构，而仅仅注意它和二进制数的关系，可以用图⑥（A）的简图来表示。图中Q-端表示从BG\(_{1}\)集电极引出，Q端表示从BG2集电极引出，CP端表示计数脉冲的输入端。

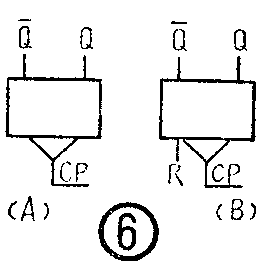
如果以Q-端或Q端有无高电位输出作为衡量标准，双稳态触发器的“0”状态，对应的是Q-端有输出，所以又把Q-端称为“0”输出端，简称“0”端；而Q端简称为“1”端，如下表所示：

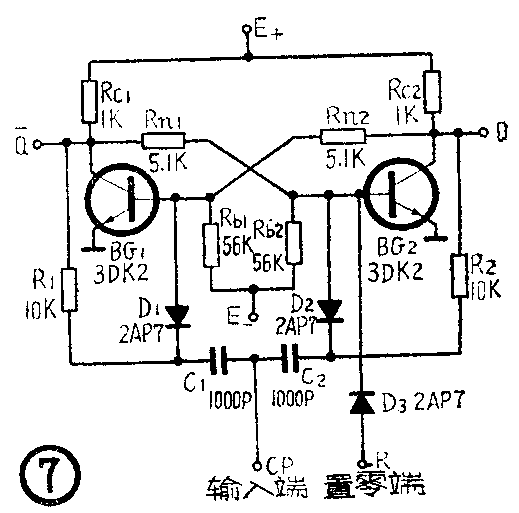
到此为止的分析中，我们忽略了下面这样一个问题：在刚接入电源的瞬间，双稳态触发器取那一种稳态是带有偶然性的，换句话说，一开始触发器究竟输出“0”还是“1”是不定的。这会给记数带来错误。为了解决这个问题，通常要加一个置“0”电路，如图⑦中所示。图⑦是某晶体管测频计数器中采用的双稳态触发器电路。置“0”电路由接在BG\(_{2}\)基极上的二极管D3组成。接上电源后，首先通过置零端加给BG\(_{2}\)一正脉冲，使BG2导通，BG\(_{1}\)截止，触发器就置于“0”状态了。置零端通常用R表示。图⑦电路的简化表示法见图⑥（B）。（上海少年宫科技组）