电阻应变片可以用来测量工程结构内部或机器部件等受力时所发生的各种应变。这种应变片是把纤细的电阻丝(直径为0.02~0.05毫米)粘贴在薄薄的绝缘底基上制成的。把应变片用特种胶水牢牢地贴在待试部件上。由于电阻丝底基和胶水都很薄,所以当试件受力而伸缩时,电阻丝也随着伸缩,它的长度、截面积和电阻率也随着变化。这样,应变片的电阻值就随着机器部件的变形而成比例地变化。通过电子仪器,就可显示或记录机器的变形。利用上述原理,应变片可用来测量各种机器部件的变形、应力、负荷,从而确定机器的能力和寿命,以便充分发挥机器的潜在能力,预防事故。应变片还广泛用在测量力、重量、压力、速度、加速度、弯矩、扭矩、振动、温度、应力分布、位移等。这些参数用一般测量装置很难精确测出,而用应变片就可以准确迅速测出,并能测得这些参数随时间而变化的关系。利用应变片还可以进行遥测和自动控制,可以在机器运转时进行现场测量,以显示或记录运行过程的状态;而且可以在高温或水下测量。如果用几个应变片放在部件的各个不同部分,还可以对各点同时进行测量。由于应变片体积小、重量轻,丝毫不影响机器工作,所以测量精度高,成为工业生产、设计、科学研究的一种重要的测量元件。
种类和构造
常见的应变片有以下几种。
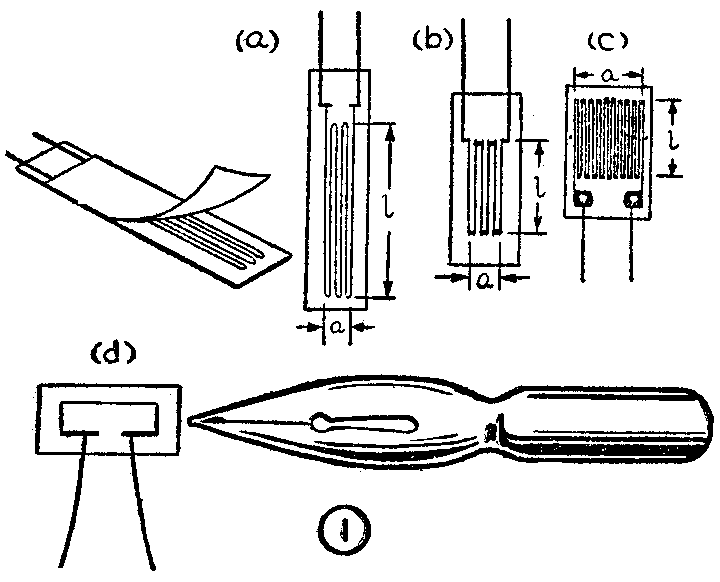
1.纸基丝绕式。外形如图1,a所示。它是把电阻丝(由康铜或镍铬合金丝制成)弯成栅状,用丙酮赛璐璐胶水粘贴在绝缘纸底基上,并在上面复一层纸制成。这种应变片适于在常温下使用,性能比较稳定,电阻值准确,粘贴简便,成本低廉。
2.胶膜短接线式。外形如图1,b所示。它是以聚乙烯醇缩醛胶(即БФ—2胶)做的薄膜为底基,各段电阻丝的两端分别用较粗的铜线连接起来。这种应变片受横向变形的影响小,测量精度高,性能稳定,寿命长。
3.箔式。外形如图1,c所示。它以高强度绝缘漆为底基,以康铜箔作电阻元件。可以通较大电流,可以大大简化测量仪器,横向效应小,寿命长。
4.半导体应变片。外形如图1,d所示。它是用含有导电物质(碳黑、石墨)、粘合剂(树脂)和填料(滑石、石英)的半导体作成薄带或细丝,再贴在绝缘纸上而做成的。这种应变片的体积小、灵敏度高,可测出微小的变形,输出信号大,可以使测量仪器简化,因而是很有发展前途的。目前这种应变片的缺点是阻值受温度变化的影响较大,不够稳定。
5.电阻应变花。又称电阻应变片丛,是把几个电阻应变丝,成一定角度贴在底基上制成的。弯曲的栅丝簇拥在一起,好象盛开的花朵。利用应变花可以测出应力分布情况。应变花各电阻元件间角度准确,保证测量精度,使用方便。各种应变花如图2所示。
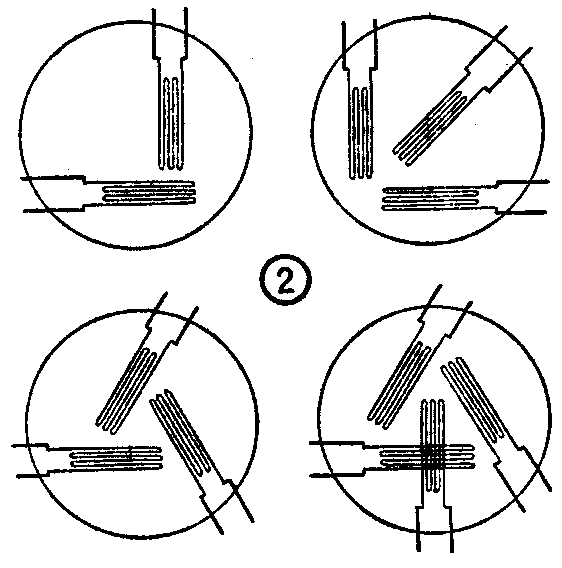
规格和参数
根据所要测量零件的大小来选用应变片的规格。应变片的主要规格尺寸是线栅宽a和基长l,如图1中所示。应变片规格就用a×l表示,如a=3毫米,l=15毫米,则表示为3×15。各种应变片有不同规格,以满足不同需要。
应变片的主要参数有:
1.电阻值。每个应变片的电阻值,最常用的是120欧姆,也有60,350欧姆的。
2.允许电流。纸基丝绕式和胶膜短接线式应变片的允许电流为20毫安左右,箔式应变片约为200毫安。
3.应变灵敏系数。把应变片贴在被试零件上,它的阻值就随试件的变形而变化。设电阻丝的总长为l\(_{0}\),总电阻为R0,在变形时总长度变化了Δl,总电阻变化了ΔR。实验证明,当电阻应变片受力变形时,电阻值的相对变化\(\frac{ΔR}{R}\)\(_{0}\),与此电阻丝的相对变化Δl;l0成正比,即
比例系数K称为应变灵敏系数,它取决于电阻丝的合金成分和加工工艺。K越大,就表示应变片越灵敏。一般应变片的K值在1.5~3之间。半导体应变片的K值可达100~200。
测量电路
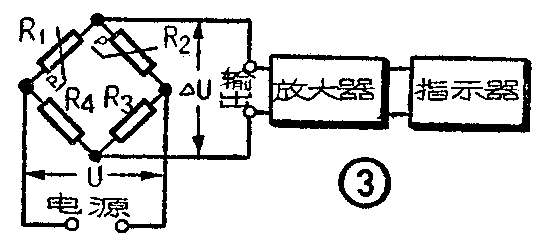
用应变片测量时,一般都接成桥式电路,如图3所示。其中R\(_{1}\)和R2是两个相同的电阻应变片,其中一个(例如R\(_{1}\))贴在被试零件上,而另外一个(例如R2)则不贴在零件上面,但这两个应变片都处在同样的温度条件下。这样,由于周围温度变化而引起的电阻变化,对两个电阻应变片来说是一样的,从而在测量线路中相互补偿,减小了由于温度变化而引起的测量误差。在试件未变形时,调节R\(_{3}\)、R4,使得
电桥平衡,输出ΔU=O。当试件受外力而变形时,R\(_{1}\)阻值变化了ΔR,电桥即有输出,其电压大小为
ΔU=\(\frac{1}{4}\)UΔR;R=\(\frac{1}{4}\)UKΔl;l。
因为式中供电电压U是固定的,K是常数,所以ΔU和\(\frac{Δl}{l}\)成正比。这就是说,材料变形越大,输出电压越大,所以电桥的作用就是把机械量输换成电量。输出电压可经过放大器加以放大,然后用指示器(例如毫安表或微安表)指示出来。
如果R\(_{1}\)、R2、R\(_{3}\)、R4都用相同的电阻应变片,而把R\(_{1}\)、R3贴在零件同一地方,使它们的变化大小相同,方向一致,那么,输出电压就可以增加一倍,即
ΔU=\(\frac{1}{2}\)UΔR;R
图3只适用于静态测量。若需作动态测量,例如测量零件的振动情况,则可用图4,a的动态测量电路。图中的电桥由超声频振荡器供电。在R\(_{1}\)未变形的情况下,通过电位器R6把电桥调得有某种程度的不平衡。这时,电桥有某一输出,在示波器上得到的波形如图4,b中的t\(_{1}\)段内所示,其幅度为A。当零件受到伸张时,电桥更不平衡,输出更大,示波器上所得波形的幅度增大到B(图中t2段)。相反地,当零件受到压缩时,电桥趋于平衡,输出减小,示波器上输出波形的幅度减小到C(图中t\(_{3}\)段)。伸张和压缩的数值分别由(B—A)和(A—C)来确定。因此,零件受力伸缩随时间变化的情况,就可以在示波器上显示出来。
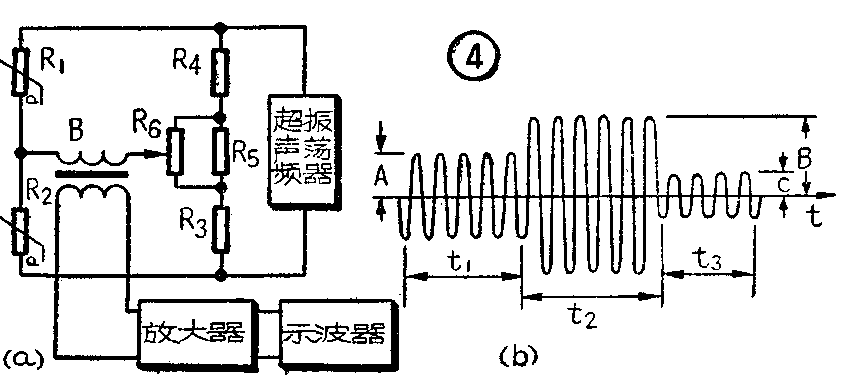
应当注意,在初始调节时,幅度A应调得足够大,以适应所需的测量范围。(电工)