半导体三极管放大电路与电子管放大电路有许多相对应之处,但也有许多与电子管电路不同的特点。通常电子管是电压控制元件,而半导体三极管是电流控制元件。基于这一重要区别,在实际应用中,半导体管电路的耦合方式比电子管更多。本文介绍的复合半导体三极管,就是半导体管的一种特殊耦合方式。
什么是复合半导体三极管?
两个半导体三极管如图1a那样直接连接起来就可构成一个复合半导体三极管。对外电路来说,这一结构与单一半导体管(简称单一管)一样,有基极、发射极和集电极,可当做一个三极管来用(图1b)。BG\(_{1}\)的发射极电流即是BG2的基极电流,总基极电流是BG\(_{1}\)的基极电流,总发射极电流为BG2的发射极电流,总集电极电流为BG\(_{1}\)与BG2的集电极电流之和。
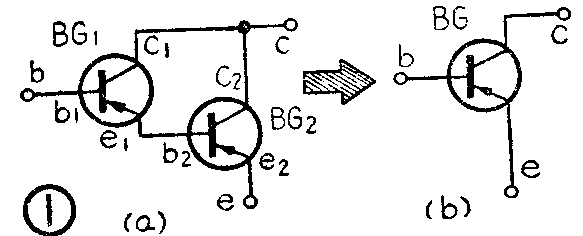
复合起来的半导体三极管具有许多单一管所没有的特性,用它可构成高输入阻抗放大器、电流增益高的带通放大器,等等。在这里,我们介绍这种复合管的一些特性供读者参考。为了叙述方便起见,下面把构成这种复合管的普通半导体管称为构成管。
复合管的电流放大系数
首先讨论复合管的共基极电流放大系数。根据定义,半导体三极管的共基极电流放大系数(请参阅本刊1964年第11期“半导体三极管的基本电路和特性参数”一文)
式中ΔI\(_{c}\)为集电极电流变化量,ΔIe为发射极电流变化量(以下BG\(_{1}\)、BG2两管各极电流分别以下标1、2表明)。
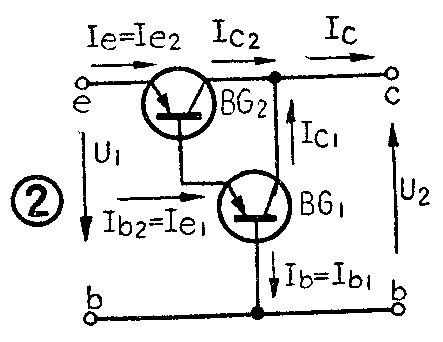
在图2中,设构成管BG\(_{1}\),BG2的共基极放大系数为α\(_{1}\),α2,则有
α\(_{1}\)=ΔIc1ΔI\(_{e1}\)=ΔIc1;ΔI\(_{b2}\)
α\(_{2}\)=ΔIc2ΔI\(_{e2}\)=ΔIc2;ΔI\(_{e}\)
而复合管的共基极电流放大系数为
α=\(\frac{ΔI}{_{c}}\)ΔIe
因为ΔI\(_{c}\)=ΔIc1+ΔI\(_{c2}\),ΔIe2=ΔI\(_{b2}\)+ΔIc2
及ΔI\(_{e1}\)=ΔIb2=(1-α\(_{2}\))ΔIe2
=(1-α\(_{2}\))ΔIe
α=\(\frac{ΔI}{_{c}}\)ΔIe=ΔI\(_{c1}\)+ΔIc2;ΔI\(_{e}\)
=\(\frac{ΔI}{_{c2}}\)ΔIe2+ΔI\(_{c1}\);ΔIe2
=α\(_{2}\)+(1-α2)\(\frac{ΔI}{_{c1}}\)ΔIe1
=c\(_{2}\)+α1(1-α\(_{2}\))
所以复合管的共基极电流放大系数为
α=α\(_{1}\)+α2-α\(_{1}\)α2 (1)
从上式可以得出下列简要结论:
第一,复合管的共基极电流放大系数非常接近于1。例如,设构成复合管的两个面结合型低频管的α\(_{1}\)=α2=0.96,则复合管的α,按式(1)为0.998。目前还难以制造α值如此近于1的面结合型低频管。
第二、复合管的α极为稳定。当外界条件使构成管的α\(_{1}\)及α2有较大变化时,复合管的α仅作微小变动。例如,BG\(_{1}\)及BG2的共基极电流放大系数同时从0.96降为0.90时,则由公式(1)知,α仅从0.998降为0.99。前者的相对变化达6.2%,而后者仅为0.8%。显然复合管要稳定得多。
第三、复合管的共基极截止频率f\(_{α}\)比其构成管要高。当输入构成管的信号频率达到它的截止频率fα1时,BG\(_{1}\)与BG2的α值降为低频时的1\(\sqrt{2}\),即0.96;2=0.681(从上述),而这时复合管的α,按公式(1),为0.898。要使α降为低频时的1\(\sqrt{2}\)即0.998;2=0.70,与之相应的α\(_{1}\)=α2=0.45,远比0.681为小,对应于此值的运用频率f\(_{α}\)显然比fα1要高得多。复合管f\(_{a}\)的提高,对于常用低频管来说是很有意义的。从图3可以看出这一关系。
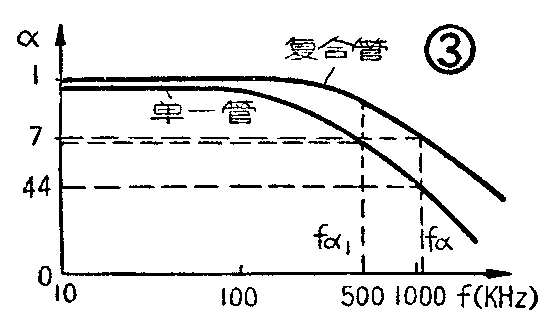
现在再看一看复合管的共发射极电流放大系数。此系数的定义是
β=\(\frac{ΔI}{_{c}}\)ΔIb。
(参阅本刊1964年第11期“半导体三极管的基本电路和特性参数”一文)
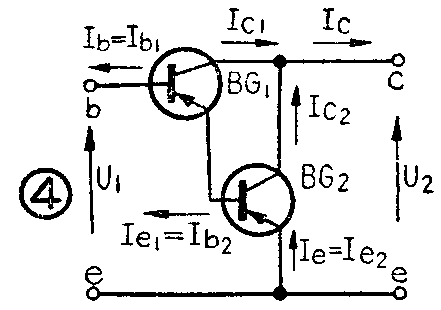
在图4中,设BG\(_{1}\)与BG2的共发射极电流放大系数分别为β\(_{1}\)与β2,则有
β\(_{1}\)=ΔIc1ΔI\(_{b1}\),β2=ΔI\(_{c2}\);ΔIb2
而复合管的
β=\(\frac{ΔI}{_{c}}\)ΔIb=ΔI\(_{c1}\);ΔIb1+\(\frac{ΔI}{_{c2}}\)ΔIb2
从图4知ΔI\(_{b}\)=ΔIc11+β\(_{1}\)
代入前式,便得复合管的共发射极电流放大系数为
β=β\(_{1}\)+β2(1+β\(_{1}\))
=β\(_{1}\)+β2+β\(_{1}\)β2 (2)
通常β\(_{1}\)、β2远比1为大,因而有
β≈β\(_{1}\)β2 (3)
由公式(2)或(3)可以看出:
第一,复合管的共发射极电流放大系数比单一管要高得多。仍以前述α\(_{1}\)=α2=0.96的构成管为例,它们的
β\(_{1}\)=β2=0.961-0.96=24>>1。
按公式(3)计算,复合管的β≈600,远较β\(_{1}\)=24为大。事实上,也还难以制造具有β值这样大的半导体管。
第二,复合管β值的稳定性较差。从公式(3)可知,当β\(_{1}\)及β2各有1%的相对变化时,β约有2%的相对变化。
第三,复合管的共发射极通频带比其构成管为窄。因为当输入信号频率提高时,β\(_{1}\)与β2还没有降到低频时的1/\(\sqrt{2}\)以前,复合管的β已降为低频时的1/2了。从公式(3)可以看出,此时β\(_{1}\)与β2的值,约为其低频值的\(\sqrt{1}\)/2≈1/1.2,显然与此值相对应的频率f\(_{β}\)比fβ1要小一些。对于一般的低频音频放大来说,其频带的变窄是有限的,截止频率仍在音频范围之外,故影响不大。
共集电极接法的电流放大系数与共发射极接法的相同。
输入阻抗
1.共基极接法的输入阻抗 在图2中,设构成管BG\(_{1}\)及BG2的共基极输入电阻分别为R\(_{sr1}\)及Rsr2,则输入信号电压变化量ΔU\(_{1}\)=Rsr2ΔI\(_{e}\)+Rsr1(1-α\(_{2}\))ΔIe,因此,复合管的共基极输入电阻为
R\(_{sr}\)=ΔU1ΔI\(_{e}\)=Rsr2+(1-α\(_{2}\))Rsr1
通常α\(_{2}\)≈1,故Rsr≈R\(_{sr2}\),即复合管的共基极输入阻抗与单一管的相近而稍大,一般为几十欧左右。
2.共发射极接法的输入阻抗 设构成管的共发射极输入阻抗为R\(_{sr1}\)与Rsr2,根据图4可有ΔU\(_{1}\)=(Rsr1ΔI\(_{b}\)+Rsr2ΔI\(_{b2}\)),因为ΔIb2=(1+β\(_{1}\))ΔIb,故得复合管的共发射极输入阻抗为
R\(_{sr}\)=Rsr1+(1+β\(_{1}\))Rsr2
一般β\(_{1}\)远比1大,因而Rsr≈β\(_{1}\)Rsr2,即复合管的输入阻抗比单一管的约大β\(_{1}\)倍。通常Rsr2为几百欧到千欧左右,根据β\(_{1}\)值的不同,复合管的Rsr可从几千欧到几十千欧。复合管共发射极输入阻抗的增大,消除了单一管输入阻抗小的困难,有利于它在电路中的直接连接,并可避免对于电路其它部分(例如检波器)的不良影响。
3.复合管的共集电极电路 用共集电极复合管构成的发射极输出器的电路示于图5。通常单一管半导体电路的输入阻抗总是较小,即使是接成共集电极电路也不能提高很多,远较电子管电路为低,对外电路有不良影响。复合管的共集电极电路则能克服这一困难,并且具有极低的输出阻抗。
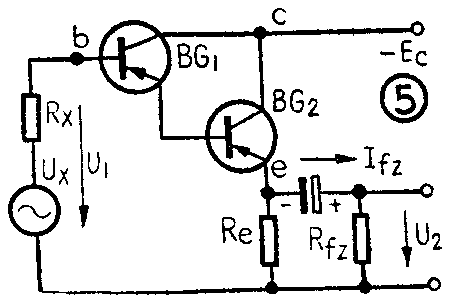
如图5所示,复合管发射极输出器的输出端阻抗基本上是R\(_{e}\)与Rfz的并联值,记为R\(_{o}\)。用Rsr1与R\(_{sr2}\)分别表示BG1及BG\(_{2}\)的共发射极输入阻抗时,复合管的输入阻抗即为Rsr=\(\frac{ΔU}{_{1}}\)ΔIb=R\(_{sr1}\)+(1+β1)R\(_{sr2}\)+(1+β1)(1+β\(_{2}\))Ro
设β\(_{1}\)=β2,当R\(_{o}\)在几百欧以上时可得
R\(_{sr}\)≈(1+β1)\(^{2}\)R\(_{o}\)
单一管共集电极电路的输入阻抗约为(1+β\(_{1}\))Ro,显然复合管要比它大得多,实际上可达几百千欧到兆欧数量级,这样高的输入阻抗,可与电子管电路的相比,是单一半导体管电路所不能实现的。(全为民)