在许多电子仪器和测量仪表里常常用到电桥电路。为了知道电桥负载的工作状况,例如要求得负载上的电压、电流及电桥的灵敏度等。必须进行复杂的运算。为了避免这种复杂的运算,这里设计了专门用来解算电桥的诺模图。
如图所示,电桥的两臂是R\(_{1}\)、R2及R\(_{3}\)、R4,电源为E。
根据网路理论,可把这个电桥看作一个有源二端网路。它的两个输出端为A及B。这样,A、B两端左侧的电路就可以用一个具有内阻R\(_{i}\)的等效电势E0来简单地代替。于是,电桥的工作情况就可以通过由E\(_{0}\)、Ri串联的简单电路而得到。
本文介绍的谐模图就是专门用来计算等效电势E\(_{0}\)及等效内阻Ri的。下面通过一个具体例子来说明它的用法。
设R\(_{1}\)=8 R2=2 R\(_{3}\)=4
R\(_{4}\)=5电源E=4.5这里各阻值的单位可以任取,如欧、十欧、百欧、千欧等均可。也可为2欧、3欧、4欧……等任定的单位,只是要求各阻值应取同一个单位。同样电源E的单位也是可以任取的。
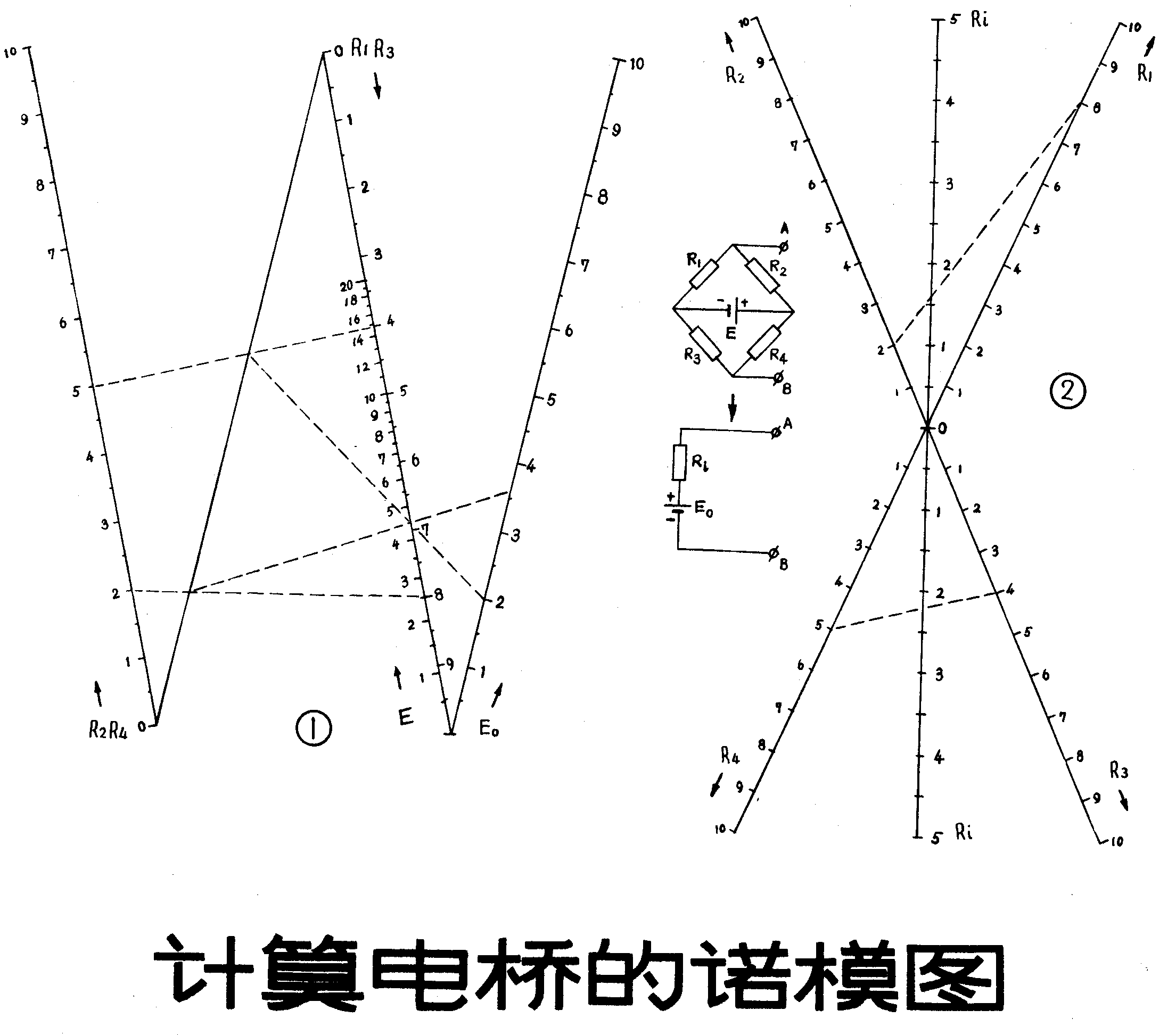
(一)用图1求等效电势E\(_{0}\)
(1)在R\(_{1}\)、R3尺上取R\(_{1}\)=8 R3=4,在R\(_{2}\)、R4尺上取R\(_{2}\)=2 R4=5,在E尺上取E=4.5。
(2)联接R\(_{1}\)、R2及R\(_{3}\)、R4,在辅助线上先后得两个交点。
(3)将此二交点按得到的先后次序与E=4.5点联线,先后在E\(_{0}\)尺上得到的二交点之差值即为所求之等效电势E0=1.6。
(二)用图2求等效内阻R\(_{i}\)
(1)在图中各尺上分别取得对应之R\(_{1}\)、R2、R\(_{3}\)、R4。
(2)联接R\(_{1}\),R2及R\(_{3}\),R4,在R\(_{i}\)尺上截取之长度即为所求之Ri= 3.8。