间接调频的方法

间接调频，就是先对高频振荡进行相位调制，然后再设法把调相振荡转变为调频振荡。怎样调相？又是怎样能由调相转变为调频呢？让我们先来研究一下调相振荡的特点。

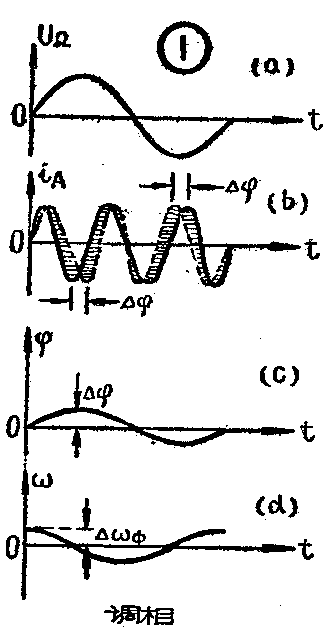
图1中绘出了高频振荡相位被调制时的情况。图la是用来调制高频振荡的音频信号电压U\(_{Ω}\)。图1b是高频振荡电流和被调相后的电流ia波形。其中虚线是未调制前的高频振荡电流，当它的相位受到音频信号调制后就得到如图1b中实线所示的调相振荡电流波形。它的相位是随着调制电压U\(_{Ω}\)的振幅而变化的。在这个例子中，当调制信号为正半周时，ia的相位超前，调制信号为负半周时，i\(_{a}\)的相位滞后。而相位超前和滞后的程度也是随着调制信号电压的大小而变化的。当调制信号电压逐渐增大时，调相电流的相移也逐渐增大，当调制电压逐渐减小时，调相电流的相移也逐渐减小，当调制电压达到峰值时，调相电流的相移最大，称为“最大相移”，或“调制指数”，用△{示。图1c中绘出了调相时高频电流的相位调制信号而变化的情况，可以看出，它是随调制电压成正比地变化的，调制电压的振幅愈大，最大相移也就越大。这点和调频振荡的“频偏”与调制电压振幅成正比是相似的。另外在上一期中介绍调频振荡的特点时，曾经提到，振荡的频率和相位是互相有联系的，频率的变化，必然伴随着相位的变化。调频振荡除了频率变化外也有相位的变化。同样，调相振荡也存在着频率的变化，如图1d所示。其频率变化的最大值就是调相时的频偏，图中用△ωφ表示。由此可见，调相波和调频波的性质是很相似的。它们所不同的是：当调制电压的振幅不变而频率改变时，调频振荡的“频偏”不变，而调相振荡的频偏△ω\(_{φ}\)却随调制频率成正比地变化。这是因为，当调制电压的振幅不变但频率升高时，调相振荡的相位化率加快，结果使频偏△ωφ。随调制频率的上升而增大；反之，频偏将减小。因此，利用调相振荡来传输时，就必须将设备的通频带按最高调制频率来考虑，这样，设备在一般调制频率下工作时，频带宽度不但没有被充分利用，反而会增加干扰杂音串入的机会。所以在实际应用中，调相振荡没有被广泛地应用，通常都用调频方式来传输。如果能够使调相振荡的频偏不随调制信号的频率而变化，就具有和调频振荡相似的性质，即由调相转变为调频了。间接调频法就是根据这个原理而实现的。

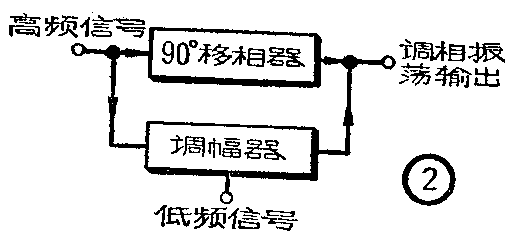
用已调幅的高频信号和一个经过固定移相的高频信号相加，就能够获得调相振荡。图2就是这种调相电路的方框图。高频信号是由频率比较稳定的晶体振荡器产生的，它被送到调幅器中被音频信号调幅，同时，又通过一个固定的90°移相器进行移相，移相后的高频信号与已调幅的信号直接相加，即可获得调相振荡输出。

要了解调相的过程，让我们先看看两个不同相位的高频振荡相加时的情况。图3（a）绘出两个频率和幅度相同但相位相差90°的高频电压u\(_{1}\)和u2，以及它们直接相加后所得到的合成电压u。

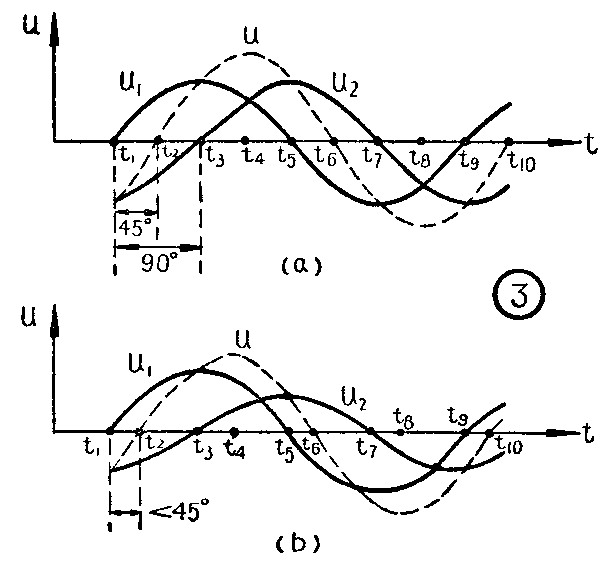
这两个电压相加时的一些特殊点是，当时间为t\(_{1}\)、t5、t\(_{9}\)的瞬刻，电压ul为零，故合成电压u等于u\(_{2}\)的瞬时值。在t2、t\(_{6}\)、t10时，u\(_{1}\)与u2的瞬时值相等，但极性相反，所以u等于零。在t\(_{3}\)、t7时，u\(_{2}\)为零，则u等于u1。在t\(_{4}\)、t8时，合成电压最大，u在t\(_{4}\)时为正最大值，而在t8时为负最大值。其他时间的u值则根据u\(_{1}\)与u2的瞬时值直接相加，其结果如图所示。

由图3（a）可看出，当把两个相位相差90°的高频电压直接相加时，所得到的合成电压u的相位将落后于u\(_{1}\)45°。并且，u的幅度也比单独的u1或u\(_{2}\)大。如果把u1的幅度固定而将u\(_{2}\)减小，则合成电压的情况如图3（b）所示。由图可见，电压ul等于u\(_{2}\) 而极性相反的点t2、t\(_{6}\)、t10将因u\(_{2}\)的减小而向左移动，其他合成点亦相应地往左移。于是合成电压落后于ul的相位就小于45°。如果u\(_{1}\)固定，而改变u2的大小时，合成电压落后于u\(_{1}\)的相位亦将随之改变。因此，如果我们对两个相位相差90°的高频电压中的一个进行幅度控制，就可获得相位变化的高频电压输出。

图4就是根据以上原理实现相位调制的电路。当电子管屏极回路调谐到和加在栅极上的高频电压的频率相同时，回路表现为纯电阻特性。屏极回路上包含有两个高频电流。一个是高频电压U\(_{g}\)经极间电容Cag在屏极回路上产生的电流I\(_{1}\)，由于Cag较小，它的电抗较大，所以I\(_{1}\)的性质主要决定于Cag而为容性电流，其相位超前于U\(_{g}\)90°。因为屏极回路呈现为电阻性，I1在回路上的高频电压降与I\(_{1}\)同相而超前于Ug90°，此电压相当于图3里的u\(_{1}\)。另一电流Ia是电子管受高频电压U\(_{g}\)激励而产生的高频电流，它与Ug同相。因此，I\(_{a}\)在屏极回路上的电压降将与Ug同相而落后于u\(_{1}\)90°，此电压相当于图3里的u2。

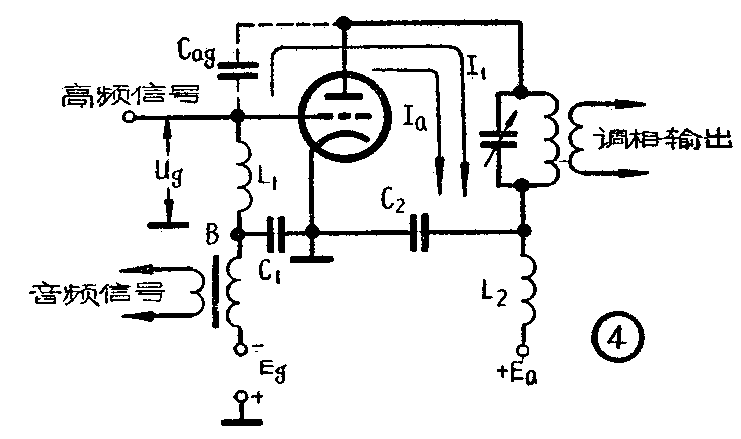
由于采用了栅极调幅电路，电流I\(_{a}\)将随着从变压器B送到栅极上的音频电压变化，这样，屏极回路上由Ia所产生的高频电压u\(_{2}\)的幅度亦将随音频电压改变。而电流I1在调幅过程中是不变的，故u\(_{1}\)的幅度并不改变。因此，在屏极回路上所得到的合成高频电压的相位将随着u2幅度的变化而改变，也就是由幅度调制转变成为相位调制。

从图3（b）还可以看出，已调相的电压u除了相位变化外，它的幅度也是变化的。这种现象称为寄生调幅，在实用上必须设法消除。因此，采用图5所示的双管调相电路要比单管电路好些。在双管电路中，电子管A和B的屏极并联接到公共的谐振回路，选择栅极上的电阻R和电容C的值，使C的电抗与R的电阻相等，则加于电子管A和B栅极上的高频激励电压的相位相差90°。这样，屏极回路上两个电子管的电流I\(_{A}\)和IB的相位也相差90°，此两电流所产生的高频电压就相当于图3里的u\(_{l}\)和u2。

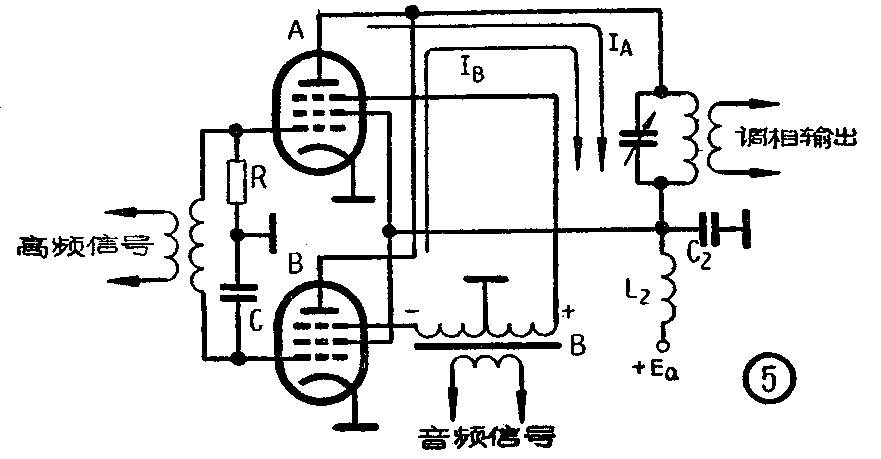
电子管A和B采用了反相的抑制栅极调幅电路，音频电压经变压器B反相加于两管的抑制栅极。当音频电压使A管电流I\(_{A}\)增加时，则B管的电流IB将减小，即回路上的高频电压u\(_{l}\)和u2的大小随音频电压作相反方向的变化。于是合成电压的相位亦随之改变，适当地选择两管栅极高频激励电压的大小，这种调相电路的寄生调幅是不大的。

实验表明，上述第一种调相电路不可能产生大于45。的相位调制。而第二种电路由于电压u\(_{l}\)和u2的大小同时变动，因而获得较大的相位变动，其最大相位移动为±45°。但是在实用上由于相位调制角度过大时，将使信号产生很大的失真，因此，通常都调变在±14°以内。

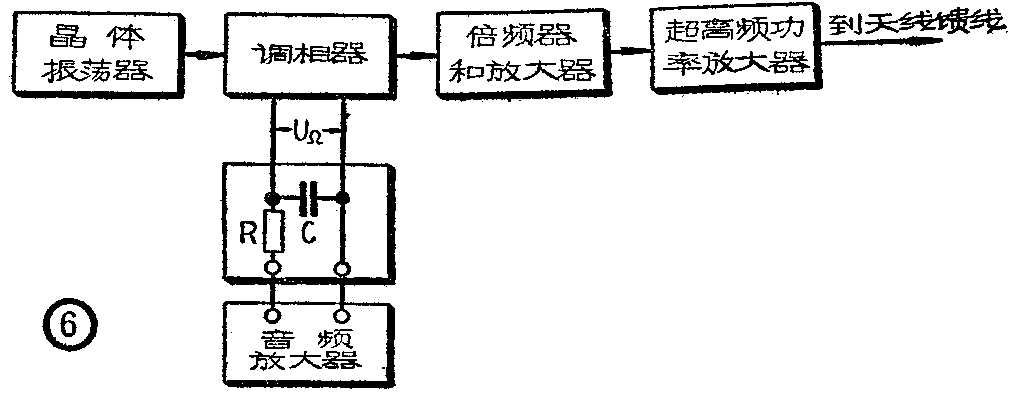
间接调频发射机的原理方框图如图6所示。音频信号放大后经过图中所示的RC电路加到调相器上（图4、5中音频变压器的初级）。由于电容C的电抗随着频率的增加而减小，而电阻R值是与频率无关的，所以当输入的音频信号电压的幅度不变而频率上升时，在C上输出到调相器的电压U\(_{Ω}\)将降低。根据图1可知，调相时的最大相移△和调制电压的振幅成正比的。加了RC网络以后，调相的△随音频频率的上升而减小，而其相应的频率偏移△ωφ亦将随之下降，这就改变了调相时的频偏随调制频率增高而加大的特性。反之，当音频频率降低时，也同样能得到使调相频偏加大的效果。适当地选择元件，可以使得调相器输出的已调振荡的频偏与调制频率无关，这样，调相电路的输出就具有调频的性质了。所产生的调频信号再经过倍频、放大后，由天线发送出去。

直接调频的优点是线路简单，易于设计。但由于直接对高频振荡器进行频率调制，而某些影响频率的因素很多，因而中心频率稳定度较差。使用由调相转变为调频的间接调频法，就不需要用调制电压直接控制高频振荡器本身的振荡频率，而是控制振荡器输出以后的高频振荡的相位，然后再转变为调频，这就可以使用高稳定度的晶体振荡器，克服中心频率不稳定的缺点。在调频通信和广播发送设备中，频率稳定问题是很重要的，因此多采用由调相转为调频的间接调频发射机。（瑶琪）