在调整和测试收音机、电子仪器或放大器时,都需要送入一个标准测试信号。例如在调试收音机的高频部分时需要送入高频信号,频率范围通常在几百千赫到几十兆赫,一般是用电感和电容组成的所谓LC振荡电路来产生这样的信号。LC振荡电路加上放大电路和电源构成一个高频信号发生器,就能输出高频信号。此外LC振荡电路用在超外差式收音机中,也将产生我们所需要的本机振荡信号,用来和外来电台信号进行混频(参阅本刊1965年第10期“半导体管振荡电路”一文)。在调测收音机的低频部分时,就需要有低频的标准信号。由电阻和电容组成的所谓RC振荡电路就能产生低频信号,它的频率一般在20赫到20千赫之间。本篇将对半导体管RC振荡电路进行一些分析。
一、输入输出串接起来的二级阻容耦合放大器
图1示有两级共发射极阻容耦合放大器,输入端1—1′上加有信号电压U\(_{1}\),放大器的输出端2—2′上有被放大的输出电压U3。我们来分析一下U\(_{3}\)和U1的关系。假定在某一时刻U\(_{1}\)的极性刚好使正偏压减小,由于这是共发射极电路,发射结是处在正向偏压情况,当U1增加使正向偏压减小时,I\(_{e}\)和Ic都减小,集电极电流I\(_{c}\)的减小使得负载Rz1上压降减小,而电源正极到BG\(_{1}\)管集电极之间的电压是电源电压与负载Rz1上电压之差,故R\(_{z1}\)上压降减小的结果使得这个电压增大,从而使集电极电位对电源正极而言更负,这相当于在原集电极直流电压上加了一个负电压U2这部分电压就是BG\(_{1}\)的输出电压,它的极性与U1相反(图中箭头表示由正到负),即“相位”相差180°;同样U\(_{3}\)要比U2相位又差180°或时间上又落后了半个周期;因此U\(_{3}\)和U1的相位共差360°,或时间上差了一个周期,结果和U\(_{1}\)同相。经过BG1后U\(_{1}\)被放大了K1倍;U\(_{2}\)通过耦合电容C3加到第二级放大器被放大了K\(_{2}\)倍,得出输出电压U3,故:
U\(_{3}\)=K2U\(_{2}\);但U2=K\(_{1}\)U1,
∴ U\(_{3}\)=K2U\(_{2}\)=K1K\(_{2}\)U1
=KU\(_{1}\)。(K=K1K\(_{2}\))
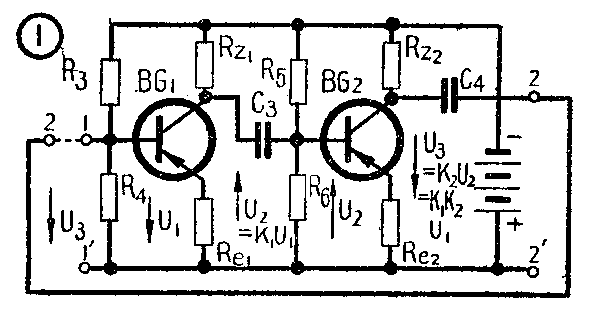
式中K是二级放大器总的放大倍数。
结果U\(_{3}\)的幅度比U1大了K倍。
如果开始时在放大器输入端加上电压U\(_{1}\),输出端就得到电压U3,这时再把2—2′和1—1′连接起来,U\(_{3}\)就加在输入端了。由于U3幅度比U\(_{1}\)大K倍,相位又和U1相同,其结果就等于把U\(_{1}\)加大一样,故放大器还是能照常进行工作,只是输出电压幅度更大而已,这时如把原来加入的输入电压去掉,放大器工作并不停止,它可以从输出端源源不绝地获得幅度足够大和相位相同的电压输入,就不需要外加信号电压供给,而由放大器本身产生,这就变为所谓自激振荡器。
实际上在开始时完全用不着外加电压U\(_{1}\),因为电路元件中电子固有的热运动,输入端总会有微小的各种频率的电压存在,其中某些频率电压就能作为原始的输入电压U1,如上述过程,振荡自会产生。可是象这种振荡器产生的波形和频率是怎样的呢?这是个重要问题。原来上面讨论时始终没有涉及到耦合电路元件C\(_{3}\)R6和C\(_{4}\)R4的作用。阻容耦合放大电路在比较宽的一般频率范围内是几乎不产生相移和衰减很小的(参看本刊今年第4期本专栏),因而U\(_{3}\)在较宽的频率范围内比起U1来幅度足够和相位相同,所以振荡器的振荡频率是很多的,故称多谐振荡器。既然它是由多种频率的正弦波所组成,当然不会再是正弦波了,而是类似于矩形波。我们把图1改画成图2的形式,可以很清楚地看出原来它就是常见的多谐振荡器的典型电路。
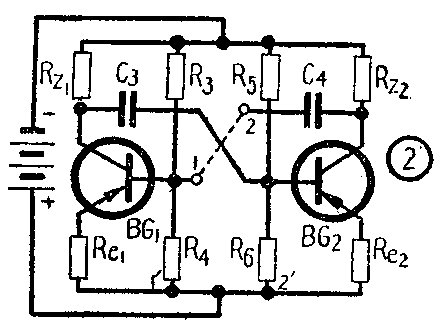
二、RC相移电路
二级阻容耦合具有正反馈的放大器不能获得单一频率的正弦波;如果加上一个附加电路,使得只有一个频率通过这电路输出,而且有比U\(_{1}\)足够大的幅度且和U1同相,让其他频率受到很大衰减和相移,使它们相对U\(_{1}\)来讲幅度又不够且不同相就不能振荡,这样放大器就在这单一频率上振荡而产生正弦波了。
这个附加的电路就是RC相移电路如图3,把这个RC电路的输入端接在放大器输出端2—2′上,因而加有电压U\(_{3}\);其输出就接在放大器输入端l—1′上而有电压U1,这时U\(_{3}\)和U1就不会在很多频率上相位相同而且幅度也不变。下面就简单分析一下原因。
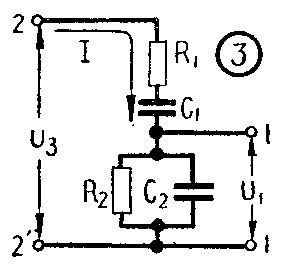
设U\(_{3}\)的频率是可变的,由零开始逐渐增大。当U3是直流电压(频率为零)时,这时C\(_{1}\)开路,全部电压降在C1上,故U\(_{1}\)为零。当U3的频率很低时,C\(_{1}\)、C2的容抗数值要比R\(_{1}\)、R2大得多(容抗=1/2πfC,C不变,f数值小时,分母小,容抗数值大),串联支路R\(_{1}\)C1阻抗很大,压降也大,但并联支路R\(_{2}\)C2因C\(_{2}\)容抗比R2大得多,故主要决定于R\(_{2}\),而R2比串联支路的阻抗小得多,因而U\(_{1}\)很小。随着U3的频率逐渐升高,C\(_{1}\)、C2的容抗逐渐减小,R\(_{1}\)C1上压降逐渐减小,故U\(_{1}\)渐增。再看U1和U\(_{3}\)的相位关系:当频率很低很低时,由于C1、C\(_{2}\)的容抗很大,R1比起C\(_{1}\)小得多可忽略,R2比C\(_{2}\)小得多,可认为C2被R\(_{2}\)短路近于不存在,而R2很小可忽略,因此整个电路可以看为近似只有电容器C\(_{1}\)存在。我们知道当一个电流对电容器充电时,开始一刹那电流最大,电容器因原先未充电,故开始时电压为零;以后电容器被充电,极板上电压逐渐升高而充电电流则逐渐减小,到最后电容器上电压达到最高数值,充电电流降到零。故电容上电压和流过电容器的电流数值变化是不一致的,即有所谓相位差;电流到最大时,电压为零。等到电流降到零时,电压才升到最高,故电流出现时间要比电压早上1/4周期,即相位上超前了90°。对照图3,当频率很低很低时,U3要比I落后了将近90°。但对于U\(_{1}\),因为C2容抗很大,相对于R\(_{2}\)可认为开路,所有电流通过R2,因为电阻上任何时刻电压电流都是一起增减的,故U\(_{1}\)和I相位相同。因此U1超前了U\(_{3}\)将近90°。
随着频率逐渐增高,U\(_{1}\)数值也渐增已如上述。同时因C2容抗逐渐降低,U\(_{1}\)相应也渐渐落后于电流I,超前U3的相角也就渐渐减小了。当频率增到某一数值f\(_{0}\)时,这时U3落后于I的相角和U\(_{1}\)落后I的相角相等,亦即此时U1和U\(_{3}\)同相,由于C1容抗的减小,这时U\(_{1}\)的数值也达到最大。这就是需要的振荡频率f0。
当U\(_{3}\)频率超过f0再升高时,C\(_{1}\)、C2的容抗更减小,使得相对于R\(_{1}\)、R2来说要小得多,此时因容抗减小对串联R\(_{1}\)C1支路上来说压降减小不多,但在并联R\(_{2}\)C2上,因C\(_{2}\)的容抗变小,旁路作用显著,使得U1随着频率增高而迅速降低。因为此时R\(_{1}\)、R2数值远大于C\(_{1}\)、C2电抗数值,故串联支路主要是电阻性,U\(_{3}\)落后于I的相角就愈来愈小;相反的,并联R2C\(_{2}\)支路,C2容抗远小于R\(_{2}\),大部份电流通过C2,C\(_{2}\)分路作用愈来愈大,使得U1落后于I的相角也愈增加,故相对的U\(_{1}\)落后于U3了,因为它落后于I的相角比U\(_{3}\)落后于I的相角还要大。
当频率很高很高时,C\(_{1}\)、C2可近似看为短路,U\(_{1}\)被C2短路故降到零,而相位上落后于I近90°了。此时整个电路近似只有电阻R\(_{1}\),故U3和I同相,因而U\(_{1}\)落后于U3近90°,U\(_{3}\)的全部电压几乎全降在R1上。
根据以上分析可知,只有在一个频率f\(_{0}\)时RC相移电路输出电压U\(_{1}\)和输入电压U3同相位,此时输出电压U\(_{1}\)最大。把这种RC电路接在放大器上,如果不考虑耦合电路的相位移,那么只有在f0上能产生振荡,也就是产生单一频率的振荡,放大器变成了RC振荡器。f\(_{0}\)叫做RC电路的准谐振频率,由RC电路的元件数值来决定,它等于
f\(_{0}\)=\(\frac{1}{2π}\)\(\sqrt{R}\)1R\(_{2}\)C1C\(_{2}\);
如果R\(_{1}\)=R2=R,C\(_{1}\)=C2
=C,则
f\(_{0}\)=\(\frac{1}{2πRC}\)。
把图2和图3合并就得到一个完整的RC振荡器的电路如图4。
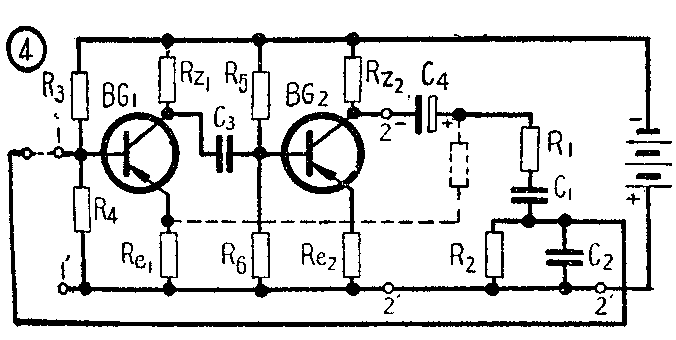
三、还得加负反馈
由于反馈回来的电压要比原来大得多,因为虽有RC反馈电路的衰减,但两级放大器放大倍数很大,因此振荡的振幅将不断增长,一直增长到半导体管输出特性的非线性区域,这时放大倍数迅速降低,一直到反馈电压和输入电压相等,振荡才宣告稳定。振幅的不稳定和讯速增长,一方面是使波形严重失真,另一方面对管子可能过载,甚至会损坏管子,因而需要添加入负反馈,以限制放大器的放大倍数。
在图4中,虚线表示接有负反馈。实用电路中在R\(_{el}\)处连接白炽灯泡以代替Rel,虚线电阻采用电位器以调整反馈量。当输入增大时,通过灯泡的电流变大,灯泡电阻增高,电流负反馈作用加强,放大倍数减小,遂起稳定振幅的作用。(苇杭)