实现调频的方法

在无线电通信和广播领域中，长期以来，都是采用“调幅”的方法来传递信息。但是，这种调制方式有它的缺点，如设备利用率低，抗干扰能力差，保真度不高等。采用“调频”方法，可以克服以上的缺点。但是它需要占用较宽的频带，要使用更高的无线电频率。随着超高频技术的发展，目前，“调频”已广泛用于高质量广播、电视，以及通信、雷达等设备中。

调频方法有两种。一种是直接调频法，它是用音频信号通过一个相当于电容或电感的元件——电抗管，直接控制高频振荡器的振荡频率。另一种是间接调频法，它是用音频信号控制高频振荡的相位，然后再设法转换为调频。本文先介绍采用电抗管的直接调频法。

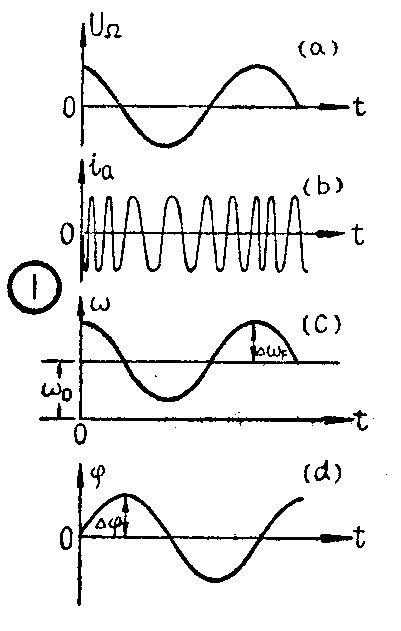
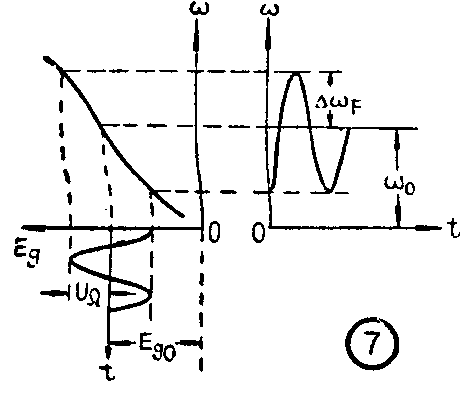
图1绘出调频时频率随音频信号而变化的情况。图中（a）是调制的音频信号电压（U\(_{Ω}\)）。（b）是高频电流（ia）的频率随调制信号电压而变化的情况。当调制信号为正半周时，振荡频率增高；而调制信号为负半周时，频率降低。对于不同的调制电路，频率随调制信号的变化情况也可能与此相反。图（c）表示出调频时频率（ω）随时间而变化的情况。ω\(_{0}\)是未调制前的振荡频率，称为中心频率。经过调频后频率变化的最大值ΔωF称为频率偏移或频偏。从图中可以看出，它是与调制电压的振幅成正比的。由于振荡的角频率ω（=2πf）也就是单位时间的相位变化率，例如振荡的频率是每秒1周，那么，它的相位每秒钟就要变化360°（2π），频率1000周，相位每秒钟就要变化1000个360°。因此在频率变化时，必然伴随着相位的变化；相位变化时，也必然伴随着频率的变化。所以调频振荡也伴随着有相位（ф）的变化，如图1（d）所示。这是调频振荡的一些基本特点。

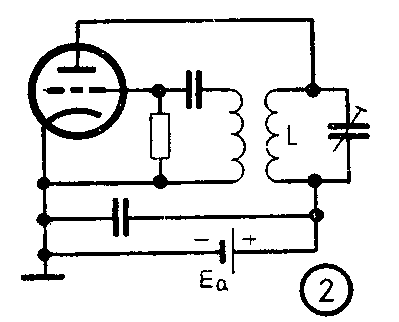
直接调频是怎样实现的呢？图2是用电感电容组成的自激振荡器。如果我们能够根据所要传送的音频信号有规律地改变振荡器的L或C，则振荡器的输出频率亦将按其规律作相应的变化，就能实现调频。可是，一般的电感和电容器很难完成这个任务。通常我们是用电子管通过一定的电路设计使它成为一个等效的电抗元件，接在振荡器的回路上（图3），这个等效电抗又能依着音频信号的大小而变化，从而实现调频。所用的电子管就称为电抗管。

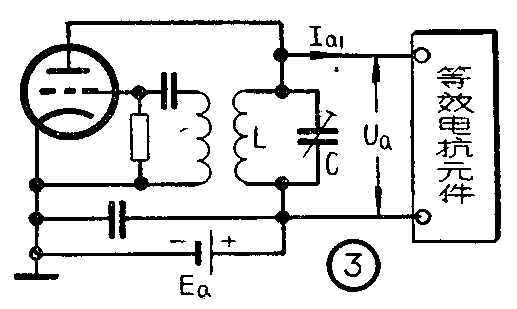
电子管怎样能等效于一个电抗元件呢？它的原理电路如图4所示。我们知道，流过电抗元件的电流与加在它上面的电压具有90°的相位差。如果电流超前电压90°则表现为容抗，落后90°则为感抗。因此，只要使图4所示电子管的高频电流I\(_{a1}\)能够与加在它屏—阴极间的高频电压Ua产生90°相位差，则从AB端看去，电子管将等效于一个电抗元件。从电子管工作情况知道，屏极的高频电流I\(_{a1}\)和加在栅极上的高频电压的相位相同。因此，要使电子管的Ua和I\(_{a1}\)获得90°相位差，只须设法使图4中的Ua和U\(_{g}\)相差90°就可实现。而电压Ua则是由振荡器供给的（参阅图3）。

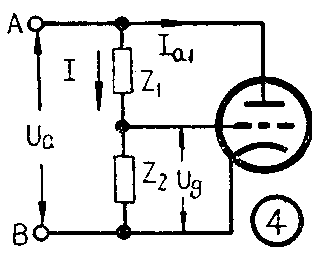
图4的Z\(_{1}\)和Z2就是用来使U\(_{a}\)和Ug获得相移的元件。它们按以下原则来选择：（Z\(_{1}\)+Z2）的数值较大，使流经移相器支路的电流不足以影响AB两端的等效电抗；Z\(_{1}\)值远大于Z2值，则支路电流I的性质取决于Z\(_{1}\)；此外，元件Z1和Z\(_{2}\)中的一个是电阻时，另一个必须是电抗。根据这些原则，可以设计出各式各样的移相器。这里我们只介绍两种典型电路。

图5a的Z\(_{1}\)为电容，Z2为电阻。根据上述原则，由于Z\(_{1}\)远大于Z2，移相器支路电流I的性质决定于电容C\(_{1}\)，因此是电容性的，它的相位超前Ua90°。此电流I在R\(_{2}\)上的电压降即为电抗管的激励电压Ug（=IR\(_{2}\)）。由于电阻上的电压降与流经它的电流同相位，亦即Ug的相位超前U\(_{a}\)90°。又因Ug与I\(_{a1}\)是同相的，结果，经过移相器的作用后，使Ia1的相位超前U\(_{a}\)90°。根据容性电抗的电流电压相位关系，此电子管将等效为容性电抗管。可用等效电抗XAB=U\(_{a}\)/Ia1=\(\frac{1}{ωC}\)\(_{AB}\)表示，其中CAB为电抗管的等效电容。

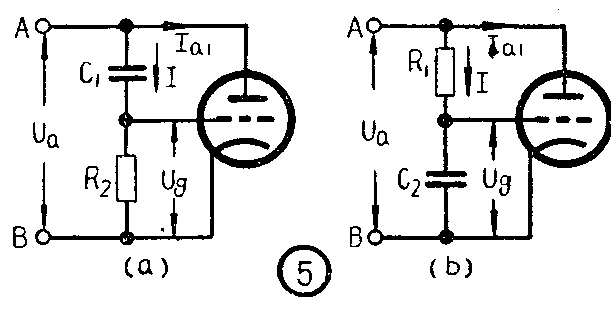
图5b的Z\(_{1}\)为电阻，Z2为电容。根据Z\(_{1}\)远大于Z2的同样原理，图5b的电流I决定于电阻R\(_{1}\)，为电阻性电流，与Ua的相位相同。而电容C\(_{2}\)上的电压降Ug（=IX\(_{c2}\)）的相位落后于I90°，也就是落后于Ua90°。而U\(_{g}\)与Ia1是同相的，所以电流I\(_{a1}\)将落后于电压Ua90°，电子管等效为感性电抗管。用等效电抗X\(_{AB}\)=UaI\(_{a1}\)=ωLAB表示，其中L\(_{AB}\)为电抗管的等效电感。

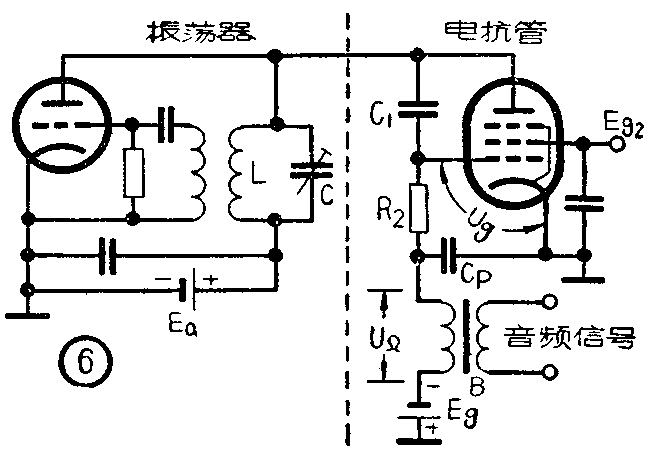
把电抗管接到振荡器的实用调频电路如图6所示。在实际应用中，电抗管常用五极管，振荡器用三极管或五极管。图中，采用屏极调谐的振荡器和容性电抗管联接。音频信号经过变压器B加到电抗管的栅极。电容C\(_{p}\)是把高频电流旁路到阴极，使Ug加于电抗管的栅—阴极之间。这样，电抗管栅极共加有三个电压；高频电压U\(_{g}\)，音频电压UΩ和栅偏压E\(_{g}\)。我们知道，当音频电压UΩ=0时，如果缓慢地改变电抗管的栅偏压E\(_{g}\)，它的高频电流Ia1就会发生变化。当栅偏压E\(_{g}\)增加时，Ial减小，E\(_{g}\)减小则Ia1增大。由X\(_{AB}\)=Ua/I\(_{a1}\)=\(\frac{1}{ωC}\)AB可见，在I\(_{a1}\)增大时，相当于等效电容CAB增加。反之，则相当于C\(_{AB}\)减小。而振荡器的回路并上了等效电容CAB后，当C\(_{AB}\)增大时（相应于栅偏压Eg值减小），它的振荡频率将降低。反之，振荡频率则升高。当加入音频信号电压U\(_{Ω}\)后，电抗管的栅偏压Eg将随着改变，从而使电抗管的等效电容以及振荡器的频率产生相应的变化，E\(_{g}\)和频率ω的变化关系如图7。通常把它称为静态调频特性。电抗管在工作时，只要适当地选择某一工作点Eg0，其所对应的未调状态的频率即为调频时的中心频率（ω\(_{0}\)）。加上音频电压后，该振荡器的输出频率将如实地反映出音频电压的变化规律。这就实现了调频。由图7可以看出，调频时的频偏ΔωF取决于调制电压的振幅大小。

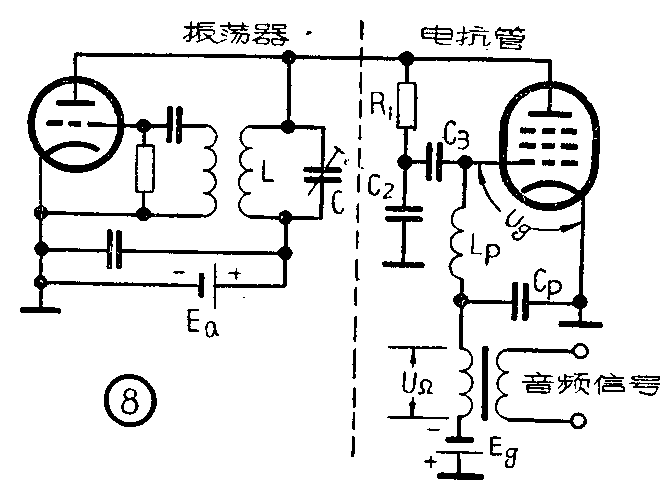
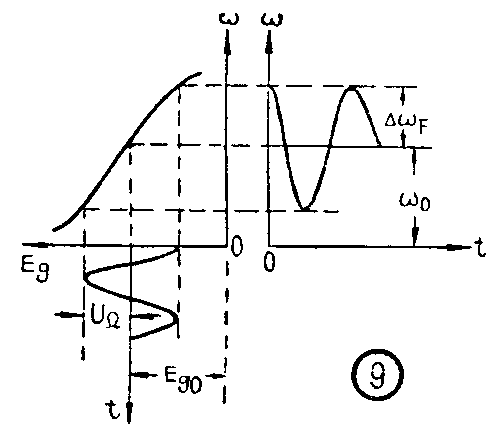
用感性电抗管的调频电路示于图8。高频电压U\(_{g}\)通过C3加在电抗管栅、阴极之间。C\(_{3}\)是隔直流高压电容器，不影响高频通过。电感Lp为馈送栅偏压E\(_{g}\)和音频信号用。根据同样原理，当栅偏压Eg增加时，I\(_{a1}\)减小，相当于等效电感LAB(由X\(_{AB}\)=UaI\(_{a1}\)=ωLAB）增加，使振荡频率下降。反之，则L\(_{AB}\)减小，而振荡频率上升。它的静态调频特性示于图9。

用直接调频的发射机方框图示于图10，音频信号经过音频放大器放大后加到电抗管上，控制振荡器获得调频信号输出。一般来说，振荡器的中心频率选得较低。因为降低振荡器的振荡频率将有利于提高它的频率稳定度。所以在已调信号之后使用了很多倍频器，把工作频率提高到超高频波段内，再用超高频功率放大器将已调信号放大到所需的发射功率。由于调频波的振幅是不变的，因此发射机的高频放大系流的电子管利用率很高，设备的效率也较高。

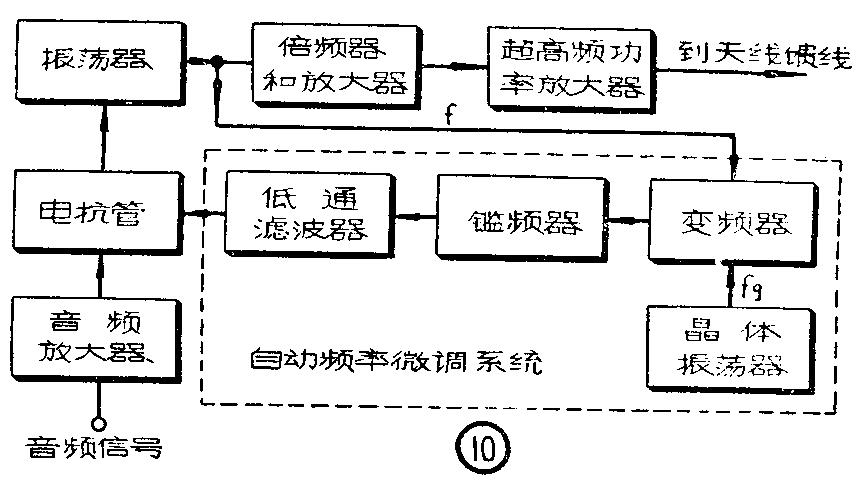
为了消除电源电压、电子管参量、外界温度等变化因素对振荡频率的影响，通常还应用了自动频率微调系统来进一步提高中心频率的稳定度。如图10虚线内所示。它的简单原理是，用一个频率稳定度较高的晶体振荡器作为参考振荡器，被调振荡器输出的频率为f的信号送到变频器中与晶体振荡器送来的频率为f\(_{g}\)的信号进行变频。变频器输出的差频（f—fg）信号加到鉴频器上，其输出电压的幅度随差频的变化而改变。当f等于预定的中心频率f\(_{0}\)时，则输出为零，当f偏离f0时，它将输出正的或负的电压。

如果把鉴频器的输出电压直接加到电抗管的栅极作为控制电压。并且连接的方向是，当频率f升高时，电抗管就控制振荡器使频率降低。反之，则使频率上升。这样，电抗管就可以使偏离中心频率的变化量变回很多。但是，振荡器的输出频率f不仅包含中心频率的偏移量，还包含正常的调制频偏，上述控制亦使有用频偏减小。为了消除中心频率的偏离而又不影响有用频偏，在鉴频器与电抗管间加入了低通滤波器。因为，一般来说，影响振荡器中心频率不稳定的因素，其变化要比调制信号的变化缓慢得多。因此，可以不让有用信号引起的变化通过低通滤波器，这就克服了自动频率微调系统对有用频偏的影响。（瑶琪）