在实际电路中,一般功率放大级多用推挽放大电路,它能够在失真较小的情况下,得到较大的输出功率和较高的转换效率。而推换放大器之所以能够作到这一点,主要是因为电路的对称性,能够抵消电子管放大器所产生的非线性失真。它的原理如图1所示。这种放大器要求放大器的两个电子管特性一样,并要求加到两个电子管栅极上的激励电压u\(_{g1}\),ug2是对称的(振幅相等,相位相反)。也就是说,当加到电子管G\(_{1}\)栅极上的电压处于正半周时,而加在电子管G2栅极上的电压处于负半周,两者相位相差180°,振幅要保持相等。
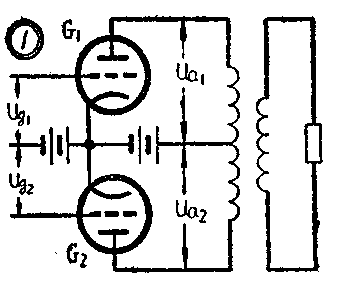
这就给我们提出了一个问题,如何得到这样的振幅相等和相位相反的两个对称电压,用来推动推挽电路。
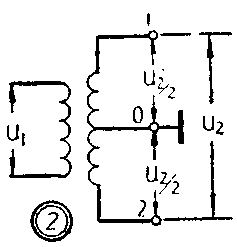
要获得这样的电压,实际上并不困难。我们做一个图2所示的变压器,令其次级线圈有一中心抽头即可。如果我们在初极侧加上一个交变电压u\(_{1}\),那么,在次级就感应一相应的交变电压u2。在某一瞬间,我们假定次级线圈的1端为正,2端为负,亦即端子1上,有一个对0端为正的电位u\(_{2}\)/2,在端子2上,有一对0端为负的电位-u2/2。两者之间,振幅相等,而相位相反。
现在我们把这个变压器接入如图3所示的电路,变压器的初级作前级放大器的负载,次级的两端分别接到推挽放大器的两个管的栅极上,中心抽头接地。当前级有交流信号时,在次级就得到两个对地振幅相等,相位相反的激励电压,加到推挽放大器的两个栅极上。这样就满足了我们上面所提出的要求。这就是用变压器把放大器从单端转换成推挽的电路。
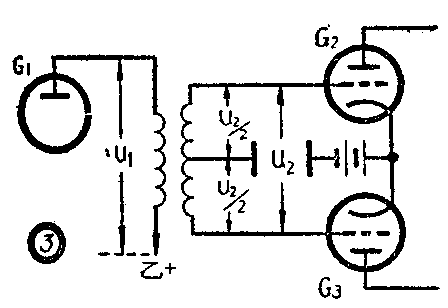
但是,由于变压器电路具有价贵和频率特性不佳等缺点,一般在小功率推挽放大器上,用得较少。另外人们还研究出一些利用阻容耦合方法来实现推挽激励的电路,即所谓倒相电路。
倒相电路的种类较多,我们只就倒相电路的原理,介绍几种简单的倒相电路。
分负载倒相电路
这个电路是把电阻耦合放大器的负载电阻,分成相等的两部分。如图4,一部分R\(_{1}\)接在屏极电路中,另一部分R2接在电子管的阴极电路中。这两个电阻的中点是地电位(通过电源),因此叫作分负载倒相电路。
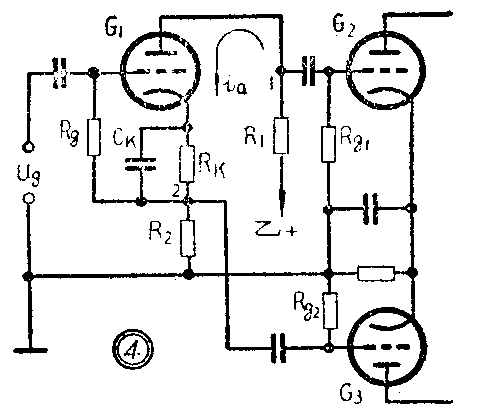
当加在G\(_{1}\)栅极上的信号电压为正的一瞬间,电子管的屏流(指交流成分,以下同)ia的方向如图所示,这个电流流过R\(_{1}\)时,使得R1上1点对地的电位是负的,即输出信号与输入信号之间的相位相反。但是接在阴极回路中的电阻R\(_{2}\)上的电压却不然,当栅极上有正信号电压时,流过R2的i\(_{a}\)使得R2上2点对地有一正电位。反之,当G\(_{1}\)栅极上的信号电压为负时,R1上1点对地的电位为正,而2点对地为负。因而,2点与1点对地的电位总保持相位相反。我们把1点的电信号通过耦合电容接到推挽放大级G\(_{2}\)的栅极上,把2点的信号,通过耦合电容接到G3的栅极上,那么,在这两个栅极上就出现相位相反的激励电压。由于R\(_{1}\)和R2相等,两个电压的振幅也相等。这样,就满足了推换放大器所提出的要求。
但由于电阻R\(_{2}\)是G1的阴极输出电阻,呈现在R\(_{2}\)上的输出电压,同时又是该电子管的输入电压,于是R2上的交流信号电压通过地端加到它自己的栅极上,形成负反馈。这个反馈电压又是整个放大器输出电压的一半。因而这是一个很深的负反馈,使电路的放大倍数大大降低,不超过2倍。负反馈,深的电路有一个比较重要的优点,它有较好的传真度,即使是在栅极上有一个较大的负偏压,使得倒相电路的工作点处在特性曲线的弯曲部分,负反馈也能消除由此而产生的非线性失真。
这种电路的缺点是:由于阴极和灯丝之间的分布电容,以及阴极电路和屏极电路的对地分布电容不同,这些电容对电阻R\(_{1}\)及R2上的电压起着不同的旁路作用,因而,在高音频时,两电阻上的电压不再相等,破坏了输出电压的对称性。
虽然有上述缺点,由于它有较深的负反馈,而减小了失真,电路也比较简单,再加上只是在高音频时,不平衡现象才显得严重,而在一般情况下,并无严重影响,所以目前这种线路应用得还比较广泛。
分压式倒相电路
上述电路美中不足之处,是对电压放大倍数的影响特大。我们现在介绍一种放大倍数较大的、叫做分压式的倒相电路。这种电路由两个电子管组成,如图5。电子管G\(_{1}\)用作一般放大,叫作放大臂,电子管G2用作倒相,叫作倒相臂。
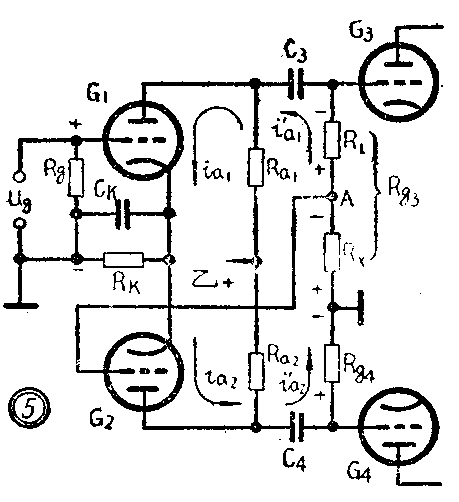
当输入信号电压处于正半周时,电子管G\(_{1}\)的栅极上有正信号,由于放大器的输出电压与输入电压的相位恰好相反,因此在电子管G3栅极上出现一负电压,也就是在电阻R\(_{g3}\)上对地而言有一个负电压。把G1的输出电压从R\(_{x}\)的上端A点处抽出一部分加到电子管G2的栅极上,于是,加在G\(_{2}\)栅极上的电压也是负的。这个电压经G2放大后倒相180°,所以G\(_{2}\)屏极上有一正信号电压。因而,G4栅极输入电阻R\(_{g4}\)上对地而言有一正电压,它与Rg3上的电压的相位恰好相反。于是我们就得到了两个相位相反的电压。
如何使这两个相位相反的电压保持振幅相等呢?也就是怎样来决定分压电阻R\(_{x}\)的大小呢?
R\(_{x}\)的阻值是由电子管G2的放大倍数决定的。假如R\(_{g3}\)上的电压是34伏,电子管G2的放大倍数又等于34倍,为了使R\(_{g4}\)上的电压也等于34伏,必须给G2的栅极加上1伏的电压,也就是等于R\(_{g3}\)上的电压的\(\frac{1}{34}\)。因此Rx应为R\(_{g3}\)的1;34。如果R1为33KΩ,R\(_{x}\)应为1KΩ。
这种电路没有像分负载倒相电路那样的负反馈,因而保持了较大的放大倍数,可得到较大的输出电压。
但由于增加了一个倒相臂,不可避免地,在交连电路以及极间存在着分布电容,这些电容必然使音频的高频段产生相移,于是就产生了不平衡现象和引起失真,这种现象越是在高音频,就越显著,因此这种电路也不可能在整个工作频段内保持平衡。
自动平衡式倒相电路
这种电路是分压式倒相电路的改进,电路基本相同,也分为放大臂与倒相臂两部分。它和分压式倒相电路的主要区别是,增加了一个自动平衡电阻R\(_{自}\),如图6所示。
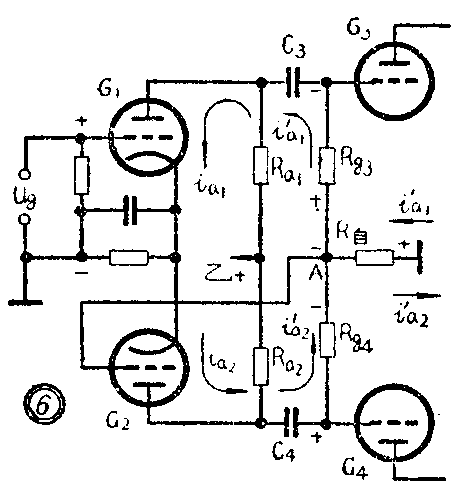
下面我们分析一下R\(_{自}\)是怎样起自动平衡作用的。
当输入信号为正时,电子管G\(_{1}\)的屏流,从G1的屏极到阴极入地后经由两条通路回至屏极,一条是经过R\(_{a1}\),另一条是经过R自、R\(_{g3}\),耦合电容C3,如图6所示。这时的信号电压地端为正,A点为负。由于电子管C\(_{2}\)栅极上的电压是从R自上抽取的,此时栅极上电压为负,这是因为它的屏流方向如图6所示。从图中可以看出,屏流的一条通路是经过C\(_{4}\),Rg4,R\(_{自}\)入地,它流过R自的方向和i′\(_{a1}\)相反。由于这两个电流以相反的方向流过R自,就起着相互抵消的作用。当i'a1较大时,则加到C2栅极上的信号电压就增高,于是i′\(_{a2}\)也增大,抵消了i′a1的增加。反之,当i′\(_{a1}\)减小时,加到G2栅极上的信号电压也必然减小,于是i′\(_{a2}\)也就减小,只保持R自上的电压不致减小,这就自动维持了G\(_{1}\)和G2两管输出电压的基本平衡。图5中G\(_{2}\)的屏流i′a2是经R\(_{g4}\)直接入地,不流过Rx,因而不能起到这种平衡的作用。
这里应该指出的,是R\(_{自}\)上的电压幅度绝不能等于零。若R自上的电压等于零,则G\(_{2}\)栅极上的输入信号就等于零,C2的输出也等于零了。从理论上讲,只有在R\(_{自}\)上的电压等于零时才是真正的平衡,所以这种电路不能作成真正平衡的。为了保持R自上有一部分电压,我们必须调整R\(_{g3}\)和Rg4,使其存在一些很小的不平衡现象。R\(_{g4}\)比Rg3约小6%左右。R\(_{自}\)的数值一般取相当于Rg3或R\(_{g4}\)的一半即可。
由于有一部分电压在R\(_{自}\)上互相抵消,所以放大倍数受到一些损失。
但由于这种电路能自动保持平衡,调整起来比较方便,电路也比较简单,所以目前应用较广。(琳田)