低频演示振荡器

将电容器和电感线圈如图1这样连接起来，就组成了一个振荡电路。利用这个电路，可以产生方向和大小随时间成周期性变化的电流，即振荡电流。在无线电教学中，通过演示，让同学们直接观察到振荡电路的工作现象，对于理解振荡电流的产生，很有帮助。

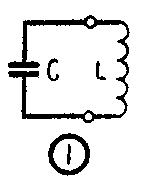
利用电感量很大的铁心线圈和电容量很大的电容器，能够制成通过大型电流计指针的摆动而显示出振荡电流的低频振荡器。利用它可以观察阻尼振荡和无阻尼振荡的产生，以及振荡电流的周期（或频率）跟电容和电惑之间定性和定量的关系。

低频演示振荡器的制作，为要达到演示的良好直观效果，必须具备以下两个基本条件：第一，铁心线圈的电感量要在千亨以上，电容器的容量须为数十微法。由于振荡电路中的振荡电流是要求通过大型电流计指针的摆动而显示出来，那么振荡电流的周期应该相当大才行，一般须接近一秒或一秒以上。根据振荡电流周期的公式，T=2π\(\sqrt{LC}\)，式中L为电感量（单位亨），C为电容量（单位法拉），T为周期（单位秒）。如果要得到1.8秒的周期，当电容量为70微法时，根据上式可以算出电感量大约要1200亨。第二，要线圈和电容器组成的振荡电路能够起振荡，电路的直流电阻（R）和电感（L）电容（C）之间，必须满足

的关系，在制作中要求直流电阻R愈小愈好。

从以上条件出发，制作低频演示振荡器关键在于铁心线圈的制作和电容器的选择。大电感量的铁心线圈，通常无成品可以代用。一般的变压器，铁心小的线圈圈数多，铁心大的则圈数少不能得到所需要的大电感量。为此，必须要自己动手绕制。要得到大电感量的铁心线圈，除了要采用导磁率较大的硅钢片和较大的铁心横截面以外，最有效的方法是增加线圈的圈数，因为电感量和线圈圈数存在着平方正比的关系。为了使线圈圈数加多，而又减小直流电阻，铁心的窗口空间就要求大一些，用线线号要求小一些。一般采用□字形铁心（图2）较为适宜。如果采用截厚面积=1时×2\(\frac{1}{2}\)寸，c=1寸，b=31;8寸，a=338寸的□字形铁心，用0.38毫米（28号）的漆包线绕16,000圈，电感量就有一千多亨，而直流电阻却不到一千欧。

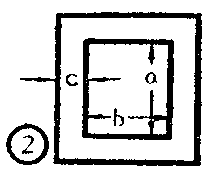
如何绕制线圈呢？先用薄板胶合好两个线框，大小要能刚好套进铁心。绕线时，须注意使绕线紧、匀、密、平。每绕一层对两头的线圈最好涂以快干胶，及免向外松脱，并且线圈层间隔以绝缘的蜡纸。当两个线圈各绕到\(\frac{3}{4}\)处抽出一头，以便作改变电感量和反馈线圈之用，反馈线圈一般是总线圈圈数的1;4～13。

线圈绕成后，可以用电流电压法测定它的电感量。测的方法是：用一降压变压器得到10～20伏50赫的交流电，加在铁心线圈的两端，用交流亳安表测出电流，交流电压表测出电压，用万用电表测出直流电阻，再用公式

式中的V是电压（单位伏），I是电流（单位安），R是电阻（单位欧），f是频率（50赫）。

电容器最好采用无极性的，例如日光灯上用的纸质电容器。如果没有这种电容器，也可采用质量好的电解电容器数个并联。虽然电解电容器正反方向的电容量和漏电电阻不同，但只要质量是好的也可以用。

有了大电感量的线圈和大容量的电容器后，就可动手设计振荡器了。图3是常见和最容易起振的三点式（哈脱莱）振荡线路。振荡器由6N1双三极管的一部分和L、C组成，通过阴极反馈能量，以维持振荡的持续进行。L、C振荡电路中的振荡电流通过一只大型电流计CB（0—1毫安或0—3毫安）指针的摆动显示出来。为了使振荡稳定和避免栅流影响指针摆动的不对称性，特在栅极上加上一个由8—20微法电容和2兆欧电阻组成的栅漏，并把电流计连接在如图3所示的位置。为了使线圈的电感量和电容器的容量能够变更，线圈和电容器均备有外接抽头，通过单刀双掷开关S\(_{1}\)，S2进行控制。单刀双掷开关S\(_{1}\)是在进行阻尼振荡实验时接通和切断B电源与L、C振荡电路之用。

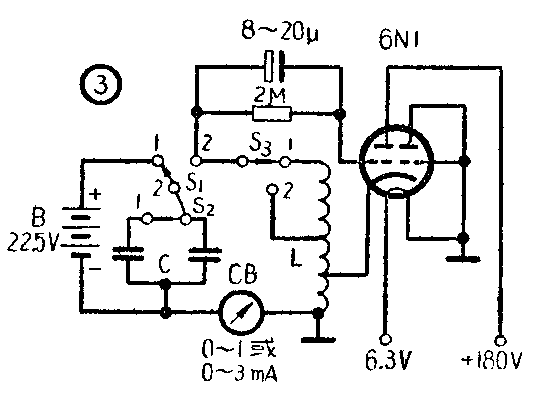
利用这个低频演示振荡器可以进行以下实验：

1．阻尼振荡的演示

演示时，用导线将实物照图3线路连接好，不接通交直流电源，而将开关S\(_{1}\)，S2，S\(_{3}\)都掷到1位置，此时B电源对电容器C充电。待数秒钟后将开关S1掷到2位置，充了电的电容器则对线圈L放电，电流计的指针则减幅地摆动数次而停下来。如果CB用阻尼较大的小型电流计，充电电压只能用3～4.5伏，所能观察到的摆动次数较用大型电流计的为多。

在上述实验里，电流计指针的摆动是由真正的电振荡而引起，还是由于指针摆动的惯性而引起，通常鉴别的方法有二，其一，改变电感量或电容量，看电流计指针摆动的快慢是否改变。例如将开关S\(_{2}\)，S3分别掷到2位置时，如果指针的摆动变快，就可证明是由真正的电振荡而引起的摆动。其二，当指针偏向一方后立即切断L与C的电路，等指针回到零位置后，再接通L，C电路，此时，如果指针向另一方摆动（即反向放电），则可证明是有真正的电振荡产生。

2．无阻尼振荡的演示

演示时，将开关S\(_{1}\)掷到2位置后，接通电子管工作的电源，这时可见到电流计的指针，逐渐地摆动起来，很快达到稳定状态，等幅地振荡起来。

3．振荡电流的周期跟电感量、电容量之间的关系

第一，定性观察。在无阻尼振荡演示基础上，将开关S\(_{3}\)掷到2位置时，由于L减小，则见电流计指针的摆动变快即周期变小。然后，将开关S3又掷到1位置再将开关S\(_{2}\)掷到2位置时，由于C减小，则见电流计指针的摆动也变快即周期也变小。由此可见，振荡电流的周期是随L、C的减小而减小，随L、C的增大而增大。

第二，定量分析。在实验时，线圈共有16,000圈，每个线圈为8000圈，电容器是选用日光灯上所用的电容器15只分成三组并联而成，每只电容器的容量是4.75微法。实验所得定量的数据如下表：

从以上定量分析实验可知：振荡电流的周期（T）和电感量（L），电容量（C）的平方根存在着正比关系。（盛孝官）