半导体管常用参数的测试

我们用一些特定的参数来表示各种不同种类不同型式的半导体管的特点和质量好坏。由于制造方法、工艺过程、使用范围及应用状况不同，半导体管的特性参数分有：直流参数（包括直流极限参数）、低频参数、器件参数、高频参数（包括超高频特性参数）、频率特性参数、开关特性参数等多种。全面介绍这些参数是很复杂的，而且对一般应用来说也不必要。这里将着重介绍几种常用参数的测量原理和测量方法。

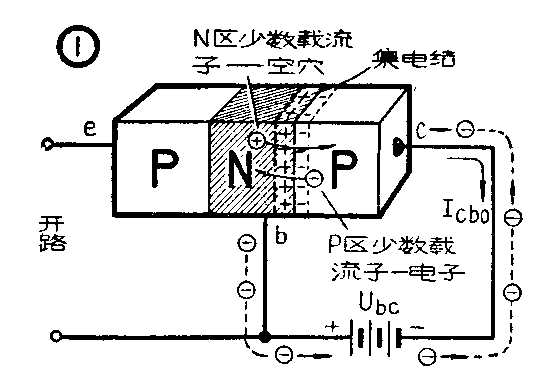
I\(_{cbo}\)表示当发射极开路，在集电极（c）和基极（b）之间加以一定的直流电压Ubc时，流过集电极的电流，简称为集电极反向截止电流（以前曾称为反向饱和电流）。直流电压的加接必须使集电极一基极间呈反向偏压的极性：对P－N－P型三极管来说，集电极接负压；基极接正压。由于集电结中内电场的阻挡作用，使得P型区的多数载流子（空穴）和N型区的多数载流子（电子）都难以向对方扩散，但这时集电极的内电场却非常有利于双方的少数载流子（P型区为电子，N型区为空穴）的扩散（见图1）。在一定的温度下由于热运动而产生的少数载流子的数目是一定的，与加接的反向电压U\(_{bc}\)的大小无关，因此，我们就称这种集电结少数载流子所形成的电流为集电极反向截止电流。所谓“反向”，即表示是在反向电压下呈现的；“截止”是表示这一电流不再随电压的增大而变化的意思。应该提醒的是：实测出来的Icbo包含了反向饱和电流以及一部分跨在P－N结上的漏电流I\(_{s}\)；前者与电压大小无关，后者却与电压Ubc有关，大体上服从欧姆定律。

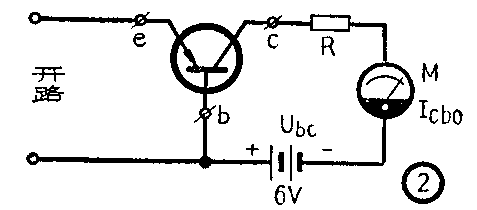
I\(_{cbo}\)的测量原理见图2。电池电压为6V。M可用500型万用表之50μA直流电流档，电路再串接一个阻值为200千欧的电阻（R），以防止联接错误或半导体管有缺陷等反常情况而造成事故。当如图插入半导体管后，表上的读数即为所测之Icbo。

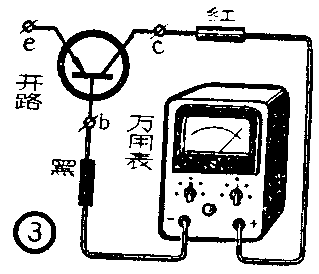
如果手边没有50μA档的万用表，可按图（3）方法测定集电结反向电阻的大小。万用表应拨至R×1,000档；“＋”试笔与“-”试笔切不可接反。这个阻值对一般小功率管而言，为几百千欧，越大越好，如果太小则表示I\(_{cbo}\)太大，就不宜使用。

I\(_{cbo}\)(在一些旧特性表中称为Ico）的大小，既表征半导体管的完好与否，也表示管子在工作时的稳定情况。一般小功率管的I\(_{cbo}\)在1～10μA之间，而硅三极管的Icbo不得大于锗管的1/10；大于这个范围的管子稳定性差。如果I\(_{cbo}\)为无穷大，表明集电极和基极间短路了，若Icbo等于零，则说明上述电极开路。

I\(_{cbo}\)随温度的变化很灵敏，每当集电结的温度增加10℃时，Icbo将增大1倍，换句话说，假如某一管子在25℃时I\(_{cbo}\)为2μA, 则在75℃时将为64μA，从而使得工作点不稳定，并导致放大性能也随温度变化。因此我们在选择管子的时候，应尽量选取Icbo小的。由于I\(_{cbo}\)中还包含了一部分漏电流Is，它与U\(_{cb}\)成正比，因此在一些简单的半导体管电路中，可以选取较低的偏压（例如用1.5或3伏），也可以减弱Icbo的影响。

I\(_{ceo}\)表示当基极开路，集电极（c）至发射极（e）之间加以反向偏压Uce时，流过集电极的反向截止电流，简称“反向穿透电流”。根据分析可知，I\(_{ceo}\)与Icbo的关系为：I\(_{ceo}\)=Icbo（1＋h\(_{FE}\)），其中hFE是共发射极工作时的直流电流放大系数，因为h\(_{FE}\)比1要大得多，故可以近似地认为Iceo=I\(_{cbo}\)×hFE，因此I\(_{ceo}\)比Icbo要大很多倍。又因为I\(_{cbo}\)和hFE都与温度有关，所以I\(_{ceo}\)对温度是极敏感的。在实际应用中多数采用一组电池供电的共发射极电路，因此Iceo可以更实际地表示出管子工作于共发射极电路时的稳定性。

I\(_{ceo}\)的测量电路如图4所示，保护电阻R为5～3千欧的碳膜电阻，M为任一型号的万用电表，量程可拨至直流“1mA”档上，插上被测管后，表的读数即为Iceo。

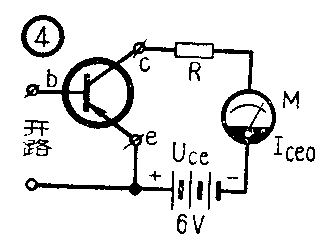
小功率管I\(_{ceo}\)（亦称Ido）之数值一般在500μA以下，数+μA的管子则较为理想。如果I\(_{ceo}\)超过2mA，则集电结已击穿了。如Iceo为零，则表明发射极或集电极已脱焊或断裂。

如果没有条件进行图4的测量，亦可按图5的方法测量发射极与集电极间的电阻，不过一定要特别注意极性不能接反，否则将会使管子烧毁。这样测量时，性能正常的管子表头读数一般不小于50千欧，过小就表明I\(_{ceo}\)很大，就难以稳定地工作。

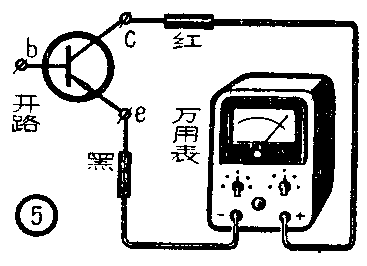
以上关于截止电流的测量方法，均指P-N－P型管而言，如系N－P－N型管则电池和仪表的正负极性均应对调一下。

在半导体管的反向伏安特性中，发现当电压加大到某一数值时，反向截止电流会突然急剧地增加，这种现象称为“击穿”现象（见图6示）。如果电流增加非常迅速则称为“硬”击穿，缓慢增加则谓之“软”击穿。实验证明：击穿现象的产生是由于在强电场的作用下半导体内自由电子数目增多，或载流子获得足够高的能量，碰撞出新的自由电子所形成。

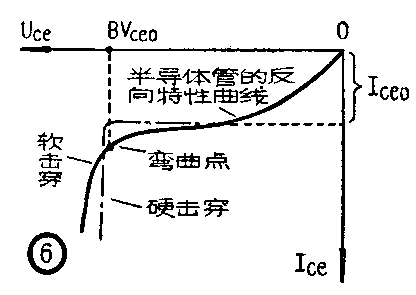
实际测量是当基极开路时，增大加接在集电极与发射极间的反向电压，使集电极截止电流达到某一规定值时，对应的集电极至发射极反向电压即为共发射极击穿电压，并以符号BV\(_{ceo}\)来表示（图6曲线弯曲点对应之电压即为BVceo）。

击穿电压BV\(_{ceo}\)是表示集电极与发射极间所允许加的最大极限反向电压，为半导体管直流极限参数之一，它给出了半导体管直流工作电压的安全区域。工作电压超过BVceo的数值，管子便会击穿损坏。

BV\(_{ceo}\)的测量有图示法和恒流法两种：前法可以直观地看出反向曲线及击穿性质，但线路较为复杂；后者测量简便，读数迅速，但就业余条件而言装一个完善的恒流源比较困难。这里介绍一种简便的恒流测量法供作参考。按照图7的电路进行测量：调节R1及R\(_{2}\)，使电路流通规定的电流，此电流之大小要求不一，但对一般常用的小功率三极管而言为1mA，并由M1加以指示，则此时M\(_{2}\)的电压读数就是所测之BVceo。M\(_{1}\)及M2可以用一块万用表先后测量，开始时断开K,将万用表拨至直流1mA档，并串接在电路中，闭上K,当电流调到1mA后，可将万用表取出，并拨至50V直流电压档，并联在集电极与发射极间，并注意将ab两点联接起来，这时万用表的读数便是BV\(_{ceo}\)。

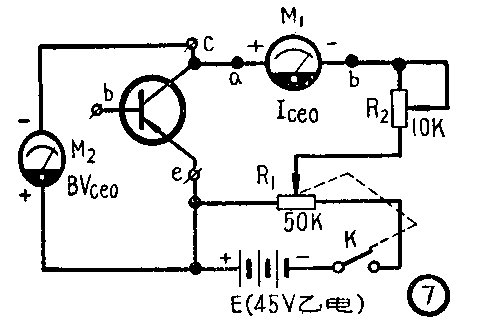
一般小功率管的BV\(_{ceo}\)均在（15～30）伏上下。当M2所指示的电压低于15伏，表明质量不好，因为随着温度的升高， BV\(_{ceo}\)会下降的。若M2指示的电压在5伏以下，则表明管子已接近击穿或已击穿而无法使用了。在一些特性表中往往只给出BV\(_{cbo}\)（共基极击穿电压）的数值，它与BVceo有着|BV\(_{cbo}\)|＞|BVceo|的关系。因此，在作共发射极使用时，应采用比BV\(_{ceo}\)更低的偏置电压。在收音机电路中由于一般电源电压为6V，故没有击穿的危险，但在其它电路却要特别注意，所选取的工作偏置电压，应不大于BVceo的（0.7～0.8）倍，以免产生热电击穿。

β表示半导体管工作于共发射极电路情况下，当负载对交流短路时，输出交流电流i\(_{c}\)与输入交流电流ib之比。由于半导体管是一个电流放大元件，其放大性能的好坏是通过短路电流放大系数β值的大小来表征的，因此β也是常用的基本参数之一。由于电流放大系数β随输出端负载大小而改变，因此只有当负载“短路”时，才能更合理的表明半导体管自身（不因负载影响）的放大性能。输出短路是利用一个容量很大的电容器C旁路交流来实现的（见图8）。

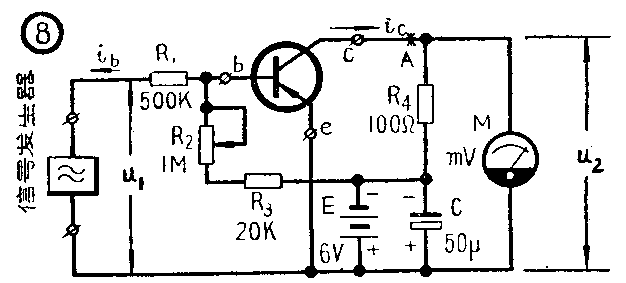
一般说来β值越大，则放大性能越好，但β太大了工作性能就很不稳定，所以β值在25至100间都是较好的管子。

在一般特性表中常有用符号h\(_{21}\)或hfe、α\(_{cb}\)来表示短路电流放大系数的，它们都具有与β相同的含义。但也有些特性表中只给出α的数据。α为共基极的电流放大系数，它与β具有β=α／（1—α）的关系，因此当给出α的数据后，也就可以获知β的大小了。

β值是受直流工作点影响的，因此改变直流工作点，往往就可以获得改善管子放大性能的效果。此外，在不同的频段中β值不同，因此有高频管与低频管之分；但每一种半导体管都能正常地工作于某一定频段内，在此段内β值基本上没有什么变化。

β的测量原理如图8示，因为β=\(\frac{i}{_{c}}\)ib；i\(_{c}\)R4=u2,i\(_{b}\)R1=u\(_{1}\),(因R1>>被测管之输入阻抗），故i\(_{c}\)=u2/R\(_{4}\)；ib=u\(_{1}\)/R1,则有下式：

将跨接在输入端的信号发生器的频率调到1千赫上，并调节其输出电压使u\(_{1}\)=5伏，R1=500千欧，R\(_{4}\)=100欧，代入（l）式可得：

u\(_{2}\)是用电子管毫伏表M测出，如将M的量程置于100毫伏档上，则M指示满刻度时对应β值为100，即毫伏数与β数值相对应。这样，我们就可以从毫伏表的刻度上直接读出半导体管的β值来。图8中之R2为调节直流工作点的电位器，E为6伏干电池，C为50（或100）μF的电解电容器，旁路交流用的。在图中A点可监视直流工作电流I\(_{c}\)，在测量前可断开A点串入一万用表（量程放在直流1mA档），调R2使万用表指在1mA上即可。此法测β较准确，但须用信号发生器及电子管毫伏表等设备，对业余爱好者说来是较困难的，因此下面再介绍两种测直流电流放大系数h\(_{FE}\)的简便方法。

1）由于I\(_{ceo}\)=Icbo（1＋h\(_{FE}\)），因此我们只要用上述测Icbo及I\(_{ceo}\)的方法测出Icbo及I\(_{ceo}\)，便可简便地按上式算出hFE来。

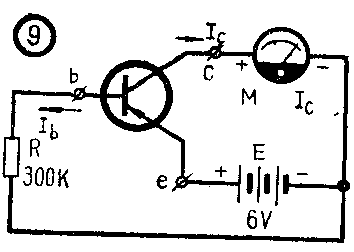
2）可用图9的原理进行h\(_{FE}\)的直接测量：由于R》发射结的正向电阻，故Ib≈E／R=\(\frac{6}{300×10}\)\(^{3}\)=20微安，而I\(_{c}\)则由M直接加以指示。M系一万用电表的直流电流档（1mA或5mA档）。把Ib和I\(_{c}\)值代入hFE=I\(_{c}\)/Ib便可得出所求的数据。一般h\(_{FE}\)= (0.8～0.9)β, 所以测出hFE便可近似地估出β来。

h\(_{ie}\)表示半导体管工作于共发射极情况下，当输出端短路时的交流输入电压ube与输入电流i\(_{b}\)之比值，我们就把这个比值称为半导体管共发射极输入阻抗，即hic=\(\frac{u}{_{be}}\)ib。输出短路亦由一容量很大的电容器C对交流旁路而加以实现。

h\(_{ie}\)也是半导体管常用参数之一。因半导体管在实际运用中大多用来作为放大或振荡元件，因此要考虑放大级的阻抗匹配、输入阻抗、变压器匝比、振荡回路计算，以及更换半导体管等等情况，这些均与hie有关。 h\(_{ie}\)与直流工作点、负载、频率均有关；而当频率、负载一定时，hie与集电极电流I\(_{c}\)成反比，因此，我们可以在一定范围内，通过调节Ic来改变输入阻抗的大小，从而达到改善级间匹配和减小失真等目的。h\(_{ie}\)的数值较分散，当Ic为1mA时，一般在400欧至5千欧的范围内。在特性表中往往只给出h\(_{ib}\)（共基极的输入阻抗），但可从hie=h\(_{ib}\)（1＋β)的关系式中算出hie来。

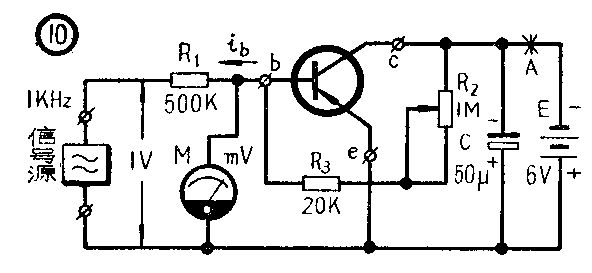
h\(_{ie}\)的测量原理图见图10示，它与β的测量电路很相似，除将R4取消并将电子管毫伏表M跨接在输入端外，余均相同。因R\(_{1}\)》半导体管输入阻抗，故ib=\(\frac{1}{500}\)×10\(^{－3}\)=2μA近似是一个常数，因此h\(_{ie}\)=ube／i\(_{b}\)=ube／2μA，故当u\(_{be}\)为10毫伏时，hie=5千欧，其余类推。

每次在测量时，必须首先将直流工作点调好以后方可进行。

上面已经谈到，半导体管的放大系数β随着信号频率的高低而改变，频率升高，β降低。f\(_{β}\)就是表征半导体管的放大性能随工作频率变化的参数，因此也称为频率特性参数。

设β\(_{0}\)=低频时（1千赫的工作频率下）的短路电流放大系数，则在其它频率下半导体管放大系数与频率的关系如下式：

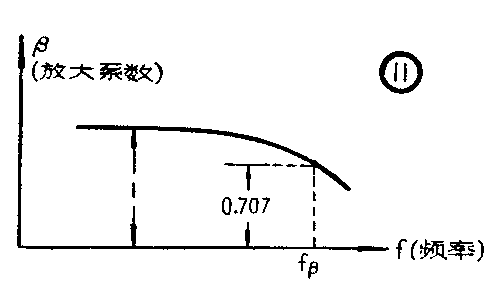
由（2）可知，当工作频率f<f\(_{β}\)时β≈β0，放大性能没有什么变化，而当频率升高到f=f\(_{β}\)时, 则有：β=1\(\sqrt{2}\)β0= 0.707β\(_{0}\)。因此fβ被定义为这样一个工作频率：在达到这个频率的时候，共发射极电路的短路电流放大系数β降低到低频（f=1,000赫）时数值的1;2（=0.707），参看图11。

不同型式的半导体三极管的f\(_{β}\)具有不同数值，例如合金型三极管（3AX1～3AX5）的fβ一般在（10～50）千赫上下，而扩散型三极管（3AG11～3AG14）则在（0.4～20）兆赫范围左右。对f\(_{β}\)的挑选要根据所应用的电路需要来具体决定，不必强求一律。但一般说来，在不考虑功率大小的情况下，管子的fβ越高越好在一般特性表中，往往只给出f\(_{α}\)（共基极截止频率）的数据，在频率不太高的情况下它与fβ的关系近似地有f\(_{α}\)=β·fβ。

对f\(_{β}\)的简单测量可以借助图8的电路进行，设在信号频率为1千赫时测出的β=A,升高信号频率，并保持信号输出幅度不变（例如固定为1伏），直至β=0.707A, 则此时所对应的信号频率数即为被测管的共发射极截止频率fβ。 (操申生）